
- •73. Свойство плотности распределения вероятностей св
- •77. Плотность распределения равномерного распеределения на отрезке
- •78. Плотность распределения показательного распределения
- •86. Свойства двумерной функций распределения вероятностей
- •89. Свойства двумерной плотности распределения вероятности нсв
- •92. Как найти маргиональные плотности по двумернй плотности распред св
- •93. Как найти вероятность попадания двумерной св в область d
- •94. Аналогично теоремы умножения
- •98. Формулы для расчёта мат.Ожидания. Одномерной дсв и нсв
- •100.Свойства м.О.
- •137. Мультипликативное свойство производящей функций
- •140. Формулы расчёта хф для нсв и дсв
- •141. Свойства хф
137. Мультипликативное свойство производящей функций
Если ζ1,.., ζi независимые целочисленные СВ, то хар-кая функция их суммы равна произведению хар-ких функций. ζ1.. ζn (s)= ζ1(s)… ζn(s)
138.
Можно ли производящую функцию считать
законом распределения и почему Коэф.
Рn
степенного ряда
ζ(s)=Msζ=
npn
одназначно опред как рn=(1/n!)*
nζ(0),
’ζ(s)=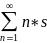 n-1pn=p1+
n-1pn=p1+
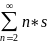 n-1pn
,
’ζ(0)=p1
и так далее. Т.о имея
ζ(s)
можно однозначно восстановить таблицу
распределения ζ
n-1pn
,
’ζ(0)=p1
и так далее. Т.о имея
ζ(s)
можно однозначно восстановить таблицу
распределения ζ
139.
Характеристическая функцией СВ
ζ
наз функция fζ(t)=M(eitζ)= itxdFζ(x),
t
R,
fζ(t)
C,
i=
itxdFζ(x),
t
R,
fζ(t)
C,
i=
140. Формулы расчёта хф для нсв и дсв
fζ(t)= itx
pk
,
itx
pk
,
fζ(t)= itxpζ(x)dx
141. Свойства хф
10. fζ(0)=1;
20. |fζ(t)| 1, t R
30. faζ+b(t)=aitb fζ(at)
40. | fζ(t+
)-
fζ(t)
|
| fζ(t+
)-
fζ(t)
|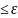 ХФ равномерно непрерывна на всей
числовой оси
ХФ равномерно непрерывна на всей
числовой оси
50. Если СВ ζ1,.., ζi независимы, то ζ1+.. +ζn (t)=Пi=1nfζ : (t)
60.
если
для к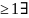 конечный момент к-го порядка, то
конечный момент к-го порядка, то
 непре-рывная производная к порядка от
Х.Ф и
непре-рывная производная к порядка от
Х.Ф и
 к=Мζк=(1/ik)*fζk(0)
к=Мζк=(1/ik)*fζk(0)
70.
если М|ζ|k<
, то в окрестности точки t=0
справедливо следующие разложения
fζ(t)=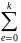 ((it)e/e!)
Mζe
+0(|t0|k)
((it)e/e!)
Mζe
+0(|t0|k)
80. fζ(t)= fζ(-t)
142. мультипликативное свойство ХФ.
Если СВ ζ1,.., ζi независимы, то ζ1+.. +ζn (t)=Пi=1nfζ : (t)
143. Как с помощью ХФ найти начальные моменты распределения к=Мζк=(1/ik)*fζk(0)
144. Можно ли ХФ считать законом распределения вероятностей Х.Ф. однозначно определяет функции Распределения согласно ХФ является законом распределения СВ
145. Как плотность распределения вероятностей восстанавливается по ХФ
pζ(x)=(1/2*Pi) -itxfζ(t)dt
146. Выводы о преимуществах использования ХФ
Использовать ХФ рекомендуется тогда, когда приходится иметь дело суммами независимых СВ в данном случаи по ζ1+.. +ζn (t)=Пi=1nfζ : (t). Найти распределения суммы проще, чем вычислять интеграл типа свертак для плотностей распределения.
147. Формулы для расчёта дисперсии в двумерном случаи
Dζ1=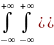 1-Mζ1)2pζ1ζ2(x1,x2)dx1dx2=
1-Mζ1)2pζ1ζ2(x1,x2)dx1dx2=
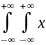 12pζ1ζ2(x1,x2)dx1dx2=(
12pζ1ζ2(x1,x2)dx1dx2=( x1pζ1ζ2(x1,x2)dx1dx2)2
x1pζ1ζ2(x1,x2)dx1dx2)2
