4. Оценка точности измерений

Интервальная оценка с помощью доверительной вероятности. Довери­тельный интервал это интервал значений х, в который попадает истинное зна­чение х_ист измеряемой величины с заданной вероятностью.

Доверительной вероятностью Рд называется вероятность того, что ис­тинное значение измеряемой величины X_ист попадает в данный доверительный интервал.

Задавшись величиной доверительного интервала от - ∆x до + ∆x , и проин­тегрировав выражение (5) в заданных пределах можно определить вероятность того, что случайная погрешность измерения не превысит ∆x .

(9)

Задав в качестве доверительного интервала ц пределы ±3 можно опре­делить вероятность того, что погрешность не превысит 3. Это правило «трех

сигм».

т.е. с вероятностью 99,73% любая случайная погрешность находится в пределах +3 от среднего арифметического значения.

Чаще всего доверительную вероятность Р_д принимают равной 0,90; 0,95; 0,9973. Обычно, при проведении технических измерений Р_д = 0,95. Квантиль нормального распределения (аргумент интегральной функции Лапласа) для Рд -0,90; 0,95; 0,9973 соответственно U_p =1,65; 2; 3 (таблица 1 приложения).

Дове­рительный интервал составит

(10)

Таким образом, доверительный интервал для доверительной вероятности 90; 95 и 99,73% м =±1,65*, 2*<, 3*. В выражении (10), при n <30 вместо ве­личины U_p используется коэффициент Стьюдента _cт (таблица 2 приложения).

(11)

Пример: пусть, выполнено измерение давления срабатывания предохра­нительного клапана, с помощью манометра класс точности которого 4 и предел измерений — 25 МПа. По результатам измерений вычислено среднее арифмети­ческое значение давления срабатывания клапана х=17 МПа, при значении среднеквадратического отклонения =± 0,65 МПа.

Требуемую точность измерения можно определить для различных уров­ней доверительной вероятности (Р_д =0,90; 0,95; 0,9973). Получим соответст­венно величину доверительного интервала _0,90 = ±1,65 * 0,65 = ± 1,07 МПа; _0,95 =±2*0,65 = ±1,3 МПа; _0,9973 = ±3 * 0,65 -±1,95 МПа.

Предел основной абсолютной погрешности для манометра можно опре­делить из выражения (2)

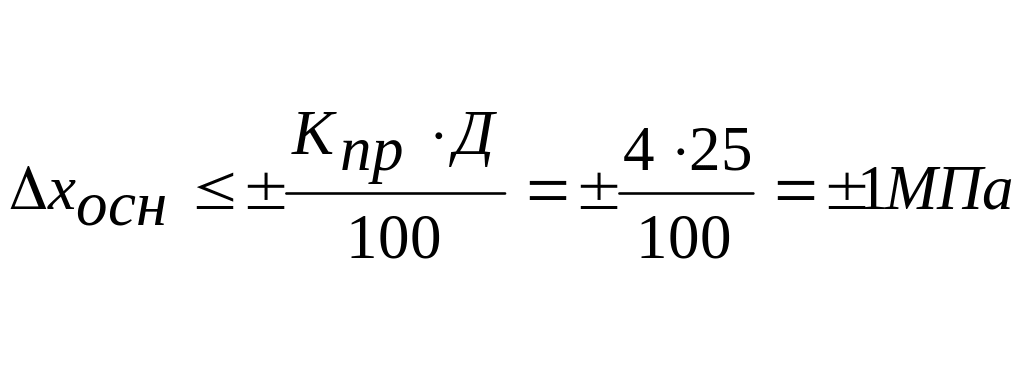
Это означает, что на любой отметке шкалы абсолютная погрешность не должна превышать данного значения. Однако с вероятностью 95% абсолютная погрешность может составлять ±1,3 МПа (по результатам проведенных заме­ров). Столь высокое значение абсолютной погрешности указывает на наличие существенных недостатков в методике измерения или на ее недостаточное ос­воение экспериментатором.

Из приведенного примера можно сделать следующие выводы.

1. При выборе средства измерения с целью уменьшения погрешностей необходимо стремиться к тому, чтобы ожидаемое значение измеряемой физической величины, находились в последней трети диапазона измерений (шкалы прибора).

2. При оценке результатов измерений необходимо учитывать значение среднеквадратичной погрешности, рассчитанной по данным, полученным в реальных условиях применения средств измерения.