Международный университет природы, общества и человека «Дубна»

Кафедра высшей и прикладной математики

Кафедра социологии и гуманитарных наук

Курсовая работа

по Теория вероятностей и математическая статистика

Исследование статистической зависимости двух случайных величин

Выполнил: студент группы 2132

Петык Роман Анатольевич

Руководитель: Г.Э. Гришанина

Дубна, 2012

Оглавление

Введение 3

Основные понятия 3

Задачи 4

Исходные данные 4

Диаграмма рассеяния 10

Корреляционная таблица 12

Вычисление выборочных параметров по корреляционной таблице 13

Гистограмма 14

Полигон 15

Эмпирическая функция распределения 16

Диаграмма рассеивания с линейной регрессией 17

Вычисление параметров линейной регрессии 18

Диаграмма рассеивания с параболической регрессией 19

Вычисление параметров уравнения параболической регрессии 20

Введение

Основные понятия

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.¹

Математическая статистика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала (например, оценить необходимый объем выборки для получения результатов требуемой точности при выборочном обследовании).²

Генеральная совокупность — совокупность всех объектов (единиц), относительно которых ученый намерен делать выводы при изучении конкретной проблемы. Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность — это все население определенного региона (например, когда изучается отношение потенциальных избирателей к кандидату); чаще всего задается несколько критериев, определяющих объект исследования. Например, женщины 10-89 лет, использующие крем для рук определенных марок не реже раза в неделю и имеющие доход не ниже $150 на одного члена семьи.³

Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определенной процедуры выбранных из генеральной совокупности для участия в исследовании.

Характеристики выборки:

• Качественная характеристика выборки — кого именно мы выбираем и какие способы построения выборки для этого используем.

• Количественная характеристика выборки — сколько случаев выбираем, другими словами объем выборки.

Необходимость выборки:

• Объект исследования очень обширный. Например, потребители продукции глобальной компании — огромное количество территориально разбросанных рынков.

• Существует необходимость в сборе первичной информации.¹

Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение , либо коэффициент корреляции 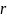. В случае, если изменение одной случайной величины не ведет к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.²

Остальные понятия и определения (в особенности те, что имеют формулы) будут даны по ходу работы.

Задачи

1. Построить диаграмму рассеивания.

2. Вычислить выборочные параметры: выборочные средние, выборочные и исправленные дисперсии, средние квадратические отклонения, моды и медианы выборки по X и по Y.

3. Вычислить корреляционный момент и коэффициент корреляции.

4. Построить корреляционную таблицу (8 на 8).

5. Построить полигоны, гистограммы нормированных относительных частот, эмпирические функции распределения по X и по Y.

6. Вычислить выборочные параметры: выборочные средние, выборочные и исправленные дисперсии, средние квадратические отклонения, моды и медианы выборки по X и по Y по корреляционной таблице.

7. Вычислить параметры для уравнения линейной регрессии Y на X, построить линию регрессии на диаграмме рассеивания.

8. Вычислить параметры для уравнения параболической регрессии, построить линию параболической регрессии на диаграмме рассеивания.