9. Теорема Лагранжа и теорема Кастильяно.

Продифференцируем потенциальную энергию, представленную в форме (13-г) по произвольному обобщенному перемещению q_i , учитывая симметрию матрицы жесткости (12), получим:

Отсюда, с учетом (3-а) следует равенство

, (15)

которое составляет содержание теоремы Лагранжа:

Частная производная от потенциальной энергии упругой системы по обобщенному перемещению равна обобщенной силе, соответствующей этому обобщенному перемещению.

Дифференцируя потенциальную энергию, представленную в форме (13-в) по произвольной обобщенной силе Q_i и учитывая симметрию матрицы податливости (11), аналогичным образом получим:

_,

или , (16)

Это соотношение известно как теорема Кастильяно:

Частная производная от потенциальной энергии линейной упругой системы по обобщенной силе равна обобщенному перемещению, соответствующему этой обобщенной силе.

Замечание. Для упругих, но нелинейных систем теорема Лагранжа справедлива в приведенной здесь формулировке, а теорема Кастильяно должна быть откорректирована.

10. Удельная работа напряжений.

Рассмотрим элементарный объем dV выделенный из тела, ограниченный поверхностью А. Выделим элемент поверхности dA, с нормалью , на который действует напряжение S. Работа, которую совершат напряжения, действующие на поверхность А, на приращениях перемещений du определится интегралом:

dW = = (S.u)dA,

где S_x, S_y, S_z, u,v,w – проекции векторов S и du на координатные оси.

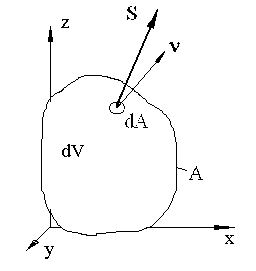
Рис.1. К вычислению работы поверхностных сил.

Выразим проекции вектора S через напряжения по формулам (1.6) и преобразуем интеграл по поверхности в интеграл по объему. Тогда, учитывая уравнения равновесия (1.30), получим:

dW = (_xd_x + _yd_y + ... + _zxd_zx ) dv = ( d) dv,

а работа, совершаемая напряжениями, отнесенная к единице объема материала,

= _xd_x + _yd_y + ... + _zxd_zx = ( d), (17)

где ( d ) – двойное скалярное произведение или свертка тензора напряжений и тензора приращений деформаций.

Будем рассматривать компоненты тензора деформаций как обобщенные перемещения, характеризующие деформирование единичного объема материала. Тогда, в соответствии с (17) и определением, данным в п.1, компоненты тензора напряжений оказываются соответствующими им обобщенными силами.

11. Потенциальная энергия упругого тела.

В упругих телах работа (17) накапливается в виде потенциальной энергии:

dп = = _xd_x + _yd_y + ... + _zxd_zx = ( d), (18)

где п - потенциальная энергия единицы объема.

Приращение потенциальной энергии единицы объема, вызванное работой напряжений равно свертке тензора напряжений с тензором приращений деформаций.

12. Соотношения между напряжениями и деформациями и потенциальная энергия линейного упругого тела.

У линейного упругого тела компоненты тензоров напряжений и деформаций связаны линейными зависимостями.

() = (а)(), (19)

или () = (с)(), (20)

где ()=(_x,_y,_z,_xy,_yz,_zx)^T - матрица-столбец, составленная из компонент тензора деформаций,

() = (_x,_y,_z,_xy,_yz,_zx)^Т - матрица-столбец, составленная из компонент тензора напряжений,

(а) – матрица (6х6) упругих коэффициентов податливости материала,

(с) = (а)^-1 _{_}-_{_} матрица упругих коэффициентов жесткости материала.

В п.10 показано, что компоненты тензоров деформаций и напряжений могут быть интерпретированы как обобщенные перемещения и соответствующие им обобщенные силы. Поэтому матрицам (а) и (с) присущи все свойства, описанные в п.п. 7 и 8 для матриц жесткости и податливости линейных упругих систем.

Следовательно, обе матрицы симметричны относительно главной диагонали. Поэтому из 36 коэффициентов каждой из них 21 коэффициент может быть независимым. В общем случае линейно упругого материала его упругие свойства описываются 21-й упругой постоянной.

Потенциальная энергия единицы объема линейного упругого тела п может быть представлена в виде однородной квадратичной функции компонент тензора напряжений, коэффициентами которой являются компоненты матрицы податливости:

п () = (21)

или однородной квадратичной функцией компонент тензора деформаций, коэффициентами которой являются компоненты матрицы жесткости:

п () = (22)

И, наконец, формула (13) в обозначениях этого параграфа принимает вид:

п (,) = 1/2(_x_x + _y_y + ... + _zx_zx) =1/2 ( ), (23)

следовательно,

потенциальная энергия единицы объема линейного упругого тела равна половине свертки тензора напряжений с тензором деформаций.

Если известны функции (21) или (22), то уравнения, связывающие напряжения и деформации могут быть получены по формулам теорем Лагранжа (15) и Кастильяно (16):

_j = (24)

_j = (25)

Разумеется, что те же результаты получатся, если коэффициенты квадратичных форм (21) и (22) подставить в соотношения (19) и (20).

Преобразуем выражение (23), представив тензоры напряжений и деформаций суммой шаровых тензоров и девиаторов:

 = ₀ I + D_ , ₀ = ,

 = 1/3  I + D_ ,  = _x+_y+_z

где I – единичный тензор, ₀ –среднее нормальное напряжение,  - относительное изменение объема. Получим

п = 1/2(₀ I + D_) (1/3  I + D_) =

=1/6 ₀ (I  I) +1/2₀(I  D_) +1/6(D_  I) +1/2 (D_  D_ ) (26).

Вспомним, что девиатор – это такой тензор, у которого равен нулю первый инвариант, то есть сумма элементов, стоящих на главной диагонали. Легко проверяется, что свертка девиатора с единичным тензором равна нулю, поэтому в ноль обращаются второе и третье слагаемые в (26). Свертка двух единичных тензоров равна 3, поэтому первое слагаемое превращается в 1/2₀.

В результате, формула (26) принимает вид:

п = 1/2₀ + 1/2 (D_  D_ ) = п_ио + п_иф. (27)

Первое слагаемое называют энергией изменения объема:

п_ио = 1/2₀ (28),

а второе – энергией изменения формы:

п_иф = 1/2 (D_  D_ ) (29).