4.3. Закон Гука при произвольном напряженном состоянии в произвольных координатны осях.

Пусть произвольные оси x, y, z наклонены к главным осям 1, 2, 3 под углами, косинусы которых образуют матрицу (L):

(L) = 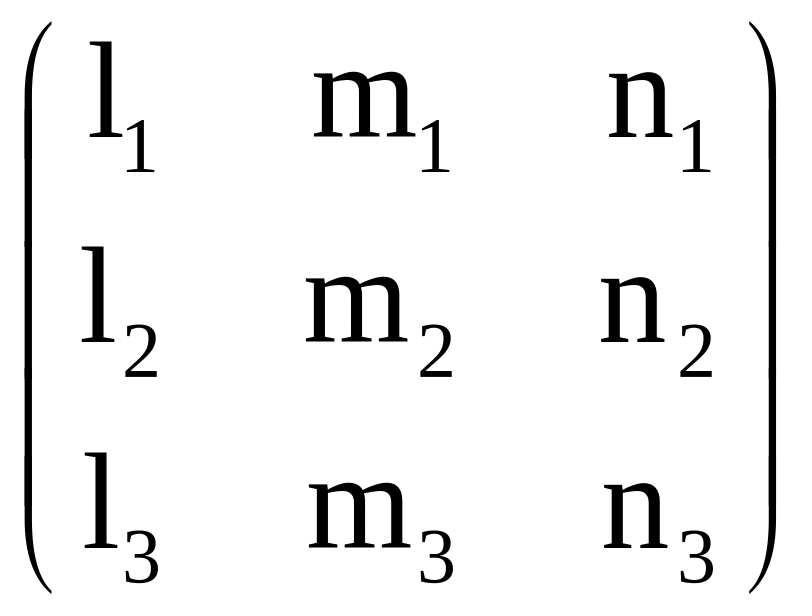(6)

При повороте осей компоненты напряжений преобразуются по формулам (1.9) Поскольку исходные оси 1, 2, 3 главные, формулы (9.1-а) принимают вид:

_x =

_y = (7)

_z = ,

_xy =

_yz = ............

_zх = ............

Компоненты тензора деформаций преобразуются по аналогичному закону:

_x =

_y = (8)

_z = ,

1/2_xy =

1/2_yz = ............

1/2_zх = ............

Задача состоит в том, чтобы выразить компоненты деформаций _x, _y, _z, _xy, _yz, _zx через напряжения _x, _y, _z, _xy, _yz, _zx.

Для ее решения в первую формулу из (8) подставим значения главных деформаций из (5):

_x = =

К множителю при  в фигурной скобке добавим ₁l²  ₂m²  ₃n². Получим:

_x =

Учитывая, что

₁ + ₂ + ₃ = _x + _y + _z , (это первый инвариант тензора напряжений),

l₁² + m₁² + n₁² = 1,

= _x (первая формула из (7)),

получим:

_x = ,

Аналогично получаются формулы для двух других линейных деформаций _y и _z.

Следовательно, в произвольных осях линейные деформации _x, _y и _z связаны с нормальными напряжениями _x, _y и _z такими же зависимостями, какими главные деформации связаны с главными напряжениями (5).

Теперь определим деформацию сдвига из четвертой формулы (8):

_xy =2 ( ) =

- }]

(К выражению в фигурной скобке добавлено  ₁l₁l₂  ₂m₁m₂  ₃n₁n₂ ).

Учитывая, что из (8) следует = _xy , а из условия ортогональности новых осей , получим:

_xy , (9)

где G = (10)

Упругая постоянная материала G называется модулем сдвига или модулем упругости при сдвиге. Модуль сдвига связывает деформацию сдвига  с касательным напряжением  ,которое ее вызывает.

Аналогично получаются выражения для деформаций _yz и_zx. Полностью система уравнений закона Гука для изотропного тела в произвольных осях имеет вид:

_x = _xy =

_y = _yz = (11)

_z = _zx =

4. Относительное изменение объема.

Относительное изменение объема в соответствии с (2.21) определяется через компоненты деформаций:

 = _x + _y + _z. (12)

Выразим его через компоненты напряжений, используя соотношения (11):

или  = (13)

где _ср = - среднее нормальное напряжение,

К - модуль объемной упругости (объемный модуль упругости) – упругая характеристика, связывающая относительное изменение объема со средним нормальным напряжением:

K = . (14)

5. Обратные соотношения. Закон Гука в форме Ламе.

Обратим соотношения (11), выразим напряжения через деформации. Из первого уравнения (11) получим:

_x = E_x + (_y+ _z)

_x +_x = E_x +(_x + _y + _z) ,

Отсюда, учитывая (13), получим

_x =

Это уравнение, принято записывать в виде:

_x =  + 2G_x,

где G – модуль сдвига (10),  - упругая постоянная Ламе:

 = (15)

Два другие нормальные напряжения выражаются аналогично, обращение трех оставшихся уравнений (11) комментариев не требует. Получется следующая система уравнений закона Гука, выражающих компоненты напряжений через деформации:

_x =  + 2G_x, _xy = G _xy

_y =  + 2G_y, _yz = G _yz (16)

_z =   + 2G_z, _zx = G _zx

Их называют уравнениями закона Гука в форме Ламе.

Первые три равнения можно преобразовать (проверьте сами)и тогда уравнения (16) примут вид:

_x = ^*(_x + (_y + _z)) _xy = G _xy

_y = ^* (_y + (_x + _y)) _xy = G _xy (17)

_z = ^* (_z + (_y + _x)) , _xy = G _xy

где  = , . (18)

По форме эти обратные соотношения тождественны прямым уравнениям закона Гука (11).