3. Физические уравнения.

3.1. Общие соотношения.

3.2. Удельная работа напряжений.

3.3. Потенциальная энергия.

4. Закон Гука для изотропного упругого тела.

4.1. Линейное напряженное состояние.

4.2. Закон Гука для произвольного напряженного состояния в главных осях тензора напряжений.

4.3. Закон Гука при произвольном напряженном состоянии в произвольных координатны осях.

4.4. Относительное изменение объема.

4.5. Обратные соотношения. Закон Гука в форме Ламе.

4.6. Соотношение между девиаторами и интенсивностями напряжений и деформаций.

4.7. Характеристики упругих свойств материалов.

4.8. Потенциальная энергия изотропного материала.

4.9. Заключение по главе. Линейно- упругая модель и реальные материалы.

4.10. Пример.

3. Физические уравнения.

3.1. Общие соотношения.

Физические уравнения в механике сплошных сред связывают параметры, описывающие напряженное состояние с переменными, описывающими движение или деформирование материала. В теории упругости физические соотношения связывают тензор напряжений  с тензором деформаций . В линейной теории упругости, которая здесь излагается, предполагается, что эта связь линейна.

В общем случае линейная зависимость между тензорами напряжений  и деформаций  имеет вид линейных уравнений, связывающих компоненты этих тензоров:

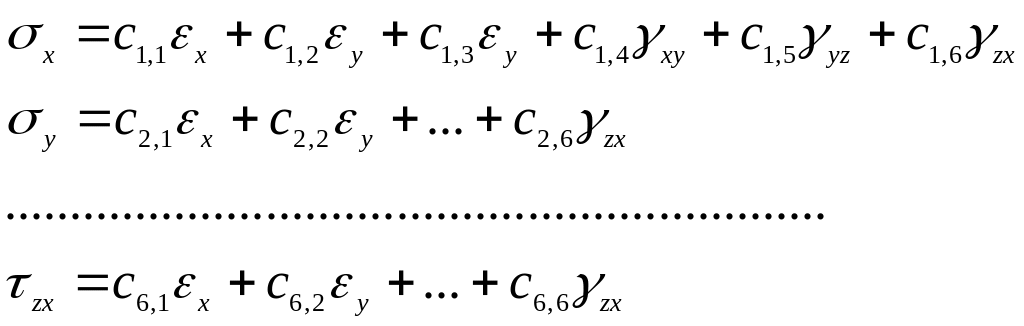
(1)

или, то же самое:

() = [С]() , (1-м)

где () = (_x,_y,_z,_xy,_yz,_zx)^T – матрица-столбец, составленная из компонент тензора напряжений (шестимерная по числу независимых компонент),

() = (_x,_y,_z,_xy,_yz,_zx)^T – матрица-столбец, составленная из компонент деформаций.

[C] – матрица (6х6) упругих коэффициентов жесткости.

Обратив уравнения (1), получим линейные соотношения, выражающие деформации через напряжения:

() = [А] () , (2)

где [А] – матрица упругих коэффициентов податливости, обратная матрице [С]:

[А] = [С]^-1, [С] = [А]^-1.

3.2. Удельная работа напряжений.

В механике принято работу, которую совершают внешние силы над механической системой считать положительной (в классической термодинамике обычно принимается обратное правило знаков).

Рассмотрим элементарный объем V выделенный из тела в нагруженном состоянии, ограниченный поверхностью А. (объем обозначен V, а не dV, поскольку по нему предстоит интегрировать). Выделим элемент поверхности dA, с нормалью , на который действует напряжение S (рис.1).

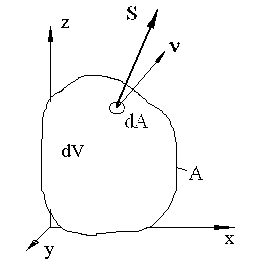
Рис.1. Элементарный объем.

Работа, которую совершат напряжения S на приращениях перемещений du определится интегралом:

dW = = (Sdu)dA,

где S_x, S_y, S_z, du_x, du_y, du_z – проекции векторов S и du на координатные оси.

Выразим проекции вектора S через напряжения по формулам (1.6) и преобразуем интеграл по поверхности в интеграл по объему. Тогда, учитывая уравнения равновесия (1.30), получим:

dW= (_xd_x + _yd_y + ... + _zxd_zx ) dv

Поскольку объем V бесконечно малый,

dW = (_xd_x + _yd_y + ... + _zxd_zx ) = V (_xd_x + _yd_y + ... + _zxd_zx )

Работа, приходящаяся на единицу объема:

dw = = _xd_x + _yd_y + ... + _zxd_zx = d (3)

Если компоненты деформаций _ij принять за обобщенные перемещения, то компоненты напряжений _ij c теми же индексами можно рассматривать как соответствующие им обобщенные силы, поскольку они совершают работу на приращениях d_ij.

Тензорная операция, обозначенная в зависимости (26) двумя точками, называется сверткой или двойным скалярным произведением тензоров. По определению ее результатом является скаляр, равный сумме произведений одноименных компонентов перемножаемых тензоров. Прямая проверка позволяет убедится в том, что свертка тензоров A и B равна первому инварианту (т.е. сумме элементов, стоящих на главной диагонали,) скалярного произведения этих тензоров:

:AB = = J1(AB) = J1((A)^Т.(B)) (4)

3.3. Потенциальная энергия.

В упругих механических системах работа, совершаемая внешними силами, накапливается в виде потенциальной энергии. Приращение потенциальной энергии единицы объема dП равно работе, совершаемой напряжениями (3):

dП = dw = _xd_x + _yd_y + ... + _zxd_zx (5)

или

dП = d . (6)

Приращение потенциальной энергии единицы объема, вызванное работой напряжений равно свертке тензора напряжений с тензором приращений деформаций.

Представим тензоры, входящие в (6) суммами их шаровых частей и девиаторов.

 = (₀ I  D_ ) , d = (  I + D_d) .

Учитывая, что свертка тензоров следует правилам обычного умножения, получим:

dП(₀ I  D_)  ( I + D_d) =

= ₀ (I  I) + ₀ (I  D_d) + (D_  I) + (D_  D_d) (7)

Легко проверяется, что свертка двух единичных тензоров (в первом слагаемом (7)) равна 3, а свертки единичных тензоров с девиаторами (во втором и третьем слагаемых) равны нулю. Поэтому в (7) остается только два слагаемых – первое и последнее:

dП = ₀d + D_  D_d (8)

Потенциальная энергия является функцией обобщенных сил или функцией однозначно связанных с ними обобщенных перемещений. Следовательно, потенциальная энергия может быть представлена в виде функции компонент напряжений или в виде функции компонент деформаций

П = П(_ij) или П = П(_ij). (9)

Воспользовавшись вторым из этих представлений запишем полный дифференциал потенциальной энергии в виде:

dП = . (10)

Сравнивая (10) с (5), получим:

_i,j = . (11)

Компоненты напряжений являются производными от потенциальной энергии по соответствующим компонентам деформаций.

Этот результат является прямым следствием теоремы Лагранжа - производная от потенциальной энергии по обобщенному перемещению равна той обобщенной силе, которая соответствует этому обобщенному перемещению. Заметим, что, как и теорема Лагранжа, зависимость (9) справедлива как для линейных, так и для нелинейных упругих систем.

В линейных упругих системах компоненты напряжений и деформаций связаны линейными зависимостями (1). Нетрудно показать, а еще проще проверить, что в этом случае потенциальная энергия упругой системы является однородной квадратичной функцией компонент деформаций:

П = , i,j = 1,2…6, (12)

коэффициентами которой являются компоненты матрицы упругих коэффициентов жесткости [А] (см. (1)).

Можно представить потенциальную энергию упругого тела в виде функции компонент напряжений:

П = , i,j = 1,2…6. (13)

В этом выражении коэффициентами квадратичной формы являются компоненты матрицы упругих коэффициентов жесткости [С], которая обратна матрице коэффициентов податливости (см.(3)).

Используя уравнения (1) или (2), выражения (12) или(13) можно привести к виду:

П = = (), (14)

Потенциальная энергия единицы объема линейного упругого тела равна половине свертки тензоров напряжений и деформаций.

Как известно, вторая смешанная производная функции нескольких переменных не зависит от порядка дифференцирования. Дифференцируя выражение (10) сначала по _i и _j, а затем меняя порядок дифференцирования, получим:

А_i,j = A_j,i (13)

Коэффициенты матрицы [А] не меняются при перестановке индексов, матрица симметрична относительно главной диагонали. Аналогично устанавливается симметрия матрицы коэффициентов жесткости [С].

Матрицы упругих коэффициентов жесткости и податливости симметричны относительно главной диагонали.

Следовательно, из 36 коэффициентов у каждой из матриц А и С независимыми являются 21 коэффициент.