1.7. Наибольшие касательные напряжения и площадки, на которых они действуют.

Пусть известны главные напряжения (₁ ₂ ₃) и главные площадки. Касательные напряжения на этих площадках равны нулю, а на прочих, неглавных площадках они от нуля отличны. Найдем среди этих площадок такие, на которых касательные напряжения максимальны.

Для этого найдем касательные напряжения на произвольной площадке, направляющие косинусы нормали  к которой обозначим l,m и n. Квадрат полного напряжения на этой площадке определим как сумму квадратов его проекций на главные оси:

(S_)² = S_x²+S_y²+S_z²

Применяя к главным осям формулы (6), получим:

(S_)² = ,

Для определения квадрата нормального напряжения можно воспользоваться первой из формул (9-а):

_² = ( )² (14)

Тогда квадрат касательного напряжения определится выражением

² =(S_)² - _² = - ( )², (15-а)

или в форме, более удобной для последующих преобразований:

² = - _². (15-б)

У функции ² нужно искать экстремум. Задача осложняется тем, что аргументы этой функции – направляющие косинусы l,m и n – взаимозависимы, они связаны условием (11). Для отыскания условного экстремума воспользуемся методом неопределенных множителей Лагранжа [ ], в соответствии с которым экстремум ищется для функции

(l,m,n)= ² + (l²+m²+n²-1),

, где – множитель Лагранжа. Или, с учетом (15-б),

(l,m,n)= - _² + (l²+m²+n²-1), (16)

При выполнении условия (11) экстремумы  совпадают с экстремумами функции ², но направляющие косинусы в выражении (16) можно рассматривать как независимые.

Дифференцируя  по l,m и n с учетом (14) и приравняв нулю производные, получим три уравнения, выражающие условия экстремальности  или:

2(₁² – 2_₁ + )l =0 (1)

2(₂² – 2_₂ + )m =0 (2) (17)

2(₃² – 2_₃ + )n =0 (3)

Вместе с (11) они составляют систему 4-х уравнений с четырьмя неизвестными l,m,n и .

Исследуя решения системы уравнений (17)+(11) рассмотрим 4 следующих варианта:

Вариант 1. Все три направляющих косинуса равные нулю всегда удовлетворяет системе (17), но не удовлетворяет уравнению (11), следовательно, решением не является.

Вариант 2. Два направляющих косинуса равны нулю, а третий в соответствии с уравнением (11) равен единице.

Пусть, например, n=1, а l= m =0. В этом случае из (14) получается _ = ₃ , первое и второе уравнения из (17) удовлетворяются тождественно, а третье принимает вид ₃² –_₃+=0. оно выполняется при  = ₃. Из (15) получаем ² = 0. Таким наборам направляющих косинусов соответствуют исходные главные площадки, на них касательные напряжения равны нулю, это экстремумы функции ², но не максимумы, а минимумы.

Вариант 3. Один направляющий косинус равен а два не равны нулю.

Пусть, например, l=0 , m≠0, n≠0. Из (14) получим

_ = . (а)

Первое уравнение из(17) удовлетворяется тождественно, а второе и третье приводятся к системе уравнений

₂² – 2_₂ +  = 0 (б)

₃² – 2_₃ +  = 0 (в).

Вычитая (в) из (б), получим

₂² - ₃² - 2_(₂-₃) = 0, откуда

_ = .

Сравнивая последнее выражение с (а), получаем m² = n² = , т.е m = ± , n = ± . Это решение удовлетворяет уравнению (11) и определяет площадки, на которых касательные напряжения максимальны. Значение касательного напряжения на этих площадках найдем, подставив полученные направляющие косинусы в (15):

² = - = или =

Найденная площадка перпендикулярна к главной площадке с напряжение ₁ и наклонена под углом /4 к главным площадкам с напряжениями ₂ и ₃ .

Аналогино можно найти еще два семейства площадок с максимальными касательными напряжениями. Все результаты сведены в таблицу.

	l	m	n	
1	0	±	±	1=
2	±	0	±	2=
3	±	±	0	3=

Если главные напряжения пронумерованы в соответствии с традиционным правилом ₁  ₂  ₃, то абсолютному максимуму соответствует напряжение ₂.

_мах = ₂ = (18).

Ориентация площадок, на которых они действуют показана на рис.1.7.

Вариант 4. Все три направляющих косинуса отличны от нуля. Решений нет.

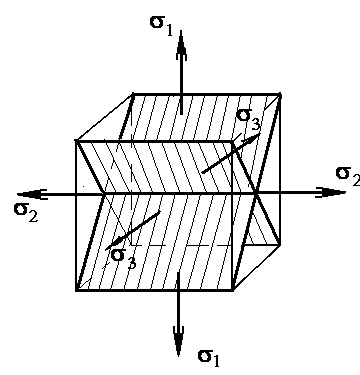
Рис.1.7. Площадки, на которых действуют

максимальные касательные напряжения.