2.6. Тензор малых деформаций.

Представим тензор-градиент перемещений (u) в виде суммы симметричного и антисимметричного тензоров:

(u) = 1/2((u) + (u)^Т ) +1/2((u) -(u)^Т)

В развернутом виде:

(u)

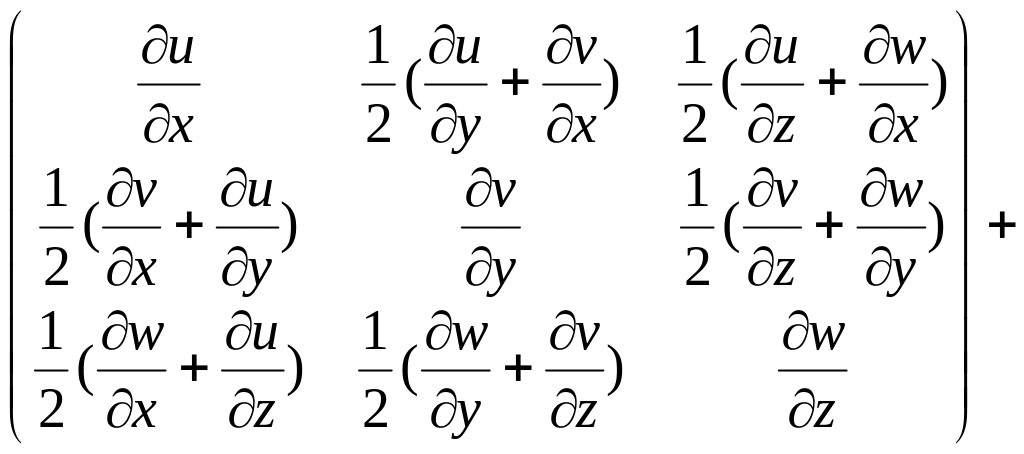
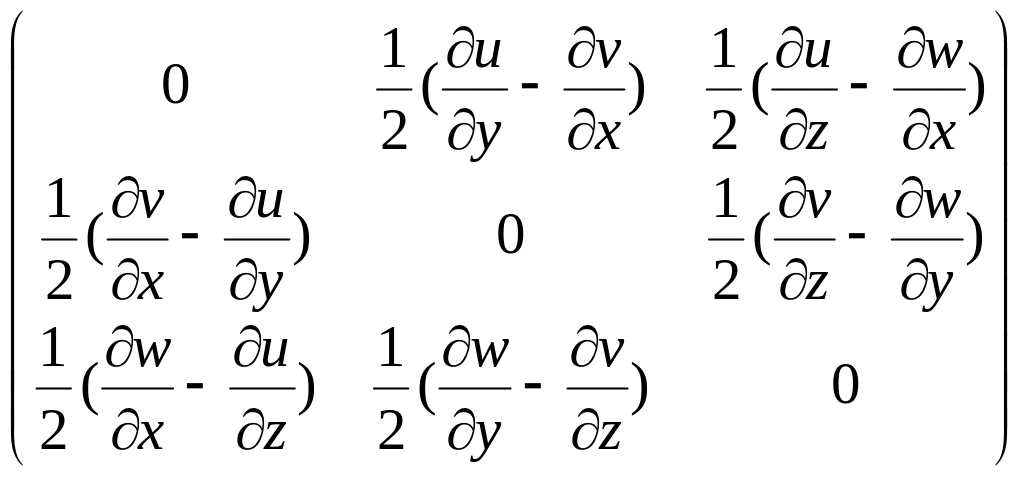(14)

Симметричный тензор содержит компоненты деформаций (см.(8)), от которых зависят удлинения любых бесконечно малых векторов, исходящих из выбранной точки, Следовательно, симметричный тензор описывает деформированное состояние окрестности точки А. Его называют тензором (малых) деформаций:

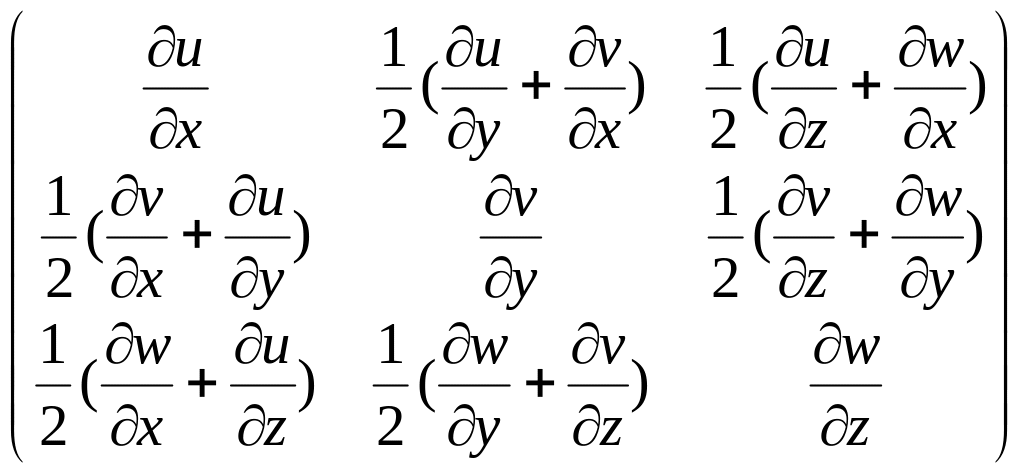
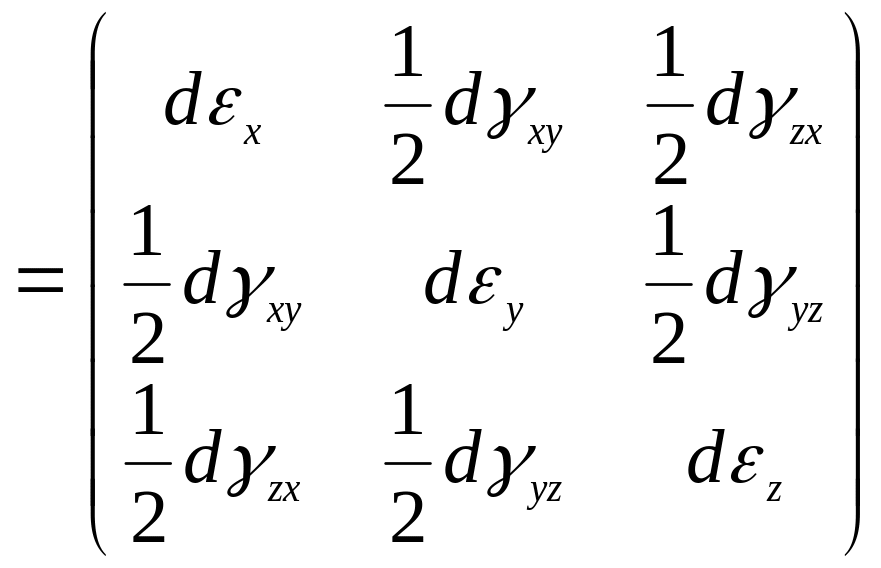()= (15)

Диагональными компонентами этого тензора являются относительные удлинения , а недиагональными – половины деформаций сдвига. Заметим, что , структура, матрица которой не содержит множителя при _ij, не тензор, в частности, ее компоненты при повороте осей координат не преобразуются по формулам преобразования компонент тензора.

Антисимметричный тензор описывает движения, происходящие без деформирования, без изменения расстояний между смежными точками, то есть описывает повороты окрестности точки как твердого тела. Будем называть его тензором вращения:

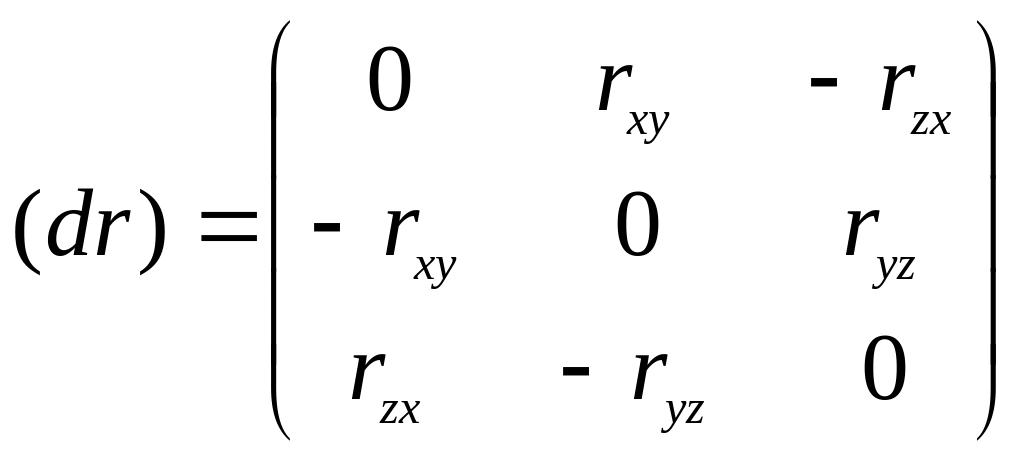(16)

где

(17)

2.7. Свойства тензора деформаций.

Поскольку компоненты деформаций образуют симметричный тензор, такой же как тензор напряжений, все свойства, установленные в главе 2 для тензора напряжений могут быть распространены на тензор деформаций.

Преобразование при повороте осей координат.

Матрица ()содержит компоенты деформаций по направлениям осей принятой системы координат и приращения сдвигов между этими направлениями. Заменим систему координат на новую систему, повернутую относительно старой. То же самое деформированное состояние, то есть тот же самый тензор деформаций (), в новой системе будет представлен другими компонентами – относительными удлинениями и сдвигами в новых направлениях образующими матрицу (¹. Матрица деформаций преобразуется к новым осям (см. приложение ) в соответствии с формулой:

¹ (L) (L)^T (18)

где

(L) – матрица направляющих косинусов новых осей по отношению к старым (приложение ).

Главные оси и главные значения тензора деформаций.

Для любого тензора деформаций  можно можно найти такое положение координатных осей, при котором недиагональные элементы матрицы ( (т.е. деформации сдвига) обратятся в ноль, матрица ( станет диагональной:

(¹ =

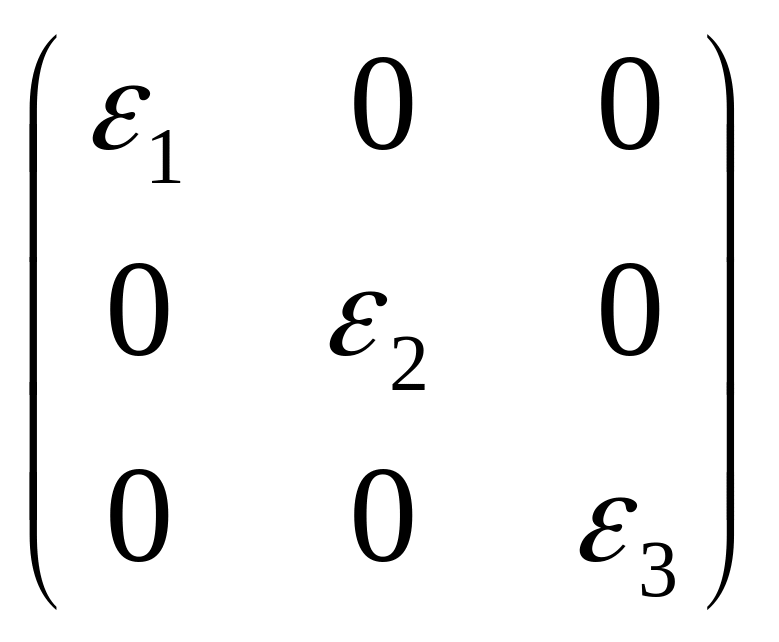
Такие оси называют главными осями тензора деформаций, относительные удлинения по направлениям этих осей называют главными деформациями.

Главные деформации являются корнями кубического характеристического уравнения

³ - J1_*² + J2_* - J3_ = 0, (19)

где J1_, J2_, J3_ - главные инварианты тензора деформаций, которые в технических обозначених выражаются формулами:

J1_ = _x + _y + _z,

J2_ = _x_y + _y_z + _z_x - _xy² - _yz² - _zx² (20)

J3_ = _x_y_z + 2_xy_yz_zx – _yz_x ²– _zx_y² – _xy_z²

Необходимость в определении направлений главных осей по компонентам тензора () появляетсяредко.

Все формулы, выведенные в гл.2 для компонент напряжений можно просто переписать для компонент тензора деформаций, для этого необходимо в них заменить нормальные напряжения (_x, _y, _z, ₁, ₂, ₃) на соответствующие линейные деформации (_x , _у, _z, ₁, ₂, ₃), а касательные напряжения (_xy, _yz, _zx) на половины соответствующих сдвигов (то есть на 1/2_xy, 1/2_yz, 1/2_zx).

Например, по аналогии с разделом 1.7 и формулой 1.18, наибольшие сдвиги происходят между направлениями, перпендикулярными к главному направлению ₂ и наклоненными под углом 45^о к осям ₁ и ₃. Величина максимального сдвиг составляет

_мах = ₁ - ₃