2. Теория деформаций

2.1. Деформации.

2.2. Перемещения. Градиент перемещений.

2.3. Линейная теория деформаций.

2.4. Относительные удлинения произвольного вектора. Компоненты деформаций. Уравнения Коши.

2.5. Геометрический смысл компонентов деформаций.

2.6. Тензор малых деформаций.

2.7. Свойства тензора деформаций.

2.8. Относительное изменение объема.Девиатор деформаций.

2.9. Интегрирование уравнений Коши.

2.10. Уравнения совместности деформаций.

2. Теория деформаций.

2.1. Деформации.

Деформированием тела называют такие его движения, при которых меняются расстояния между его материальными точками, то есть меняются его размеры и/или форма.

Деформациями будем называть любые величины, характеризующие деформированное состояние тела.

Деформации в твердом теле могут вызываться разными причинами: нагрузками, изменением температуры, воздействием электрических или магнитных полей, радиационным облучением, изменением влажности (в органических материалах) и т.д.. В этом разделе мы обсудим общие свойства деформаций, не зависящие от причин, которые их вызвали.

2.2. Перемещения. Градиент перемещений.

Движение деформируемого тела будем описывать в неподвижной ортогональной системе координат xyz (рис.1). Положение материальной точки в исходном (недеформированном) состоянии тела будем задавать радиус-вектором x, его компоненты (координаты точки) будем обозначать x,y,z и при необходимости компоновать в матрицу-столбец (x) = (x,y,z)^Т. Перемещения материальных точек в процессе деформирования будем описывать вектором перемещений u(x), проекции которого на координатные оси u,v,w образуют матрицу-столбец (u)= (u,v,w)^Т.

Выделим в теле до деформации бесконечно малый материальный вектор AB  dx (рис.1), начало которого находится в материальной точке A, с координатой x, а конец в точке B с координатой x+dx (или x+dx, y+dy, z+dz). Длина отрезка АВ равна dx, его проекции на оси координат - (dx,dy,dz). а направляющие косинусы l, m, n:

. (1)

В деформированном состоянии точка А, переместившись на величину u(x), займет положение А₁. Точка В с координатами x+dx переместится на u(x+dx) или, (что то же самое), на u(x)+du и займет положение В₁. Вектор AB в результате деформации превратился в вектор A₁B₁, длина которого dx₁.

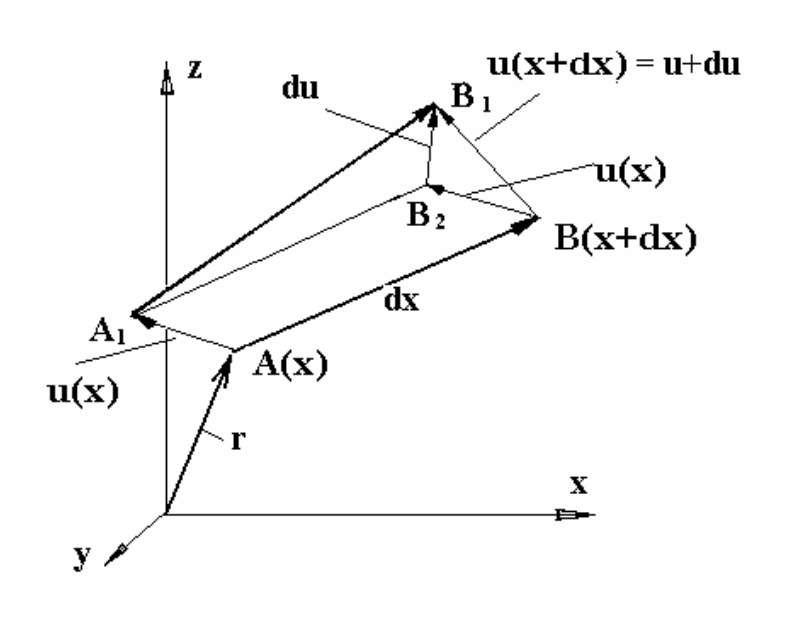
Рис.1. Координаты и перемещения.

Отложим от точки В вектор перемещения точки А, то есть вектор u(x) = ВВ₂. Как видно из рисунка, векторная разность перемещений точек А и В представляется вектором В₂В₁:

В₂В₁ = u(x+dx) - u(x) = du, (2)

С другой стороны, из того же рисунка видно, что вектор du представляет собой разность векторов A₁B₁ и A₁B₂= AB, то есть

du = dx₁ - dx или dx₁ = dx + du. (3)

Вектор du может быть представлен в виде:

du=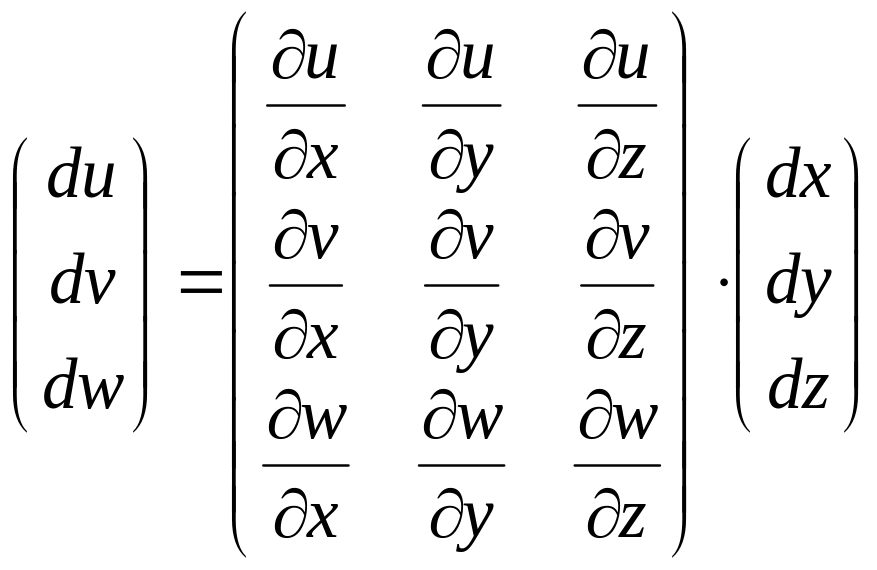 = (u)  (dx) (4)

Матрица (u), составленная из частных производных от проекций вектора перемещений по координатам, связывает линейно два вектора du и dx. и, следовательно в соответствии с 1.???, (см. ) определяет тензор второго ранга u , который называют градиентом перемещений. Как будет показано в дальнейшем, этот тензор характеризует деформирование и вращение окрестности материальной точки А.

2.3. Линейная теория деформаций.

Ограничения. Введем два ограничения:

О1. Деформации малы - изменение длины любого вектора много меньше его первоначальной длины, относительное удлинение вектора много меньше единицы:

dx₁ - dx << dx , (О1)

О2. Малы повороты любых материальных элементов, в частности любых материальных векторов:

<<1 , tg  Sin  , (О2)

где  - угол поворота материального элементарного отрезка. (см. рис. 2).