Балтийский Государственный Технический Университет

Факультет авиа- и ракетостроения

Гидрогазоаэродинамика

Курсовая работа

Обтекание треугольновидного профиля сверхзвуковым потоком

Выполнил: Проверил: Зазимко В.А.

Санкт-Петербург

2012

Оглавление

1.Понятие о методе характеристик 3

2. Характеристические уравнения для установившегося плоского безвихревого сверхзвукового течения газа. 4

3.Уравнение неразрывности в плоской естественной системе координат для установившегося движения. 5

4.Приведение уравнений газодинамики для плоского установившегося безвихревого течения идеального газа к характеристическому виду. 5

5.Определение функции Прандля-Майера 7

6.Течение Прандля-Майера 9

7. Некоторые понятия об ударных волнах. 10

8.Прямой скачок уплотнения 12

8.1.Связь между скоростями 13

8.2.Связь между плотностями 13

8.3.Связь между давлениями 13

8.4.Связь между температурами 13

8.5.Ударная адиабата 14

8.6.Связь между числами Маха 14

8.7.Изменение энтропии на прямом скачке 14

8.8.Потери полного давления на прямом скачке 14

8.9.Формула Релея 14

9.Косой скачок уплотнения 15

10.Приближенное нахождение Cy и Cx 16

11.Нахождение параметров при обтекании сверхзвукового потока углов профиля 17

Расчётная часть 18

Библиографический список: 29

1.Понятие о методе характеристик

Рассмотрим систему двух дифференциальных уравнений в частных производных с двумя независимыми переменными:

(1)

где i=1,2. Сиcтема уравнений называется линейной, если все коэффициенты A_i, B_i, C_i, D_i, E_i или постоянны (система с постоянными коэффициентами) или являются функциями только независимых переменных х, у. Если какие-либо коэф­фициенты, зависят также от искомых переменных и и υ, то система называется квазилинейной. Особо подчеркнем то, что в рассматриваемых системах (линейных или квазилинейных) в каждом слагаемом присутствует не более чем один множитель, представляющий собой производную от искомых величин и или υ. Система называется однорядной, если оба коэффициента E_i= 0.

Многие важные задачи аэрогазодинамики в математическом плане сводятся к решению квазилинейной системы двух уравнений в частных производных с двумя независимыми переменными.

Суть метода характеристик основана на том, что в плос­кости потока имеются особые линии, называемые характе­ристическими кривыми или просто характеристиками. Через каждую точку в потоке проходят две разнонаправленные характеристики, принадлежащие двум разным семействам. Уравнения газодинамики можно преобразовать к такому новому виду, что в каждом отдельном уравнении производные от искомых величин и и υ вычисляются вдоль характеристики одного семейства. Эти направленные производные можно принять за обыкновенные, и тогда газодинамические уравнения превращаются в уравнения в обыкновенных про­изводных. Называются они условиями на характеристиках.

Представим на плоскости независимых переменных х, у некоторую кривую L, определяемую уравнением на которой заданы функции

.

Наш способ решения базируется на получении новых уравнений путем сложения левых частей исходных уравнений системы (1.1), одно из которых домножается на множитель, который затем определяется. Такой способ более прост и доступен.

u=u(x,y) направленная производная

; где

Имеем систему

;

Это эквивалентно двум уравнениям:

- условие на характеристике

- уравнение характеристики

Кривая L сводится к виду

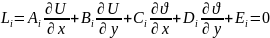, где

Есть 2 варианта решения этого уравнения

1 вариант

, тогда и - условие на характеристике;

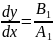и - уравнение характеристики

2 вариант

Оказывается, если система уравнений относится к гиперболическому типу, то всегда можно придти в преобразованных уравнениях к равенству типа (1.5). Для этого достаточно второе уравнение системы (1.1) домножить на некоторый, на первых порах неопреде­лимый, множитель λ и сложить второе уравнение с первым, получая

, тогда , где

и т.д.

следовательно (4₁)

Решая уравнение можно получить:

Если нет вещественных корней, то

Если два кратных корня, то

Если два различных корня, то

Далее рассматривается только гиперболическая система, в итоге два уравнения в частных производных сводятся к двум обыкновенным дифференциальным уравнениям вдоль характеристики.

2. Характеристические уравнения для установившегося плоского безвихревого сверхзвукового течения газа.

(5)

(6)

Так как , , , то (5) и (6) примут вид

(7)

(8)