9. A) Обчислити за теорією Бора радіус r2 другої стаціонарної орбіти і швидкість υ2 електрона на цій орбіті для атома водню.

B) З катодної трубки на діафрагму з вузькою прямокутною щілиною нормально до площини діафрагми падає потік моноенергетичних електронів. Визначити анодну напругу трубки, якщо відомо, що на екрані, який розташований на відстані l = 0,5 м від щілини, ширина центрального дифракційного максимуму x = 10,0 мкм. Ширина щілини b = 0,10 мм.

C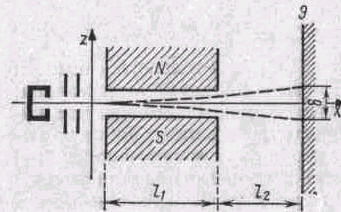 ) Для наближеної оцінки мінімальної енергії електрона в атомі водню можна припустити, що невизначеність Δr радіуса r електронної орбіти і невизначеність Δp імпульсу p електрона на такій орбіті відповідно пов'язані в такий спосіб: Δr  r и Δp  р. Використовуючи ці зв'язки, а також співвідношення невизначеностей, знайти значення радіуса електронної орбіти, що відповідає мінімальній енергії електрона в атомі водню.

D) В досліді Штерна і Герлаха вузький пучок атомів цезію (в основному стані) проходить крізь поперечне неоднорідне магнітне поле и потрапляє на екран (рис.). Яка повинна бути ступінь неоднорідності дВ/дz магнітного поля, щоб відстань b між компонентами розщепленого пучка на екрані була рівна 6 мм? Покласти l₁ = l₂ = 10cм. Швидкість атомів цезію рівна 0,3 км/с.

E) В збудженому атомі гелію один з електронів перебуває в p-стані, другий в d-стані. Знайти можливі зна­чення повного орбітального квантового числа L та відповідного йому моменту імпульсу _L. (в одиницях ħ). Побудувати відповідні векторні діаграми.

10. A) Обчислити за теорією Бора період Т обертання електрона в атомі водню, що перебуває у збудженому стані з головним квантовим числом n = 2.

B) Кінетична енергія протона T = 1 кеВ. Визначити додаткову енергію ΔT, яку необхідно йому надати для того, щоб довжина хвилі λ де Бройля зменшилася в три рази.

C) Середній час життя атома в збудженому стані становить Δt  10^-8 с. Під час переходу атома в нормальний стан випромінюється фотон, середня довжина хвилі < λ > якого дорівнює 600 нм. Оцінити ширину Δλ спектральної лінії, що випромінюється, якщо не відбувається її розширения за рахунок інших процесів.

D ) Вузький пучок атомів рубідію (в основному стані) про­пускається крізь поперечне неоднорідне магнітне поле протя­жністю l₁ = 10 см (рис.). На екрані, віддаленому на відстані l₂ = 20 см від магніту, спостерігається розщеплення пучка на два. Визначити силу F_z, що діє на атоми рубідію, якщо відстань b між компонентами пучка на екрані становить 4 мм і швидкість v атомів дорівнює 0,5 км/с.

E) Система, що складається з трьох електронів, орбітальні квантові числа l₁, l₂, l₃ яких відповідно рівні 1, 2, 3, знаходиться в S-стані. Визначити кут _{1, 2} між орбітальними моментами імпульсу перших двох електронів.

11. A) Обчислити найбільш ймовірну дебройлівську довжину хвилі λ молекул азоту, що містяться в повітрі кімнатної температури.

B) Альфа-частинка міститься в нескінченно глибокому, одномірному, прямокутному потенційному ящику. Використовуючи співвідношення невизначеностей, оцінити ширину l ящика, якщо відомо, що мінімальна енергія α-частинки E_min = 8 МеВ.

C) Хвильова функція, що описує основний стан електрона в атомі водню має вигляд ψ(r)|= А еxp(-r/а₀) ,де А = (πa₀³)^-1/2; а₀ - перший борівський радіус. Визначити 1) імовірність w₁ того, що електрон знаходиться в області, яка обмежена сферою радіусом а₀; 2) імовірність w₂ того, що електрон знаходиться зовні цієї області; 3) відношення цих імовірностей w₂/w₁.

D ) Вузький пучок атомів срібла про­пускається крізь поперечне неоднорідне магнітне поле протя­жністю l₁ = 4 см (рис.). На екрані, віддаленому на відстані l₂ = 10 см від магніту, спостерігається розщеплення пучка на два. Визначити (в магнетонах Бора) проекції _J магнітного моменту атому на напрямок вектора магнітної індукції, якщо відстань b між компонентами пучка на екрані становить 2 мм і швидкість v атомів дорівнює 0,5 км/с.

E) Система, що складається з двох електронів, знаходиться в стані з L = 2. Визначити можливі значення кута  між орбітальним моментом імпульсу p-електрона та повним орбіталь­ним моментом імпульсу  _L системи.

12. A) Визначити зміну енергії ΔE електрона в атомі водню під час випромінювання атомом фотона з частотою ν = 6,2810¹⁴ Гц.

B) З якою швидкістю рухається електрон, якщо довжина хвилі де Бройля λ електрона дорівнює його комптоновській довжині хвилі λ_C?

C) Електрон з енергією E = 100 еВ падає на потенціальний бар’єр висотою U = 64 В. Визначити ймовірність того, що електрон відіб’ється від бар’єру.

D) Визначити можливі значення кута між спіновим моментом імпульсу електрона та повним моментом, якщо електрон перебуває в d-стані.

E) Визначити максимальну проекцію _{J, z max} магнітного моменту атомів ванадію (що знаходиться в стані ⁴F), якщо відомо, що пучок цих атомів при проходженні крізь сильно не­однорідне магнітне поле за методом Штерна і Герлаха розщеплю­ється на 4 складових.

13. A) У скільки разів зміниться період Т обертання електрона в атомі водню, якщо під час переходу в незбуждений стан атом випромінює фотон з довжиною хвилі λ = 97,5 нм?

B) Паралельний пучок моноенергетичних електронів (T = 10 еВ) падає нормально на діафрагму у вигляді вузької прямокутної щілини, ширина якої a. За припущення, що невизначеність координати електрона, який пройшов через щілину, Δx = a, оцінити відносну невизначеність Δp/p імпульсу частинки в двох випадках: 1) a = 10 нм; 2) а = 0,1 нм.

C) Ширина прямокутного потенціального бар’єра d = 0,2 нм. Різниця енергій U – E = 1 еВ. У скільки разів зміниться ймовірність проходження електрона крізь бар’єр, якщо різниця зросте в n=10 разів.

D) Обчислити механічний _j та магнітний момент  _j електрона в основному стані в атомі водню.

E) Визначити кут  між орбітальними моментами ім­пульсів двох електронів, один з яких перебуває в d-стані, а другий — в f-стані, якщо шуканий кут — максимальний.

14. A) На скільки змінилася кінетична енергія електрона в атомі водню під час випромінювання атомом фотона з довжиною хвилі λ = 435 нм ?

B) Оцінити за допомогою співвідношення невизначеностей найнижчий енергетичний рівень електрона в атомі водню. Лінійні розміри атома l ~ 0,1 нм.

C) Електрон перебуває в нескінченно глибокому, одномірному, прямокутному потенційному ящику шириною l. Визначити середнє значення координати < x > електрона

D) Визначити спіновий магнітний момент _s електрона та проекцію магнітного моменту _{s z} на напрямок зовнішнього поля. Які значення може приймати кут між спіновим магнітним моментом та напрямком зовнішнього поля?

E) Визначити максимальну проекцію _{J, z max} магнітного моменту атомів ванадію марганцю (що знаходиться в стані ⁶S ), якщо відомо, що пучок цих атомів при проходженні крізь сильно неоднорідне магнітне поле за методом Штерна і Герлаха розщеплюється на 6 складових.