5. Напряжения в ветвях ремня

Напряжение от предварительного натяжения

ffn = FJ A. (1.22)

Для плоских резинотканевых ремней принимают s 0=1,8 МПа, для синтети ческих s0=10 МПа, для клиновых нормальных ремней s0=1,45 МПа.

С увеличением s 0 снижается долговечность ремня.

Удельная окружная сила (полезное напряжение)

к = F_t / A . (1.23)

Напряжение от натяжения в ветвях ремня при рабочем ходе:

s 1 = F1 / A = s 0 + 0.5k;

s2 = F2 /A = s0 + 0.5k. (⁽.24)

Центробежная сила вызывает напряжения растяжения в р емне, как в свободном вращающемся кольце

s_V = F_V / A = 10 ^-6 pV² . (1.25)

Здесь множитель 10 ⁶ введен для того, чтобы выразить р в МПа. Напряжение изгиба возникает в ремне при огибании шкивов (рис.6).

По закону Гука, s_u = EZ , где Z = y_max / ^x - относительное удлинение волокон на выпукл.й стороне ремня при изгибе; y _max = 0.5(d + 8) и х = 0.5(d + 8); с ледовательно, s_u = E8 / (d + 8).

Толщина ремня 5 мала по сравнению с диаметром d шкива, поэтому м ожно принять s_u = E8 / d , (126)

здесь Е- модуль упругости материала ремня; для резинотканевых ремней E = 100^350 МПа, плоских синтетических ремней Е = 12001400+МПа; клиновых к^рцотканевых ремней Е = 250 ^ 400 МПа; клиновых кордошнуровых Е=500 ^ 600 МПа.

Формула (1.26) позволяет отметить, что основным фактором, определяющим значение напряжений изгиба, является отношение толщины ремня к диаметру шкива. Чем меньше это отношение, тем меньше напряжение изгиба в ремне.

Суммарное максимальное напряжение в ведущей ветви в месте набегания ремня на малый шкив

^s max = ^s 1 + ^s V + ^s u1 = ^s 0 + °-^5k + ^s V + ^s u ^(L27)

Эпюра распределения напряжений по длине ремня изображена на (рис.7). На ней видно, что в местах набегания и сбегания ремней на шкивы

не происходит резких скачков напряжении, так как ремни постепенно меняют радиусы кривизны, но можно отметить напряжение изгиба s_u1 как

наибольшее. Оно может в несколько раз превышать все другие составляющие суммарного напряжения в ремне и, изменяясь по отнулевому циклу, является главной причиной усталостного разрушения ремня. На практике значения s_u1 ограничивается минимально допуст мым 5 /d₁ = 1/40.

Рис. 7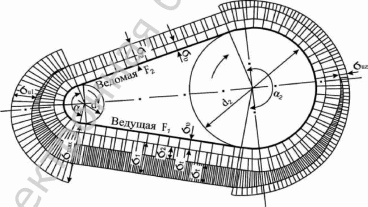

5. Силы, действующие на валы и подшипники

Силы натяжения ветвей ремня нагружают валы и подшипники.

Если ветви ремня параллельны (передаточное отношение близко или равно единице), сила F_e на валы равна двойному начальному натяжению ремня:

F_e = 2F₀ = 2s ₀ A. (1.28)

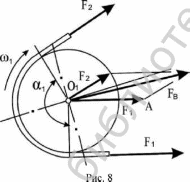
Если ветви ремней не параллельны (передаточное число не равно единице) силу на вал определяют по треугольнику ОАВ (рис.8)

F_e = д/F1² + F^ + 2F1F2 cos(180° - (Х1) » 2F0 sin a1 / 2 (1.29)

Приближение тем справедливее, чем ближе к единице. В передачах без регулирования натяжения его обычно устанавливают с запасом, и оно сохраняется до вытягивания ремня. Поэтому при расчете максимальных сил на валы рекомендуют расчетное начальное натяжение F₀ и напряжение s₀ увеличивать в 1,5 раза.