3. Корреляционный анализ

Одним из основных методов статистического анализа взаимозависимости показателей является корреляционный анализ. При проведении корреляционного анализа предполагают, что данные наблюдений можно считать случайными и выбранными из генеральной совокупности, распределенной по нормальному закону. С помощью корреляционного анализа оценивают не только тесноту связи между показателями, но и решаются задачи отбора факторов, оказывающих наиболее существенное влияние на зависимый признак, обнаружение ранее неизвестных причинных связей. Корреляционный анализ не выявляет причину связей между показателями, но устанавливает количественную меру этих связей и подтверждает достоверность суждений о наличии связи.

При проведении корреляционного анализа вся совокупность данных рассматривается как множество переменных (факторов), каждая из которых содержит n наблюдений.

Основными средствами анализа являются парные коэффициенты корреляции, частные коэффициенты корреляции и множественные коэффициенты корреляции. Коэффициенты не имеют размерности, следовательно, сопоставимы для различных статистических показателей.

Парный коэффициент корреляции характеризует тесноту линейной зависимости между двумя переменными на фоне действия всех остальных показателей, входящих в модель.

При изучении взаимосвязи между двумя переменными их обычно обозначают X и Y. Для двух переменных и коэффициент парной корреляции определяется по формуле:

,

где - оценки дисперсий величин X и Y. Эти оценки характеризуют степень разброса значений вокруг своего среднего значения соответственно, или вариабельность (изменчивость) этих переменных на множестве наблюдений.

Оценки дисперсий определяются по формуле:

, .

Величина парного коэффициента корреляции лежит в пределах от -1 до +1. Если корреляция между случайными величинами положительная, то при возрастании одной случайной величины другая величина имеет тенденцию в среднем возрастать. Если корреляция между случайными величинами отрицательная, то при возрастании одной случайной величины другая величина имеет тенденцию в среднем убывать.

Чем ближе коэффициент корреляции к ±1, чем сильнее зависимость между переменными. Близость абсолютной величины коэффициента корреляции к нулю не означает, что переменные статистически независимы, а лишь указывает на отсутствие линейной связи между ними, что не отрицает возможность существования иной формы зависимости между переменными.

При малых выборках оценка значимости коэффициента корреляции выполняется с использованием t-критерия Стьюдента. Проверяется гипотеза равенства нулю коэффициента корреляции Н₀: ρ=0. При этом фактическое (наблюдаемое) значение t-критерия Стьюдента определяется по формуле:

.

Найденное по этой формуле сравнивается с критическим значением t-критерия, которое выбирается из таблицы значений t-критерия Стьюдента с учетом заданного уровня значимости α и числа степеней свободы (n-2). Если , то полученное значение коэффициента корреляции признается значимым, т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается с вероятностью ошибки α. Таким образом, делается вывод, что между исследуемыми переменными есть тесная статистическая взаимосвязь.

Если совокупность данных состоит из переменной и m независимых переменных (факторов) Х, каждая из которых содержит n наблюдений, то исходные данные для анализа можно записать в матричном виде:

.

На основании данных, содержащихся в этой матрице, вычисляется матрица коэффициентов парной корреляции R:

,

Матрица является симметричной относительно главной диагонали. Анализ матрицы парной корреляции используется при построении моделей множественной регрессии.

Пример 1. В таблице приведены данные, характеризующие деятельность предприятия. Построить матрицу коэффициентов парной корреляции R. Оценить силу связи между объясняемой переменной и объясняющими переменными при уровне значимости α=0,05.

Период t	Прибыль от реализации продукции в % от общего объема прибыли,	Доля продажи в общем объеме продаж в %,	Отпускная цена продукции в руб.,	Коэффициент издержек на единицу продукции,
1 2 3 4 5 6 7 8	10,6 10,9 10,8 11,1 12,7 13 13,2 13,8	20,1 20,6 18,9 23 18,4 17,3 19,6 20,1	1064 1046 1059 1057 1084 1090 1138 1178	32,3 30,2 38,6 28,7 39,5 40,3 47,6 48,4

Продолжение таблицы

Период t	Прибыль от реализации продукции в % от общего объема прибыли,	Доля продажи в общем объеме продаж в %,	Отпускная цена продукции в руб.,	Коэффициент издержек на единицу продукции,
9 10 11 12	14,7 15 15,8 15,4	26,1 26,5 24,2 24,4	1255 1274 1305 1408	40,8 46,7 48,6 48,7

Для проведения корреляционного анализа используем стандартную офисную программу EXCEL. Для построения корреляционной матрицы воспользуемся инструментом КОРРЕЛЯЦИЯ настройки ПАКЕТ АНАЛИЗА (рис.2), запуск которого осуществляется следующим образом: Сервис Анализ данных Корреляция ОК.

Рис.2. Использование инструмента КОРРЕЛЯЦИЯ.

В диалоговом окне КОРРЕЛЯЦИЯ в поле Входной интервал необходимо ввести диапазон ячеек, содержащих исходные данные. Исходные данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек. Флажок Метки в первой строке – устанавливается в активное состояние, если выделены и заголовки столбцов. На рис. 3. показана экранная форма вычисления матрицы коэффициентов парной корреляции с помощью инструмента КОРРЕЛЯЦИЯ.

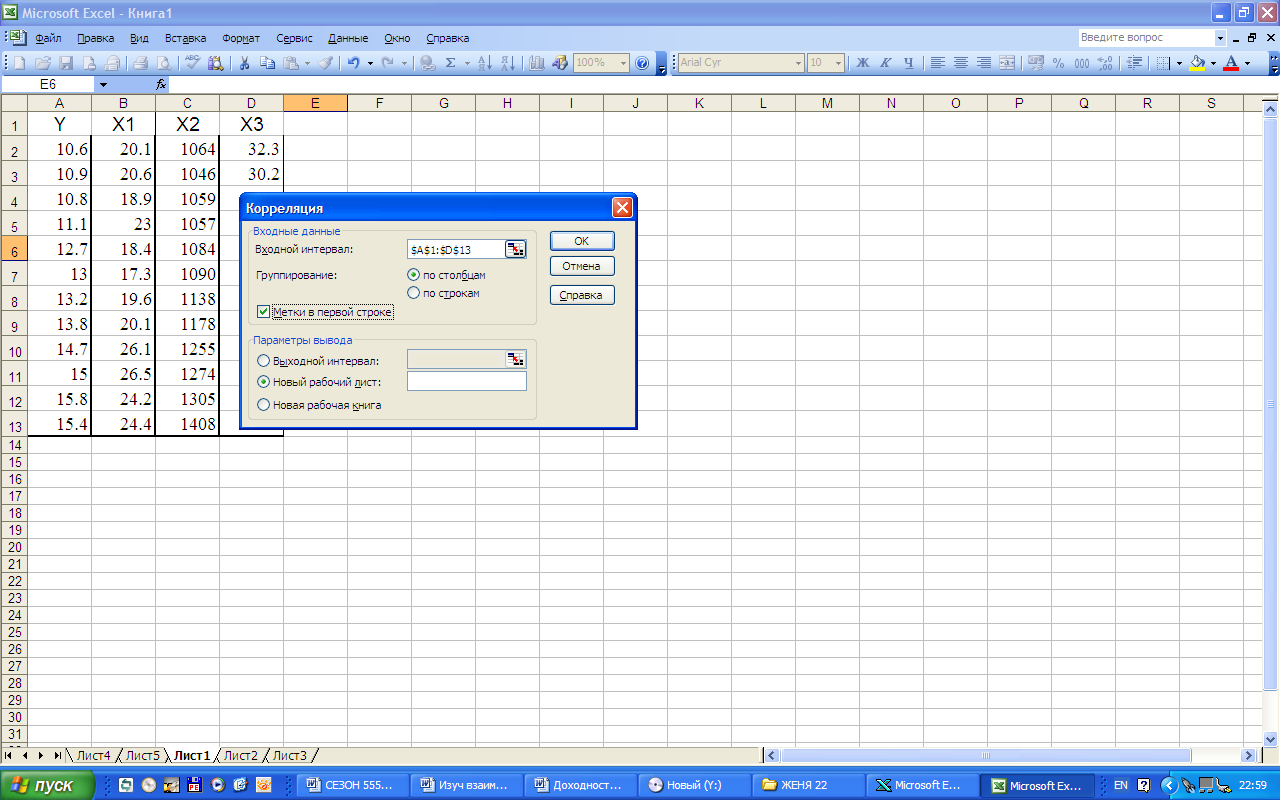
Рис. 3. Вычисление матрицы коэффициентов парной корреляции с помощью инструмента КОРРЕЛЯЦИЯ

Результатом работы инструмента Корреляция является таблица, содержащая рассчитанные линейные коэффициенты корреляции (рис.4).

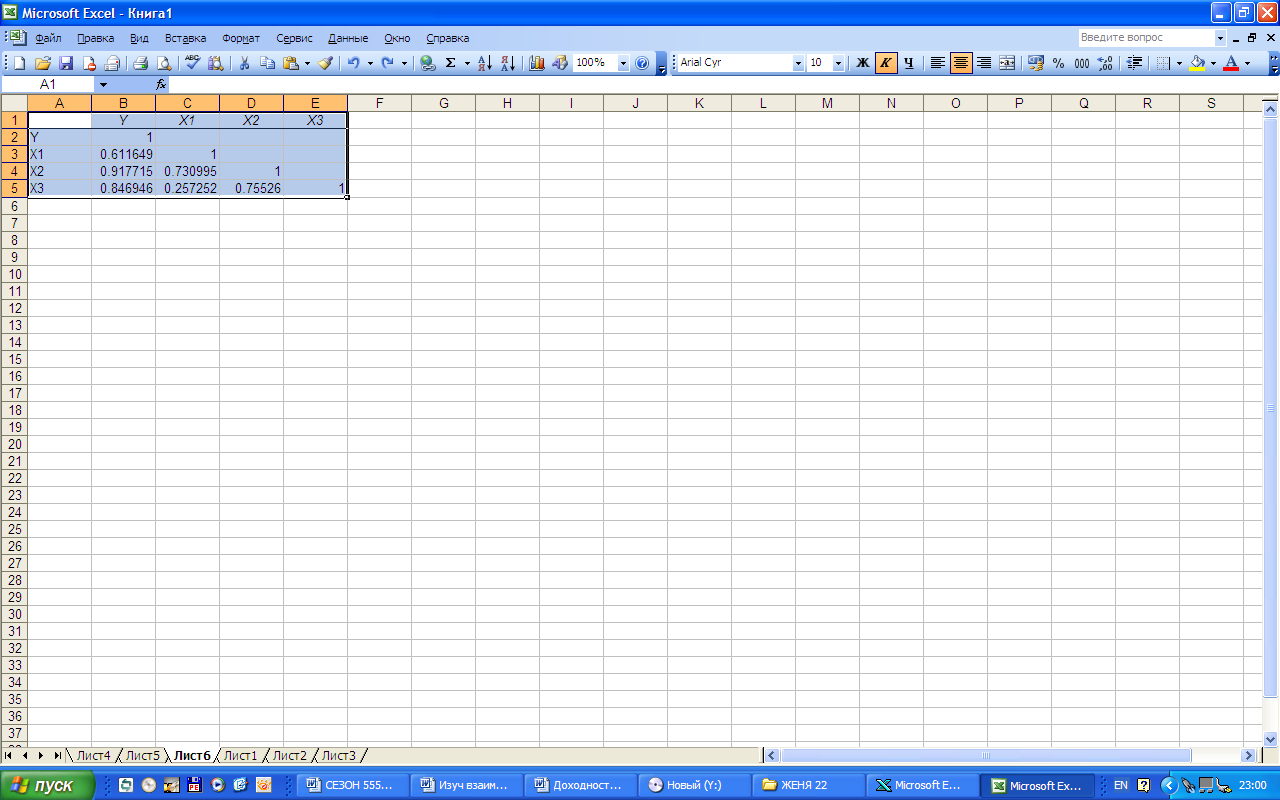
Рис. 4. Матрица коэффициентов парной корреляции

Результаты расчета в EXCEL приведены в таблице 3.

Таблица 3.

Матрица парных корреляций

Переменная	Y	X1	X2	X3
Y	1
X1	0,612	1
X2	0,918	0,731	1
X3	0,847	0,257	0,755	1

Оценку значимости коэффициента корреляции выполним с использованием t-критерия Стьюдента:

.

Для коэффициента корреляции :

.

Табличное значение критерия Стьюдента при уровне значимости α=0,05 и числе степеней свободы 10 равно 2,228. Так как , то полученное значение коэффициента корреляции признается значимым. Таким образом, делаем вывод, что между прибылью от реализации продукции и долей продаж существует статистическая взаимосвязь.

Аналогично проведем оценку значимости между остальными переменными.

Для коэффициента корреляции :

. Делаем вывод, что между прибылью от реализации продукции и отпускной ценой продукции существует статистическая взаимосвязь.

Для коэффициента корреляции :

. Делаем вывод, что между прибылью от реализации продукции и коэффициентом издержек существует статистическая взаимосвязь.

Наибольшее влияние на прибыль от реализации продукции оказывает отпускная цена продукции.

Корреляционное отношение определяется как отношение межгрупповой дисперсии к общей дисперсии:

,

где - межгрупповая дисперсия;

- общая дисперсия.

Дисперсии определяются по формулам:

, ,

где k – число групп;

- среднее значение результативного признака в j – группе;

- общая средняя результативного признака;

- число наблюдений в j–ой группе, , .

Применение корреляционного отношения возможно, если характер выборочных данных (количество, плотность расположение на диаграмме рассеивания) допускает, во-первых, их группирование по оси объясняющей переменной, и, во-вторых, возможность подсчета частных математических ожиданий внутри каждого интервала группирования.

Для определения эмпирического корреляционного отношения совокупность значений результативного признака разбивается на отдельные группы по определенному факторному признаку. Для каждой из этих групп вычисляются соответствующие групповые средние результативного признака. Взаимосвязь между факторным признаком и результативным проявляется в том, что с изменением факторного признака систематически возрастает или убывает среднее значение результативного признака. Например, группируя предприятия, производящие одну и ту же продукцию по техническому уровню производства (по уровню фондовооруженности) и вычислив для каждой группы среднюю выработку на одного работающего, можно установить наличие связи между названными факторами. Изменение групповых средних от группы к группе свидетельствует о наличии связи результативного признака с факторным признаком, а примерное равенство групповых средних – об отсутствии связи.

Величина корреляционного отношения принимает значения от 0 до 1. Близость ее к нулю говорит об отсутствии связи, близость к единице о тесной связи. В случае линейной связи величина эмпирического корреляционного отношения равна коэффициенту корреляции. Эмпирическое корреляционное отношение не может быть меньше коэффициента корреляции, что позволяет использовать величину разницу в качестве меры отклонения регрессионной зависимости от линейного вида.