§9. Формула полной вероятности. Формулы Байеса.

Одним из эффективных методов подсчёта вероятностей является формула полной вероятности, с помощью которой решается широкий круг задач.

Пусть событие A может наступить с одним и только одним из нескольких попарно несовместных событий Н₁, Н₂,…,Н_n, называемых гипотезами, т.е.

.

Так как Н₁, Н₂,…Н_n попарно несовместны, то несовместны и события АН₁, АН₂,…АН_n . Отсюда получаем, применяя формулы сложения и умножения вероятностей

Полученная формула

(1)

называется формулой полной вероятности.

Пример 1. (см. пример 1 §8). Из урны, в которой находятся m белых и n-m чёрных шаров, без возвращения выбираются два шара. Найдём вероятность события B={второй вынутый шар – белый},

Рассмотрим гипотезы: H₁= {первый вынутый шар – белый) и первый вынутый шар – чёрный}. Тогда По формуле полной вероятности получаем

Таким образом, мы получим

.

Аналогично можно установить, что вынимая последовательно без возвращения шары, мы получим одну и ту же вероятность вынуть белый шар на любом месте. Таким образом, при правильно организованной жеребьёвке, шансы всех участников одинаковы, независимо от того, в какой очерёдности они тянут жребий.

Замечание. Эту же задачу можно интерпретировать, как вычисление вероятности вытащить белый шар из урны, из которой был случайно утерян один или несколько шаров.

В тесной связи с формулой полной вероятности находятся так называемые формулы Байеса. Они относятся к той же ситуации, что и формула полной вероятности.

Поскольку событие А может наступить только вместе с одним из n попарно несовместных событий Н₁,…Н_{n ,} то найдём вероятность Р(Н_к | А) – вероятность того, что событие А наступит вместе с гипотезой Н_к.

По формуле умножения получаем

Откуда имеем

(2)

Или, если воспользоваться формулой полной вероятности (1) получим:

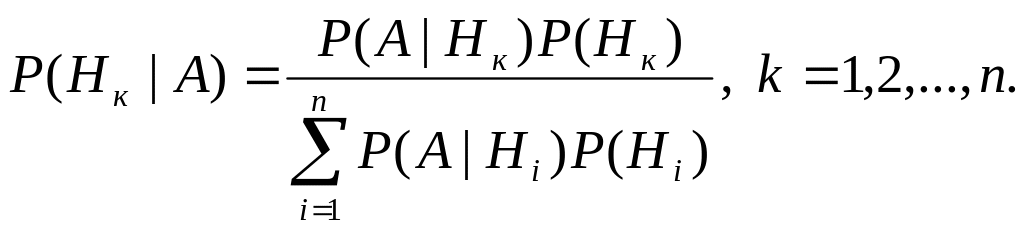(3)

Это и есть формулы Байеса.

Запомнить эти формулы нетрудно: в знаменателе стоит выражение для полной вероятности, а в числителе – одно из слагаемых (к-ое) в этом выражении.

Формулы Байеса можно интерпретировать следующим образом.

Пусть A – результат некоторого эксперимента,

Н_к – гипотезы. Вероятности Р(Н_к) – это априорные вероятности гипотез, вычисленные до проведения опыта, а условные вероятности Р(Н_к|А) – это апостериорные вероятности гипотез, вычисляемые после того, как стал известен исход эксперимента А. Формулы Байеса позволяют по априорным вероятностям гипотез и по условным вероятностям события А при гипотезах вычислять апостериорные вероятности Р(Н_к|А).

Пример 2. При обследовании больного имеется подозрение на одно из двух заболеваний Н₁ и Н₂. Их вероятности в данных условиях Р(Н₁ )=0,6, Р(Н₂ )=0,4. Для уточнения диагноза назначается анализ, результатом которого является положительная или отрицательная реакция. В случае болезни Н₁ вероятность положительной реакции равна 0,9, отрицательной – 0,1. В случае Н₂ положительная и отрицательная реакции равновероятны. Анализ провели дважды, и оба раза реакция оказалась отрицательной (событие А). Требуется найти вероятности каждого заболевания после проделанных анализов.

Решение. В случае заболевания Н₁ событие А происходит с вероятностью , а в случае заболевания Н₂ – с вероятностью . Следовательно по формуле Байеса имеем .

.

Отсюда видно, что полученные результаты анализов дают веские основания предполагать болезнь Н₂.