Гусева А.И. Дискретная математика: Математическая логика

Лекция 4

Операции над отношениями

Рассмотрим два отношения и на множестве М. [1].

Объединением двух отношений и называется новое бинарное отношение , элементы которого удовлетворяют следующему условию:

.

Пересечением двух отношений и называется новое бинарное отношение , элементы которого удовлетворяют следующему условию:

.

Композицией двух отношений и называется новое бинарное отношение , элементы которого удовлетворяют следующему условию:

.

Обращением бинарного отношения называется новое бинарное отношение, удовлетворяющее следующему условию .

Дополнением бинарного отношения до универсума называется новое бинарное отношение , .

Декартовым произведением двух бинарных отношений называется новое бинарное отношение, элементы которого удовлетворяют следующему условию

.

На рис. 1 приведены примеры операций над отношениями.

Замыкание отношения относительно свойства

Рассмотрим два отношения и на множестве М, обладает свойством S, . Отношение называется замыканием относительно свойства S тогда и только тогда:

• обладает свойством S ,

• является надмножеством ,

• - наименьшее.

Ядро отношения R на множестве M называется новое отношение R [R ^–1].

=

Рис. 1 Операции над отношениями

Используя свойства бинарных отношений, можно доказать следующую теорему [2].

Теорема

Пусть R бинарное отношение на М, . Тогда:

1. R рефлексивно тогда и только тогда, когда ,

2. R симметрично тогда и только тогда, когда

3. R транзитивно тогда и только тогда, когда

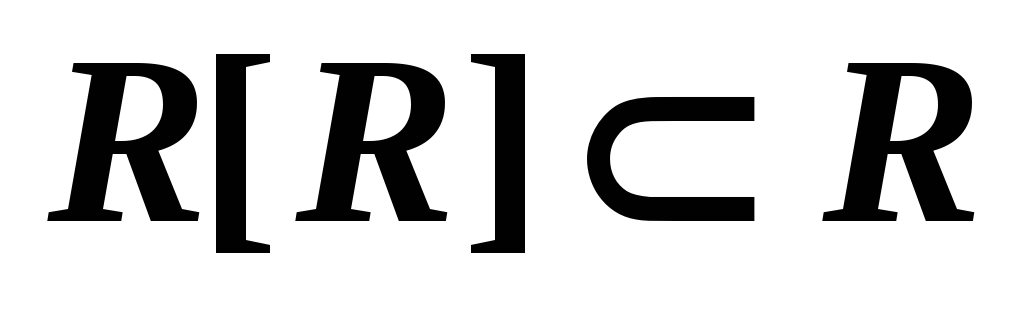
4. R антисимметрично тогда и только тогда, когда

5. R антирефлексивно тогда и только тогда, когда

6. R линейно тогда и только тогда, когда

ЛИТЕРАТУРА

.

1. М. Свами, К. Тхуласироман. Графы, сети и алгоритмы. – М.: Мир, 1984.

2. Ф.А. Новиков. Дискретная математика для программистов. - СПб.: Питер, 2001.