1.3. Задания для самостоятельной работы

Решить матричную игру, заданную платежной матрицей, сведя ее к паре двойственных задач линейного программирования. Предварительно произвести возможные упрощения платежной матрицы.

Вариант 1.

.

Ответ: p₁ = 0, p₂ = 0,17, p₃ = 0, p₄ = 0,83, p₅ = 0, q₁ = 0, q₂ = 0, q₃ = 0, q₄ = 0,83, q₅ = 0,17, цена игры = 1,83.

Вариант 2.

.

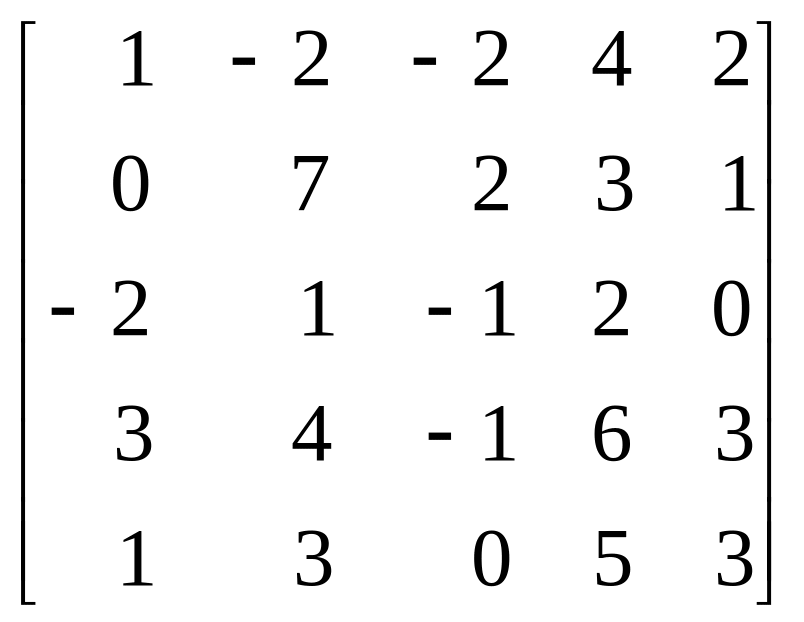Ответ: p₁ = 0, p₂ = 0,67, p₃ = 0, p₄ = 0,33, p₅ = 0, q₁ = 0,5, q₂ = 0, q₃ = 0,5, q₄ = 0, q₅ = 0, цена игры = 1.

Вариант 3.

.

Ответ: p₁ = 0, p₂=0,67, p₃ = 0,33, p₄ = 0, p₅ = 0, q₁ = 0, q₂ = 0, q₃ = 0,67, q₄ = 0,33, q₅ = 0, цена игры = 2,67.

Вариант 4.

.

Ответ: p₁ = 0, p₂ = 0, p₃ = 0,71, p₄ = 0,29, p₅ = 0, q₁ = 0, q₂ = 0,14, q₃ = 0, q₄ = 0,86, q₅ = 0, цена игры = 3,29.

Вариант 5.

.

Ответ: p₁ = 0, p₂ = 0,43, p₃ = 0,5, p₄ = 0, p₅ = 0,07, q₁ = 0,14, q₂ = 0,29, q₃ = 0,57, q₄ = 0, q₅ = 0, цена игры = 2,43.

Вариант 6.

.

Ответ: p₁ = 0,14, p₂ = 0, p₃ = 0, p₄ = 0,86, p₅ = 0, q₁ = 0,57, q₂ = 0, q₃ = 0,43, q₄ = 0, цена игры = 1,43.

Вариант 7.

.

Ответ: p₁ = 0, p₂ = 0,29, p₃ = 0, p₃ = 0,71, p₅ = 0, q₁=0,14, q₂ = 0,86, q₃ = 0, q₄ = 0, цена игры = 1,29.

Вариант 8.

.

Ответ: p₁ = 0, p₂ = 0,67, p₃ = 0,33, p₄ = 0, p₅ = 0, q₁ = 0,67, q₂ = 0,33, q₃ = 0, q₄ = 0, цена игры = 2,33.

Контрольные вопросы

1. Что такое игра? Какие бывают виды игр?

2. Поясните понятия “чистая стратегия”, “исход игры”, “платежная матрица”. Что значит решить матричную игру?

3. Принцип минимакса. Нижняя и верхняя цена игры.

4. Когда существует решение игры в чистых стратегиях? Что такое седловая точка матричной игры?

5. Как можно упростить платежную матрицу игры? Какие стратегии называются заведомо невыгодными?

6. Что такое смешанные стратегии игроков? Что означает решить матричную игру в смешанных стратегиях?

7. Что такое цена игры в случае решения задачи в чистых стратегиях? А в случае решения в смешанных стратегиях?

8. Поясните смысл неравенства     .

9. К решению каких задач линейного программирования сводится решение матричной игры?

10. Поясните, почему целевая функция задачи линейного программирования для игрока A должна быть минимизирована.

11. Какой должна быть платежная матрица игры, чтобы ее можно было свести к задаче линейного программирования?

Лабораторная работа 2. Решение статистических игр

2.1. Основные теоретические сведения

В экономической практике нередко приходится моделировать ситуации, придавая им игровую схему, в которых один из участников безразличен к результату игры. Такие игры называют статистическими, или играми с природой, понимая под термином “природа” всю совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решение.

В играх с природой степень неопределенности при принятии решения сознательным игроком возрастает. Объясняется это тем, что, если в стратегических играх каждый из участников постоянно ожидает наихудшего для себя ответного действия партнера, то “природа”, будучи безразличной в отношении выигрыша, может предпринимать такие ответные действия, которые выгодны сознательному игроку.

Поскольку игры с природой являются частным случаем парных матричных игр, то вся теория стратегических игр переносится и на игры с природой. Однако игры с природой обладают и некоторыми особенностями. Например, при упрощении платежной матрицы отбрасывать те или иные состояния природы нельзя, так как она может реализовать любое состояние независимо от того, выгодно это игроку А или нет. Другая особенность состоит в том, что решение достаточно найти только для игрока А, поскольку природа наши рекомендации воспринять не может. И еще одна важная особенность: в играх с природой смешанные стратегии имеют ограниченное (главным образом теоретическое) значение: не всегда можно для них найти форму, удобную для использования в реальной обстановке. Смешанные стратегии приобретают смысл при многократном повторении игры.

Игра с природой задается платежной матрицей, в которой строки соответствуют стратегиям игрока, а столбцы – состояниям “природы” (рис. 1.7).

	П1	…	Пn
A1	a11	…	a1n
…	…	…	…
Am	am1	…	amn
j	1	…	n

Рис. 1.7. Платежная матрица игры с природой

Кроме платежной матрицы, для игры с природой часто составляют матрицу рисков, которая во многих случаях позволяет более глубоко понять неопределенную ситуацию. Риском называется разность между максимально возможным выигрышем при данном состоянии природы и выигрышем, который будет получен при применении стратегии A_i в тех же условиях. Максимальный выигрыш в j-м столбце обозначим через _j, т. е. (величина _j характеризует благоприятность состояния природы). Риск игрока при применении им стратегии A_i в условиях П_j обозначим через r_ij. Тогда риск равен

r_ij = _j – a_ij ,

где r_ij  0.

Определение наилучшей стратегии сознательного игрока A в игре с природой основано на применении некоторых критериев для принятия решений. Применяются две группы критериев:

1. Критерии, основанные на известных вероятностях состояний природы. К этой группе относятся критерии Байеса и Лапласа.

2. Критерии, используемые в условиях полной неопределенности. Ко второй группе критериев относятся критерии Вальда, Сэвиджа и Гурвица.