29. Составные формулы

(Карташова А.)

30. Порядок выполнения логических операций

(Карташова В.)

Порядок выполнения логических операций в сложном логическом выражении:

1. инверсия

2. конъюнкция

3. дизъюнкция

4. импликация

5. эквивалентность

 Для изменения указанного порядка выполнения операций используются скобки.

 Логическое отрицание - ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным. Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО

F = A & B.Логическое умножение  КОНЪЮНКЦИЯ  - это новое  сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.

 F = A + B .Логическое сложение – ДИЗЪЮНКЦИЯ - это новое сложное выражение будет истинным тогда и только тогда, когда  истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ

 Логическое следование:  ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом  "следовательно"  и  выражается словами ЕСЛИ … , ТО …

Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"

 

31. Свойства логических операций

1.Коммутативность: x y = y x,  {&,  }.

Коммутативная операция — это бинарная операция  , обладающая коммутативностью (от позднелат. commutativus — «меняющийся»), то есть переместительностью:

для любых элементов  .

В частности, если групповая операция является коммутативной, то группа называется абелевой. Если операция умножения в кольце является коммутативной, то кольцо называется коммутативным.

Примеры:

• Сумма и произведение действительных чисел коммутативны:

• Конъюнкция и дизъюнкция коммутативны:

• объединение, пересечение и симметрическая разность множеств коммутативны:

• Возведение в степень действительных чисел, вообще говоря, некоммута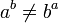тивно ( ) и даже не ассоциативно:

, но 

2. Идемпотентность: x x = x,  {&,  }.

Термин идемпотентность означает свойство математического объекта, которое проявляется в том, что повторное действие над объектом не изменяет его. Термин предложил американский математик Бенджамин Пирс (англ. Benjamin Peirce) в статьях 1870-х годов, произведя его от латинских слов idem («тот же самый») и potens («способный»).

Операция:

Идемпотентная операция в математике — бинарная операция, относительно которой всякий элемент обладает идемпотентностью в вышеназванном смысле:

.

Идемпотентная операция в информатике — действие, многократное повторение которого не приводит к изменениям иным, нежели при однократном. Примером такой операции могут служить GET-запросы в протоколе HTTP. По спецификации сервер должен возвращать одни и те же ответы на идентичные запросы (при условии что ресурс не изменился между ними по иным причинам). Такая особенность позволяет кэшировать ответы, снижая нагрузку на сеть.

Идемпотентная операция — это бинарная операция, обладающая идемпотентностью:

 для любого элемента  .

3. Ассоциативность: (x y) z = x (y z),  {&,  }.

Ассоциативность (от лат. associatio — соединение)

• В математике (также сочетательность) — свойство любой операции  , такое что для неё выполняется равенство:

 для любых элементов  .

Например, для умножения:  .

• В программировании (также очерёдность) ассоциативностью операторов называют последовательность их выполнения (или направление вычисления), реализуемое, когда операторы имеют одинаковый приоритет и отсутствует явное (с помощью скобок) указание на очерёдность их выполнения. При этом различается левая ассоциативность, при которой вычисление выражения происходит слева-направо, и правая ассоциативность — справа-налево. Соответствующие операторы называют левоассоциативными и правоассоциативными.

4. Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:

• ,

• ,

• .

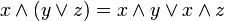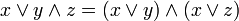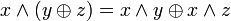Дистрибути́вность (от лат. distributivus — «распределительный»), также распределительность^{[источник не указан 316 дней]} — свойство согласованности двух бинарных операций, определённых на одном и том же множестве.

Говорят, что две бинарные операции + и × удовлетворяют свойству дистрибутивности, если для любых трех элементов  :

 — дистрибутивность слева;

 — дистрибутивность справа.

Если операция × является коммутативной, то свойства дистрибутивности слева и справа совпадают. Аддитивная и мультипликативные операции в кольцах и полях по определению удовлетворяют свойству дистрибутивности.Если операции сложения и пересечения для односторонних идеалов некоторого кольца (или подмодулей некоторого модуля) удовлетворяют свойству дистрибутивности, то говорят одистрибутивном кольце (или дистрибутивном модуле).

5. Законы де Мо́ргана:

,

.

Законы де Мо́ргана (правила де Мо́ргана) — логические правила, связывающие пары дуальных логических операторов при помощи логического отрицания.

Определение:

Огастес де Морган первоначально заметил, что в классической пропозициональной логике справедливы следующие соотношения:

not (P and Q) = (not P) or (not Q)

not (P or Q) = (not P) and (not Q)

Обычная запись этих законов в формальной логике:

или

в теории множеств:

или:

Если существует операция логического умножения двух и более элементов, операция «и» — (A&B), то для того, чтобы найти обратное от всего суждения ~(A&B), необходимо найти обратное от каждого элемента и объединить их операцией логического сложения, операцией «или» — (~A+~B). Закон работает аналогично в обратном направлении: ~(A+B) = (~A&~B)