
- •1. Алфавит, слова, операции над словами
- •2. Языки. Операции над языками
- •3. Абстрактные формальные системы
- •4. Формальные порождающие грамматики
- •5. Классификация грамматик
- •Диаграмма грамматики.
- •Порождение и распознавание цепочек.
- •Детерминизация конечных автоматов
- •Автоматы с - переходами.
- •9. Минимизация числа состояний автомата
- •9.1. Лингвистический автомат.
- •9.2. Метод Хафмена.
- •Регулярные множества и регулярные выражения.
- •Разрешимые проблемы для а-грамматик
- •7. Нотации для задания кс-грамматик.
- •8. Структура цепочек. Су-схемы
- •9. Преобразования грамматик.
- •10. Разрешимые и неразрешимые свойства кс-грамматик
- •11. Синтаксический анализ для кс-языков
- •11.1 Ll(k)-грамматики
- •12.Элементы теории конечных автоматов
- •13.Сети автоматов. Их анализ и синтез.
Порождение и распознавание цепочек.
Конечный автомат (автомат Мили)S=<Va,Q,Vb,q0,F,G>, где
Va={a1,a2,…am},m1 – входной алфавит автомата,
Vb= {b1,b2, …,bn},n1 – выходной алфавит автомата,
Q= {q0,q1,…qk},k0 – внутренний алфавит (алфавит состояний),
q0Q– начальное состояние автомата,
F- функция переходов;F:QVaQ,
G- функция выходов,G:QVaVb.
Автомат однозначно задает отображение Va*Vb* (входной цепочки в выходную).
Пример автомата:
Пусть Va=Vb= {a,b},Q= {A,B},q0=A. Функции переходов и выходов могут быть заданы в функциональной форме:
|
F(A, a) = A |
G(A, a) = a |
|
F(A, b) = B |
G(A, b) = a |
|
F(B, a) = A |
G(B, a) = b |
|
F(B, b) = B |
G(B, b) = b |
Либо в виде объединенной таблицы входов-выходов, в которой по столбцам указаны исходные состояния, во строкам – входы, в соответствующей ячейке через запятую указываются состояние, в которое переходит автомат и соответствующий выходной сигнал.
|
|
A |
B |
|
a |
A, a |
A, b |
|
b |
B, a |
B, b |
Диаграмма (граф переходов автомата), представляющая этот автомат, изображена на рис. 3.
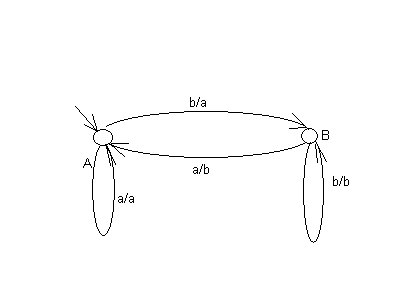
Рис. 3
Диаграмма автомата похожа на диаграмму грамматики. Отличие состоит в том, что есть некоторый выход, не выделены конечные состояния.
Если убрать выходы и ввести конечные состояния, то получится автомат, который не преобразует, а либо распознает, либо порождает цепочки – лингвистический автомат.
Лингвистический автомат– этоSL= <Q,VT,q0,F,K>,
где Q= {q0,q1,…qk},k0 – множество состояний автомата (внутренний алфавит),
VT ={a1,a2,…am},m1– множество терминальных символов (внешний алфавит) автомата,
q0 – начальное состояние автомата,q0 Q,
F:QVTQфункция переходов,
KQ– множество конечных(заключительных) состояний.
Рассмотрим автомат как распознающий, тогда ему соответствует следующая абстрактная модель:
Входная лента, на которой расположена анализируемая цепочка, считывающая(входная) головка и устройство управления.
На каждом шаге обозревается ровно один символ. Пара (q,a), гдеa- обозреваемый символ, аq- состояние автомата, называется ситуацией автомата. Если автомат находится в ситуации(qi,aj) и F(qi, aj)=qk, то считывающая головка перемещается на один символ вправо, автомат переходит в состояниеqk. Получаемая ситуация(qi,aj+1) (обозревается следующий символ на ленте. Если жеF(qi, aj) не определена, то входная цепочка не допускается автоматом.
Если в результате прочтения входной цепочки автомат окажется в заключительном состоянии, то говорим, что автомат допустил цепочку.
Более строго:
В начале работы автомат находится в состоянии q0, на входе – цепочкаa1,a2,…,an, обозревается самый левый символ цепочки ситуация (q0,a1) , затем переход в некоторую ситуацию (qi,a1),…, (qj,an), и, наконец, в ситуацию (qs,) &qsK. Назовём конфигурацией автомата паруH=(q,x), гдеq—текущее состояние автомата;x—остаток входной цепочки, самый левый символ которой обозревается входной головкой. Конфигурация, очевидно, определяет и ситуацию. Говорят, что конфигурация (p,x1) получена из конфигурации (q,x) за один такт (обозначается (q,x)├(p,x1) ), еслиx=ax1иF(q,a)= p.
. Если H0,H1,…,Hn(n1) - последовательность конфигураций, таких, чтоHi ├Hi+1 ,i{1,…,n}, то, как и раньше, будем использовать обозначенияH0 ├+Hn илиH0 ├*Hn если справедливоH0 ├+Hn H0=Hn.
Пусть x— анализируемая цепочка. Начальная конфигурация имеет вид (q0,x) заключительная – (qs,),qsF. Говорят, что автомат A допустил цепочкуx, если (q0,x)├* (q,) иqF(Использование отношения├* позволяет включить в множество допускаемых цепочек и пустую цепочку, еслиq0F.
Языком L(A), допускаемым конечным автоматомA, называется множество допускаемых им цепочек
L(A) = { x / (q0, x) ├ * (q, ) & q K}.
Диаграмма лингвистического автомата отличается от диаграммы автомата Мили выделением конечных состояний и отсутствием выходов.
Например, для лингвистического автомата SA= <Q, {a,b,c},q0,F, {q1}>, функция переходов которого
F(q0,c)=q0,
F(q0,a)=q1,
F(q1, b)= q1,
диаграмма представлена на рис. 4.
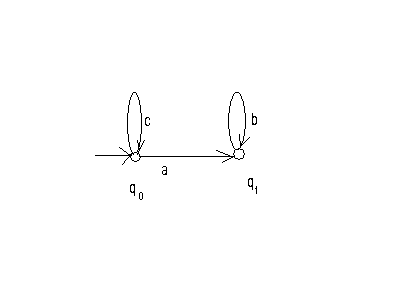
Рис.4
Язык, распознаваемый этим автоматом L(SA)= {cnabm,n,m0}.
Цепочка не распознается автоматом, если или нет перехода по читаемому символу, или в результате прочтения цепочки состояние, в которое перешел автомат - не конечное.
Процесс допускания цепочки соответствует движению по графу. Цепочка допущена, если существует путь из начальной вершины в заключительную, при котором последовательно выписанные метки проходимых дуг составляют анализируемую цепочку.
Граф автомата в силу тождественности его структуры с диаграммой грамматик всегда может рассматриваться как диаграмма некоторой грамматики, роль нетерминальных символов в которой будут играть метки состояний автомата. Нетрудно видеть, что грамматика, полученная по графу переходов автомата, при интерпретации последнего как ее диаграммы будет порождать тот же самый язык, который допускается автоматом. В обоих случаях язык однозначно определяется множеством путей из начальной вершины в заключительные, а множество путей совпадает, так как граф один и тот же. Таким образом, по любому конечному автомату может быть построена эквивалентная А-грамматика и, следовательно, абстрактно взятый ориентированный граф с помеченными вершинами и дугами, в котором выделена начальная и множество заключительных вершин и удовлетворяются требования однозначности отображения F, может рассматриваться и как диаграмма грамматики и как граф переходов автомата - все дело в интерпретации.
По диаграмме автомата всегда легко построить эквивалентную грамматику (автомат по грамматике строить сложнее, так как в грамматике одному символу входного алфавита может соответствовать более одного перехода см., например, рис. 2.
Правила грамматики по диаграмме автомата строится следующим образом:
Каждому состоянию автомата сопоставляем нетерминал грамматики.
Каждому переходу, соответствующему из состояния Pпо терминалуaв состояниеQсопоставляется правило грамматикиPaQ.
Каждому конечному состоянию Rсопоставляется правилоR.
Начальному состоянию автомата сопоставляется начальный символ грамматики.
Например, автомату, диаграмма которого представлена на рис.4, соответствует грамматика G10 с правилами
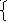 S
cS a
A
S
cS a
A
A b A
где состоянию q0сопоставлен нетерминалS, а состояниюq1- нетерминалA.
Таким образом, состояния конечного автомата однозначно отображаются в нетерминалы грамматики.
Однако, если мы рассмотрим грамматику G11 cправилами
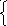 S
a S a
A
S
a S a
A
A b Ab K
K,
диаграмма которой представлена на рис. 5
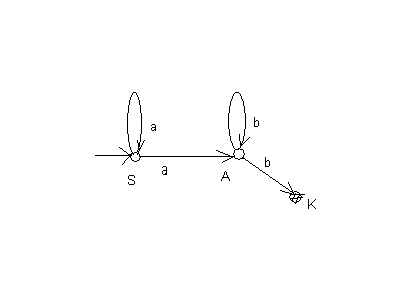
Рис.5
Однозначность нарушается неоднозначностью переходов, допускаемых в грамматиках.
