5. Классификация грамматик

Выделяются определенные классы грамматик, основными среди которых являются контекстно-свободные (КС), контекстно-зависимые (КЗ), автоматные…

Основными типами грамматик являются:

Грамматики класса «0» - не накладывается ограничений на вид правила.

Контекстно-зависимые (КЗ) – грамматики, все правила которых имеют вид , где,(V_TV_N )*

Например, грамматика G₄ с правилами

S  abA ab bA  Ab aA  aabA aA  aab

Контекстно-свободные (КС- грамматики), все правила которых имеют вид А, где АV_N,(V_TV_N )*.

Например, грамматика G₅с правиламиSaАbab.

L(G₅) = L(G₄)

Автоматные (А-грамматики), все правила которых имеют вид Аа, Аa B, А, aV_T, A,B V_N.

Иногда выделяется еще один класс грамматик: контекстные грамматики, или грамматики класса 1, все правила которых имеют вид , где,(V_TV_N),A V_N,(V_TV_N )*.

Здесь пара цепочек исоставляет неизменяемый контекст правила. Между контекстными грамматиками и КЗ-грамматиками существует взаимно-однозначное соответствие, не всегда очевидное. По выразительной мощности эти классы грамматик совпадают, однако, поскольку для одного и того же языка контекстная грамматика содержит большее число правил, мы будем изучать именно КЗ-грамматики.

Пример.

Грамматика G₆, КЗ-грамматика

S aAc A aABc A b bBbb cB Bc

L(G6)= {anbncn, n

Эквивалентная ей контекстная грамматика G₇. В ней правило переноса символа С заменяется на 3 правила.

S ABC B ABDC B b bDbb CD ED ED EC EC DC Cc

L(G7)= {anbncn, n

В соответствии с классом грамматики, порождающей язык, классифицируются языки. Т.Е. язык, для которого может быть порожден КС- грамматикой, называется КС-языком (т.е. язык, для которого существует порождающая его КС-грамматика, и не существует А-грамматики, порождающей этот язык).

А-язык - язык, для которого может быть построена порождающая его А-грамматика.

КЗ-язык – язык, который может быть построен только КЗ-грамматикой.

Непосредственная классификация грамматик выглядит следующим образом.

Класс А-грамматик включается в класс КС-грамматик. Все грамматики принадлежат классу 0.

Однако класс КС-грамматик не включается в класс КЗ-грамматик, так как правила вида Амогут принадлежать КС-грамматикам, но не КЗ-грамматикам, т.к.А.

Поэтому общий вид классификации следующий:

Класс 0

КЗ-грамматики

КС-грамматики

КС-грамматики без -правил

А-грамматики без

-правил

А-грамматики

Для рассмотрения иерархии языков надо больше знать о преобразованиях грамматик.

6. А-языки. Конечные автоматы.

Диаграмма грамматики.

Пусть дана А-грамматика G=< V_T,V_N, S, R>. Диаграмма А-грамматики – граф с помеченными вершинами и дугами. Множество вершин графа соответствует множеству нетерминалов А-грамматики, приведенной к каноническому виду, а множество дуг – множеству правил грамматики.

Преобразование грамматики:

Вводим дополнительный нетерминальный символ К. V_N =V_NК

Заменяем правила вида Аа на правила АаК.

Вводим дополнительное правило К

Таким образом, все правила грамматики теперь приобрели "стандартный" вид AaB илиA.

Построение диаграммы опишем следующими правилами.

1. Каждому нетерминальному символу поставим в соот­ветствие вершину и пометим ее этим символом.

2. Каждому правилу AaB сопоставим дугу из верши­ныAв вершинуВи пометим ее терминальным символома.

3. Отметим в графе как начальную вершину - вершину, со­ответствующую начальному символу, и как заключительные - все такие вершины В, чтоB (на диаграмме используется символ #) .

Пример. Пусть грамматикаG₈ описывается правилами:

S aBbC B bbB C aS

Грамматика в канонической форме будет иметь вид:

S aBbC B bKbB C aS K

Диаграмма грамматики приводится на рис.1.

Рис.1

Очевидно, что существует взаимно-однозначное соответсвие между грамматикой в каноническом виде и диаграммой.

Например, рассмотрим диаграмму грамматики, представленную на рис.2.

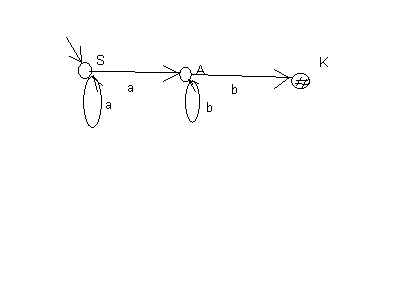
Рис.2

Очевидно, что диаграмме соответствует грамматика G₉с правилами

S aSaB B bKbB K 