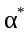- •Компиляция. Основные понятия. Контекст компилятора
- •Этапы, фазы и проходы
- •Фаза анализа. Основные понятия.
- •Фаза синтеза. Основные понятия.
- •Методы определения языка
- •Понятие регулярных выражений
- •Понятие грамматики
- •8.Иерархия грамматик по Хомскому
- •9 . Порождения синтаксические деревья
- •Неоднозначность
- •11.Понятие лексического анализа
- •12.Лексический анализ с помощью регулярных выражений
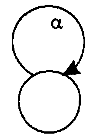
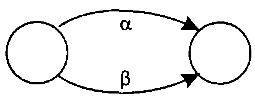
- •Лексический анализ с помощью конечных автоматов
- •14. Лексический анализ с помощью Lex
- •15. Нисходящий анализ. Критерии принятия решений.
- •16. Понятие ll(1)-грамматики
- •17. Рекурсивный спуск. Расширенная форма записи правил для исключения рекурсивных вызовов.
- •18. Рекурсивный спуск. Комбинирование рекурсии и итерации.
- •19. Преобразование грамматик. Удаление левой рекурсии
- •20. Преобразование грамматик. Факторизация
- •21. Введение действий в грамматику
- •22. Восходящий синтаксический анализ. Основные понятия. Критерий принятия решений
- •Восходящий синтаксический анализ. Таблица синтаксического анализа.
- •25. Характеристический конечный автомат.
- •Восходящий синтаксический анализ. Slr(1), lalr(1), общий алгоритм формирования таблицы lr(1)-анализа.
- •Восходящий синтаксический анализ. Генератор восходящих анализаторов yacc. Основные понятия.
- •Семантический анализ. Не-контекстно-свободные характеристики языков.
- •Семантический анализ. Таблица символов.
- •Семантический анализ. Таблица типов.
- •31.Семантический анализ. Таблицы функций. Таблицы меток
- •32. Распределение памяти. Классификация памяти
- •33. Распределение памяти. Стек времени выполнения. Определение области видимости.
- •34. Распределение памяти. Стековый фрейм.
- •35. Распределение памяти. Дисплей.
- •35. Адреса времени компиляции. Простые адреса. Адресация элементов статического массива.
- •37. Распределение памяти. Адреса времени компиляции. Адреса динамического массива
- •38. Куча. Основные понятия. Методы автоматического освобождения памяти.
Понятие регулярных выражений
Регулярные выражения
Р ассмотренные
языки можно также определить с помощью
регулярных
выражений, подобных
приведенному ниже.
ассмотренные
языки можно также определить с помощью
регулярных
выражений, подобных
приведенному ниже.
* - звездочка (замыкание) Клини. Если в
каждой строке языка должно находиться
минимум по одному элементу х
и у,
то язык можно определить следующим
образом.
- звездочка (замыкание) Клини. Если в
каждой строке языка должно находиться
минимум по одному элементу х
и у,
то язык можно определить следующим
образом.

или альтернативно
В регулярных выражениях можно использовать
символ "|" (читается как "или").
Таким образом, выражение
представляет запись языка, стоки которого
состоят из нуля или большего количества
элементов х
или из нуля
или большего количества элементов у.
регулярных выражениях можно использовать
символ "|" (читается как "или").
Таким образом, выражение
представляет запись языка, стоки которого
состоят из нуля или большего количества
элементов х
или из нуля
или большего количества элементов у.
Ч тобы
более формально определить понятие
регулярного выражения, введем вначале
понятие алфавита.
Алфавит
представляет собой конечный набор
символов, подобный приведенным ниже.
тобы
более формально определить понятие
регулярного выражения, введем вначале
понятие алфавита.
Алфавит
представляет собой конечный набор
символов, подобный приведенным ниже.
Если А — алфавит, то к числу регулярных выражений
относятся:
нулевая строка (обозначается ε);
любой элемента А.
Кроме того, если Р и Q являются регулярными выражениями, то регулярными являются также следующие выражения.
PQ (Q следует после Р)
P|Q (Р или Q)
Р* (нуль или более вхождений Р)
+ - не является оператором регулярных выражений.
П римеры
регулярных выражений:
римеры
регулярных выражений:
КА и регулярные выражения
|
|
|
|
|
|
Понятие грамматики
Язык
 невозможно определить посредством
регулярного выражения, поскольку в
регулярных выражениях не существует
возможности указать, что количество
элементов х
должно
равняться количеству элементов у.
невозможно определить посредством
регулярного выражения, поскольку в
регулярных выражениях не существует
возможности указать, что количество
элементов х
должно
равняться количеству элементов у.
Решение – использование продукций как нижеследующие
 - «имеет вид» или «может иметь вид»
- «имеет вид» или «может иметь вид»
Продукции могут использоваться для генерации строк языка с использованием следующих правил.
1. Начать с символа S и заменить его строкой, расположенной справа от знака, продукции.
2. Если полученная строка не содержит больше символов S, она является строкой языка. В противном случае следует снова заменить S строкой после знака продукции, а затем снова вернуться к п. 2.
П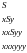 оследовательность
строк
оследовательность
строк
м ожно
заменить на
ожно
заменить на
- читается как «порождает»
Последовательность шагов, использованная для генерации строки
с применением продукций грамматики, называется порождением
(


 derivation)
строки.
derivation)
строки.
Грамматика используется для генерации последовательностей символов, составляющих строки языка, начиная с аксиомы и последовательно заменяя ее (или нетерминалы, которые появятся позднее) с помощью одного из порождений грамматики. На каждом этапе к нетерминалу из левой части применяется продукция, заменяющая этот нетерминал последовательностью символов своей правой части. Процесс прекращается после получения строки, состоящей только из терминальных символов (т.е. не содержащей нетерминалов). Языку принадлежат те, и только те строки символов, которые можно получить с помощью заданной грамматики.
Например, грамматикой для языка будет грамматика


 Где
Где
грамматикой для языка
б удет
грамматика
удет
грамматика
г де
де
Рассмотрим порождение строки xxyyy

Каждая из строк, фигурирующих в порождении, называется сентенциальной формой, а последняя строка (состоящая только из терминалов) называется предложением языка.
Использование символа "=>" между двумя сентенциальными формами
о


 бозначает,
что строка справа от этого символа
получена из строки слева от него
посредством одного порождения. В то же
время можно записать
бозначает,
что строка справа от этого символа
получена из строки слева от него
посредством одного порождения. В то же
время можно записать
Условимся, что последовательность продукций (порождения)

 можно
записать в сжатой форме
можно
записать в сжатой форме
Н еобходимо отметить, что для генерации конкретного языка обычно не существует единственной грамматики. На тривиальном уровне любой нетерминал можно заменить еще неиспользованным символом. Можно произвести более значительные изменения: изменить форму и количество продукций. Рассмотрим следующий язык.
Д анный
язык можно сгенерировать, используя
такой набор продукций.
анный
язык можно сгенерировать, используя
такой набор продукций.
Этот набор отличается от приведенного ранее для того же языка.
Две грамматики генерирующие один и тот же язык называются эквивалентными. Иногда при создании компилятора оказывается полезным или даже необходимым заменить данную грамматику эквивалентной.
Данное определение грамматики допускает грамматики
более общих типов чем те, что были приведены в качестве примеров.
Например, левая часть продукции не обязательно должна состоять
из одного символа. Рассмотрим следующую грамматику.

Г де
де
Продукции называются контекстно-зависимыми. Типичные порождения для данной грамматики могут иметь вид