37. Распределение памяти. Адреса времени компиляции. Адреса динамического массива
Для языков с динамическими границами (до выполнения программы они неизвестны) шаги по индексам можно найти после объявления массива и занесения его в стек, что опять же уменьшит количество вычислений, выполняемых при каждом обращении к массиву. Хотя значения шагов по индексам в процессе компиляции могут быть неизвестны, практически всегда будет известен объем памяти, которую будут занимать шаги по индексам, и память для них может быть выделена в процессе компиляции. В то же время память для самих элементов массива может выделяться только при выполнении программы, поскольку при компиляции значения границ могут быть неизвестны.
Для рассмотрения динамических массивов требуется более общая модель стека времени выполнения, чем рассмотренная ранее. В общем случае неизвестно расположение начала массива в стековом фрейме. Поэтому каждый стековый фрейм удобно разбить на две части: статическую часть, в которой содержатся значения, известные во время компиляции, и динамическую часть, содержащую значения, неизвестные в процессе компиляции. Все значения динамической части можно будет получить (с помощью указателей) из | значений статической части
С другой стороны, в динамической части фрейма будут находиться элементы массива. При использовании этой модели на практике даже элементы массива со статическими границами будут храниться в динамической части фрейма. Описанная более общая модель стекового фрейма изображена на рисунке.
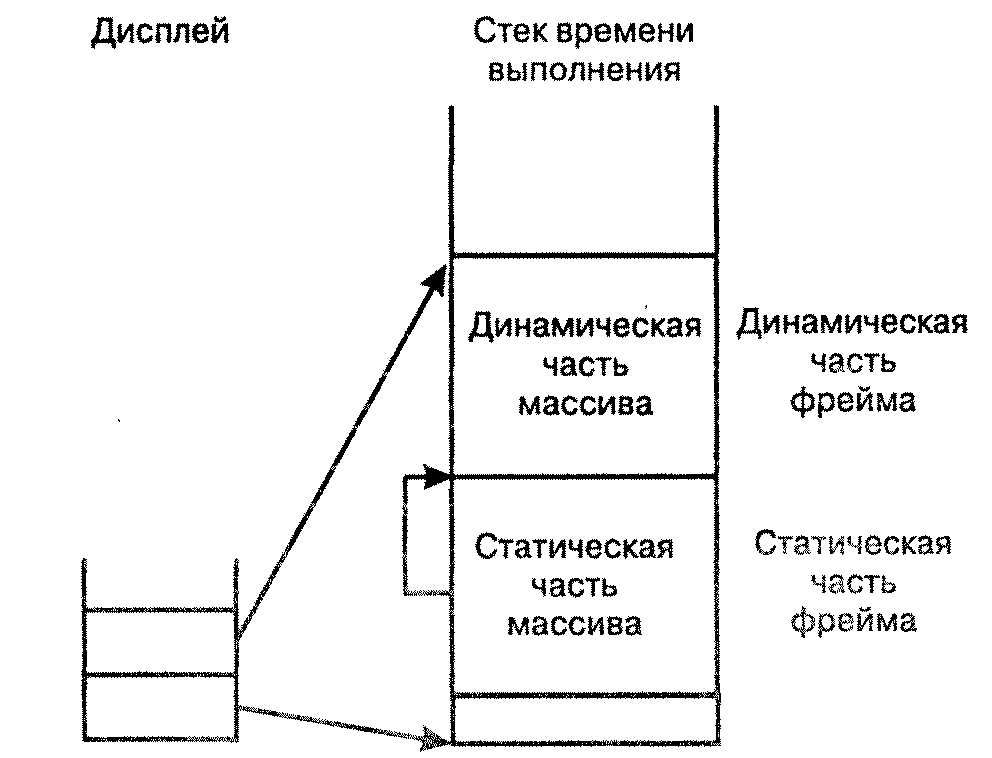
В этой модели для доступа к элементам массива (по сравнению с доступом к элементам, не входящим в массив) необходимы дополнительный; указатель и офсет. Значение номера уровня фрейма дает первый указатель с дисплея. К этому добавляется офсет указателя (в статической части массива) относительно начала массива, кроме того, во время выполнений программы данный указатель увеличивается, чтобы представлять адрес конкретного элемента массива.
В процессе компиляции адрес массива в целом – это просто уровень и офсет, соответствующий началу статической части массива. Для нахождения адреса во время выполнения требуются вычисления, общий вид которых приведен ранее. Очевидно, что доступ к элементам массива занимает много времени, в особенности для многомерных массивов. Это время можно уменьшить, если производить вычисление шагов по индексам только один раз. Для массивов с динамическими границами при выполнении программы время также тратится на каждое обращение к дополнительному указателю.
38. Куча. Основные понятия. Методы автоматического освобождения памяти.
Куча используется для хранения значений, к которым может потребоваться доступ от момента выделения для них памяти и до завершения программы. Не существует механизма языка, подобного выходу из блока или функции, который сделает область памяти недоступной. На первый взгляд схема распределения для такой памяти должна выделять память от одного конца линейного пространства до другого, пока свободная память не будет распределена полностью. Может показаться, что при этом никаких проблем с перераспределением или чрезмерным использованием памяти возникнуть не должно. В то же время данный подход имеет существенный недостаток, а именно: после первого полного распределения памяти применение следующего оператора, например,
string = malloc(4);
который попытается выделить четыре бита памяти и вернуть указатель на эту область, вызовет ошибку в программе.
Впрочем, прежде чем смириться с этим, следует вспомнить, что область памяти может стать недоступной вследствие таких операций программы, как переназначение указателей и т.д. Например, выделенное ранее пространство может стать недоступным для переменной string после следующего присваивания.
string = newstring;
В то же время данная операция позволяет получить доступ к рассматриваемому пространству некоторой другой переменной. Рассмотрим результат выполнения присваивания
stringl = string;
между двумя указанными выше операторами. Считая, что другие операторы, связанные с данными, отсутствуют, подобные действия приведут к тому, что переменной stringl будет доступно пространство, выделенное оператором malloc.
Поскольку, в общем случае, в процессе компиляции неизвестно, как будет выполняться программа, то при компиляции невозможно узнать, когда станет недоступной память, выделенная оператором malloc. Это означает, что код для восстановления области кучи не может быть сгенерирован в процессе компиляции, хотя недоступными могут стать большие области, выделенные в куче. Один из способов преодоления такой трудности заключается в том, чтобы программисты (исходя из своих знаний о том, как будет выполняться программа) предугадывали момент, когда память кучи становится недоступной, и вводили в исходный код явные инструкции для перераспределения памяти. Например, в С для освобождения области памяти, отведенной переменной string, можно записать следующее.
free(string);
В то же время данный подход требует от программиста большого профессионализма и ответственности. Итак, какие-либо автоматизированные методы освобождения памяти применять нежелательно. В языке Java предполагается, что ответственность за освобождение недоступной памяти должна возлагаться на реализацию Java, а не на программиста; таким образом, любая реализация Java должна иметь соответствующие механизмы. Примечательно, что в отличие от ранее описанных моделей пмяти, Java сохраняет в куче массивы. Все объекты также хранятся в куче.
В связи с восстановлением недоступных областей памяти существуют два возможных метода управления кучей.
1)сборка мусора (garbage collection);
2)использование счетчиков ссылок (use of reference counters).
Первый метод, пожалуй, является более популярным, но и более необходимым. Преимущество этого подхода заключается в том, что до полного распределения всего доступного пространства памяти не возникает потребности в восстановлении любой его части. Вследствие этого во многих случаях для сборки мусора времени вообще не требуется. Если (и когда) сборка мусора все-таки требуется, этот процесс происходит в две фазы.
Фаза маркировки, в которой (посредством введения значений в битовую карту) помечается память кучи, доступная для переменных программы.
Фаза сжатия, в которой все доступное пространство сдвигается в один конец кучи, а память, подлежащая повторному использванию, образует непрерывный блок в другом конце кучи. При этом, разумеется, следует аккуратно проверить, чтобы соответствующим образом изменились все значения указателей.
Из этих двух фаз фаза маркировки наиболее интересна и допускает меньше альтернативных способов реализации. Требуются некоторые средства “маркировки” ячеек памяти, к которым при необходимости могут обращаться переменные программы. Для этого может использоваться битовая карта с достаточным числом битов для сопоставления с каждой ячейкой кучи. Битовая карта не является частью кучи и располагается отдельно от нее. Каждый бит в битовой карте может принимать одно из двух значений.
0 – соответствующая ячейка памяти не доступна для переменных программы.
1 – соответствующая ячейка памяти доступна для переменных программы.
В начале процесса сборки мусора все элементы битовой карты имеют значение 0, а при выполнении алгоритма различным элементам карты присваивается значение 1. В завершение сборки мусора значение 1 получат все элементы битовой карты, которые соответствуют ячейкам памяти, доступным для переменных программы. Простой алгоритм сборки мусора использует стек (называемый стеком сборки мусора) и заключается в следующем.
Сборка мусора 1
1. Стек времени выполнения линейно просматривается, пока не будет обнаружена переменная, указывающая на непомеченную ячейку кучи. Это может быть или собственно переменная, которая является указателем (в кучу), или компонент записи, который является указателем. В дальнейшем, все ячейки кучи, на которые указывают подобные переменные, маркируются посредством включения соответствующих бит в битовую карту.
2. Некоторые ячейки, в свою очередь, могут быть указателями на непомеченные ячейки кучи. В этом случае их адреса помещаются в стеке сборки мусора.
3. Далее следуют адреса с верха стека сборки мусора или (если стек сборки мусора пуст) адреса, содержащиеся в следующем указателе на стек времени выполнения. Затем маркируются все непомеченные ячейки кучи, на которые указывает куча, и их адреса помешаются в стек сборки мусора.
4. Третий шаг повторяется до тех пор, пока освободится стек сборки мусора, и все указатели в стеке времени выполнения будут обработаны описанным образом.
Поскольку на третьем шаге всегда маркируются непомеченные ячейки, то, в конце концов, выполнение алгоритма прекратится.
Описанный выше алгоритм является наглядным, простым для понимания и эффективным. Однако, у него имеется один существенный недостаток – он нереальный, поскольку требует использования стека произвольного размера в момент наибольшей загруженности памяти. Другими словами, сборка мусора просто не будет инициирована. Безусловно, никто не ожидает, что чистка памяти будет выполняться при отсутствии пространства для работы. В то же время, поскольку для сборки мусора требуется небольшой (и известный) объем памяти, то при нехватке памяти ее можно инициировать в первую очередь. Фактически, существует алгоритм сборки мусора с предельно малыми запросами рабочего пространства.
Сборка мусора 2
1. Пометить все ячейки кучи, на которые прямо указывают значения из стека времени выполнения.
2. Просмотреть кучу, начиная с низших адресов, чтобы найти первый помеченный указатель, указывающий на непомеченную ячейку. Пометить эту ячейку.
3. Продолжить просмотр кучи, помечая непомеченные ячейки, на которые указывают помеченные ячейки. Выделить адрес ячейки с наименьшим адресом, помеченным таким способом. Назвать этот адрес низшим.
4. Повторять шаги 2 и 3, уже начиная с низшего адреса, пока при просмотре будет помечаться хотя бы одна ячейка. Поскольку число ячеек, которые необходимо пометить, конечно, то, в конце концов, выполнение алгоритма прекратится.
Помимо пространства, необходимого для битовой карты, алгоритму также требуются три переменные, представляющие:
текущую позицию при просмотре;
ячейку, к которой идет обращение низший адрес, к которому должно идти обращение при текущем просмотре.
В то же время, с точки зрения затрачиваемого времени этот алгоритм может быть крайне неэффективным. В частности, это может быть в том случае, когда в куче содержится много обратных указателей, и это является ценой за неиспользование стека.
Компромиссом между двумя описанными алгоритмами будет алгоритм, придерживающийся стратегии 1 при достаточно свободной памяти к стратегии 2 – в противоположном случае. Например, если стек достаточно большой, то алгоритм может использовать стек фиксированного размера и придерживаться первой стратегии. Как только при увеличении стека станет реальной угроза его переполнения, из стека может удаляться одно значение. Удаленное таким образом нижнее значение стека запоминается и используется для начала второй фазы алгоритма, которая во многом будет подобна сборке мусора 2.
Еще в одном известном алгоритме куча рассматривается как древовидная структура с указателями от вершины к основанию. Сборка мусора начинается с вершины дерева и идет по направлению вниз. Вместо использования стеков для запоминания указателей, требующих последующей обработки, алгоритм использует указатели самого дерева, временно обращая их для обеспечения пути возврата вверх по дереву. Этот алгоритм эффективнее; и с точки зрения времени, и с точки зрения требуемой памяти.
Другие схемы очистки памяти включают различные схемы сборки мусора с учетом поколений (generational garbage collection), в которых производится разделение:
между глобальными объектами, которые существуют относительно долго еще до инициации процесса сборки мусора, и память для которых очищать не обязательно;
локальными объектами, которые существуют меньшее время, и память которых постоянно требуется возвращать в доступную область.
Очевидно, что такая схема уменьшает время сборки мусора и может быть достаточно эффективной. В других схемах для уменьшения времени сжатия кучи используются две глобальные области
Какой бы метод сборки мусора не использовался, может случиться так, что программа просто исчерпает доступную память и будет вынуждена завершить работу, если только система не разрешит эту проблему каким-то иным способом. Память программы может также ограничиваться за счет сборки мусора, если при используемом алгоритме большая часть времени уходит именно на чистку памяти – вскоре после завершения сборки мусора, когда программа уже кажется готовой к продолжению работы, куча снова переполняется, что вновь требует проведения очистки памяти. В такой ситуации служебные издержки на проведение сборки мусора могут быть очень значительными, и именно здесь будет уместным альтернативный подход – использование счетчиков ссылок. Этот метод позволяет (достаточно часто) заменить непредсказуемые издержки на сборку мусора издержками постоянными и предсказуемыми.
При использовании счетчиков ссылок предпринимается попытка очистить каждый элемент памяти кучи сразу же после прекращения обращений к нему. Каждая ячейка памяти в куче имеет счетчик ссылок, в котором фиксируется число значений, обращающихся к данной ячейке. Появление каждой новой переменной, обращающейся к данной ячейке увеличивает значение счетчика, а исчезновение ссылки уменьшает его когда значение счетчика становится нулевым, ячейка может быть возвращена в область свободной памяти для дальнейшего распределения
Этот метод удачен, но имеет некоторые ограничения.
Не может очищаться память, которая связана со структурами данных, подобными кольцевым спискам.
Постоянные издержки, связанные с использованием счетчиков ссылок, могут сильно уменьшать эффективность программ с предельно малыми запросами относительно памяти.
В заключение отметим, что второй пункт противоречит принципу Бауэра, который утверждает, что “простые программы” не должны платить за неиспользование существующих дорогих характеристик языка.