35. Распределение памяти. Дисплей.
Рассмотрим для примера следующую схему программы на языке Pascal.
program demo (output); var x, у: real;
procedure first; var c, d: integer;
procedure second;
var p, q: integer;
begin
..
end;
procedure third;
var m, n: integei
begin
..
end;
begin
second;
third
end;
begin
first;
end.
В момент вызова процедуры second стек времени выполнения может выглядеть подобно изображенному на рисунке.
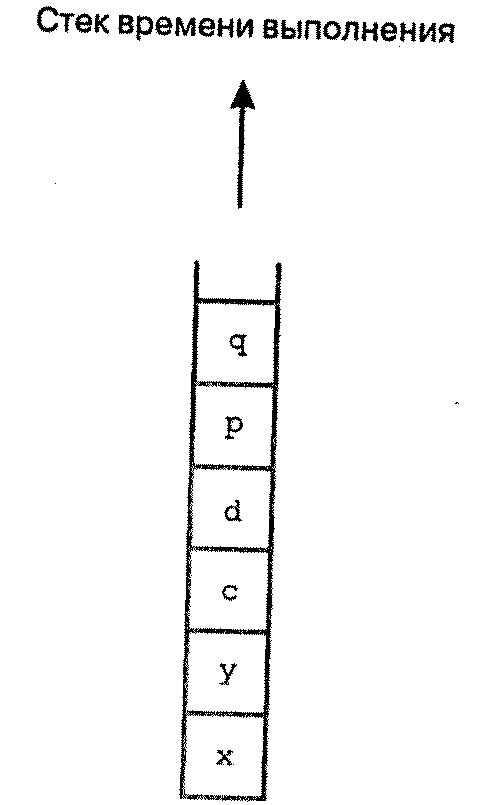
Чтобы облегчить доступ к переменным, объявленным во внешних областях видимости, модель памяти Pascal, возможно, должна будет иметь указатели (называемые статическими указателями) к каждому из доступных в данный момент внешних блоков. Массив таких указателей обычно называют дисплеем.
В то же время он не обязательно соответствует массиву указателей ко всем процедурам, которые сейчас выполняются. Предположим, например, что в процедуре third также имеется обращение к процедуре second. Ситуация непосредственно перед вызовом second из third изображена на рисунке слева, а сразу же после вызова – на рисунке справа.
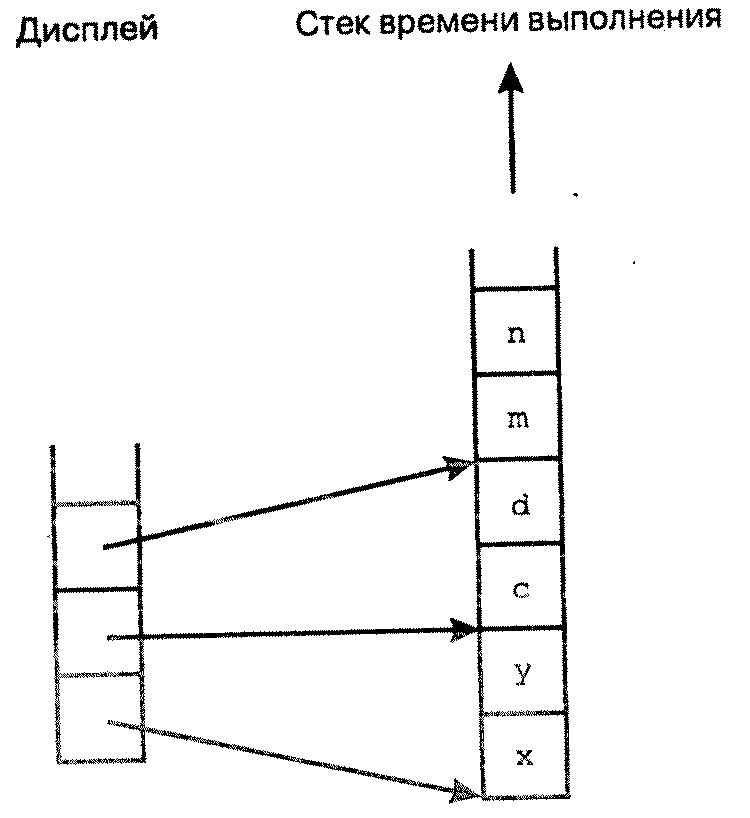
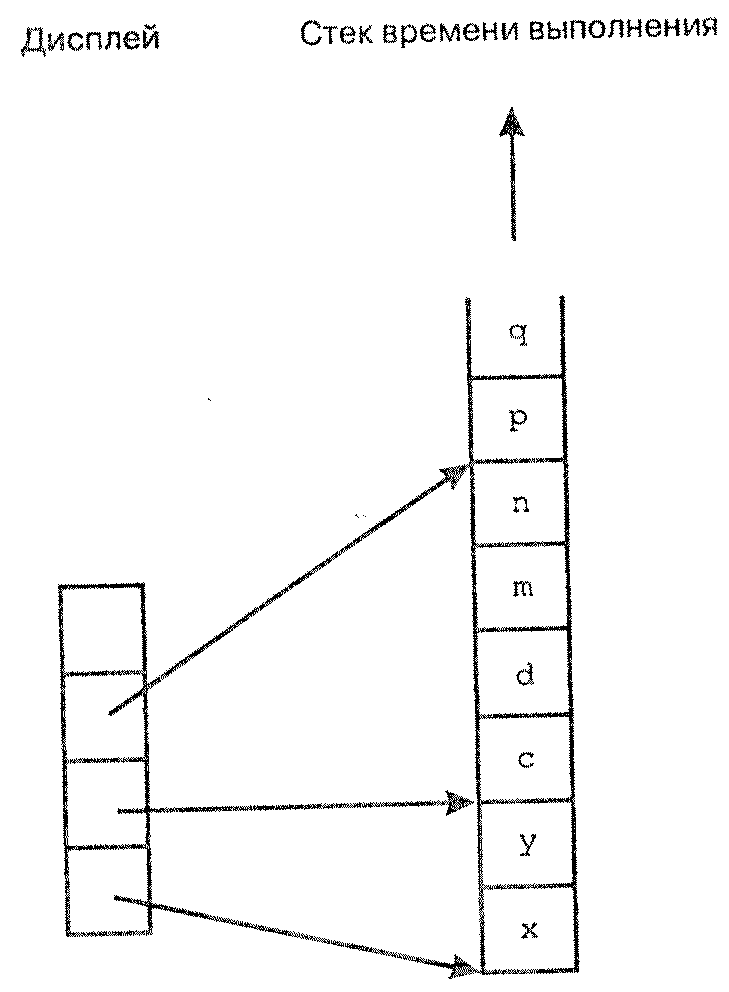
Из иллюстраций видно, что в дисплее содержатся только указатели на блоки с переменными, доступными в данный момент, следовательно, по одному указателю к каждому статическому уровню, к переменным которого возможен доступ. Данная ситуация показана на рисунке справа, где отсутствует возможность доступа к переменным third после вызова second из third. Это связано с тем, что second и third располагаются на одном статическом уровне.
35. Адреса времени компиляции. Простые адреса. Адресация элементов статического массива.
Хотя в процессе компиляции адреса неизвестны, часть информации о них обычно имеется. Например, известны следующие параметры.
Смещение простого значения относительно основания стекового фрейма;
Смещение начала массива относительно основания стекового фрейма;
Статическая глубина функции, в которой объявлена переменная.
Статическая глубина относится к языкам Pascal и Ada (в С такого понятия нет).
В языке С адрес простой переменной в процессе компиляции представляет собой смещение по отношению к основанию стекового фрейма. Это же относится и к полю записи, так как поля записи всегда запоминаются последовательно, и предполагается, что объем требуемой памяти для каждого из полей известен. Для языка Pascal или Ada адрес времени компиляции простой переменной или поля записи будет состоять из пары: (номер уровня, офсет)
Здесь номер уровня – номер статического уровня функции или процедуры, в котором была объявлена переменная или запись, а термин “офсет” употребляется с тем же значением, что и в языке С (смещение от начала фрейма).
Для массивов со статическими границами (значение границ известно в процессе компиляции) адрес элемента массива, в зависимости от применяемого языка, можно также выразить через номер уровня и офсет или просто через офсет. Смещение элемента массива по отношению к основанию стекового фрейма состоит из двух частей.
Смещение начала массива по отношению к основанию стекового фрейма.
Смещение элемента массива по отношению к началу массива.
Для массивов со статическими границами значение первой части известно в процессе компиляции, а второй, в общем случае, – нет, поскольку, в процессе компиляции обычно неизвестно значение индексов массива.
При нахождении адресов элементов массива часть вычислений осуществляется во время выполнения программы с использованием информации, известной при компиляции. Как будет показано далее, объем вычислений зависит от размерности массива. Проиллюстрируем сказанное с помощью следующего примера на языке Pascal.
Рассмотрим объявление массива.var table: array[1..10, 1..20] of integer;
Элементы массива обычно записывают построчно или, точнее, согласно лексикографическому порядку индексов. Например, значения элементов приведенной таблицы будут занесены в память в следующем порядке.
table[1,1], table[1,2],..., table[1,20],
table[2,1], table[2,2],..., table[2,20],
.
table[10,1], table[10,2],..., table[10,20],
Адрес конкретного элемента массива вычисляется как смещение от адреса первого элемента массива.
адрес(table[i,j]) = адрес(table[l1,l2]) + (u2 – l2 + 1)*(i – l1) + (j – l2)
Здесь l1, и u1 – нижняя и верхняя границы первого измерения и т.д., а каждый элемент массива предполагается размером в одну ячейку памяти. В приведенном выше примере нижние границы в каждом случае равны 1, а верхние — 10 и 20 соответственно.
Для трехмерного массива arr3 объявленного как
var аrr3: array [l1…u1, l2…u2, l3…u3] of integer
обшая формула для адреса элемента массива arr3[i,j,k] имеет следующий вид.
адрес(arr3[i,j,k]) = адрес(arr3[l1,l2,l3]) + (u2 – l2 + 1)*(u3 – l3 + 1)*(i – l1) +
(u3 – l3 + 1)*(j – l2) + (k – l3)
Выражение (ur – lr + 1) представляет число различных значений, которые может принимать r-й индекс, т.е. (u3 – l3 + 1) – это число значений, что может принимать третий индекс, а также расстояние между элементами массива, которые отличаются на единицу во втором индексе.
Подобным образом
(u2 – l2 + 1)*(u3 – l3 + 1)
представляет число различных пар значений, которые могут образовать второй и третий индексы, а также расстояние между элементами массива, которые отличаются на единицу в первом индексе. Расстояние между элементами массива, которые отличаются на единицу в i-ом индексе, называют шагом по i-ому индексу (ith stride). Таким образом, в приведенном выше примере шаг по первому индексу равен
(u2 – l2 + 1)*(u3 – l3 + 1)
по второму и третьему – (u3 – l3 + 1) и 1 соответственно
Из приведенной выше формулы для нахождения смещения элемента массива относительно адреса первого элемента массива понятно, что вычисления становятся достаточно простыми, если известны шаги по индексам. Например, для arr3 адрес элемента arr3[i,j,k] выражается следующим образом.
адрес(arr3[i,j,k]) = адрес(arr3[l1,l2,l3]) + s1*(i – l1) + s2*(j – l2) + s3*(k – l3)
Здесь s1, s2, s3 – шаги по соответствующим индексам, равные следующему,
s1 = (u2 – l2 + 1)*(u3 – l3 + 1)
s2 = (u3 – l3 + 1)
s3 = 1
На рисунке показано применение шагов по индексам для нахождения адреса элемента массива из следующего массива, объявленного таким образом (язык Pascal).
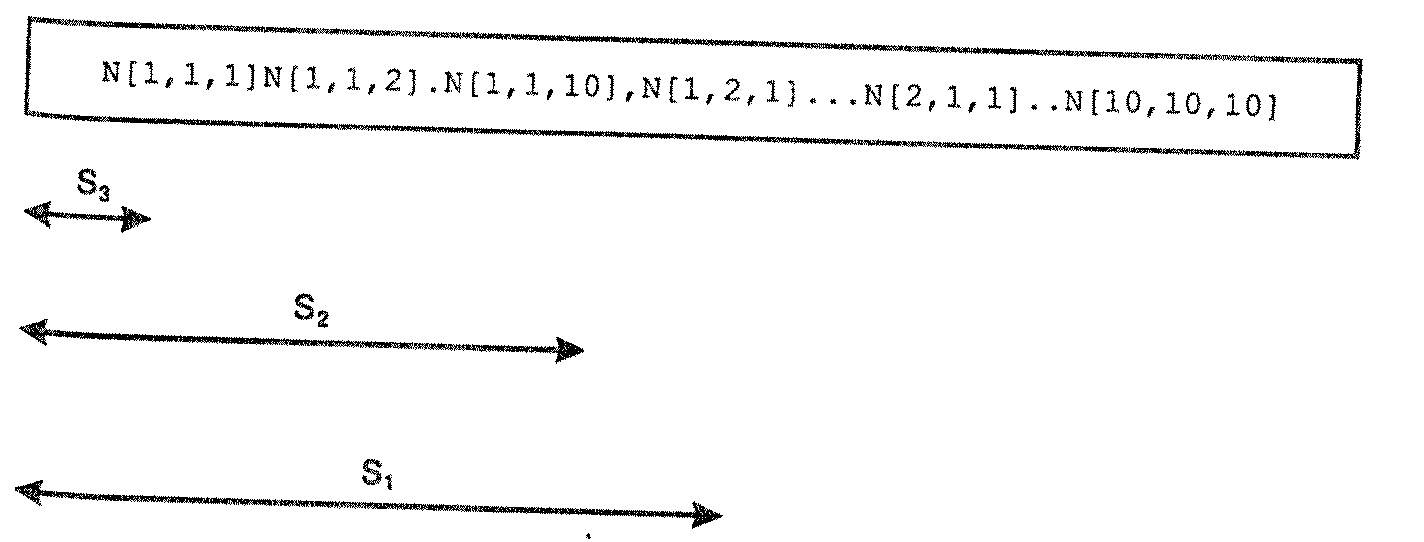
var N: array [1..10, 1..10, 1..10] of integer;
Следовательно, в статической части фрейма будут содержаться следующие значения.
Все простые значения (типы integer, float и т.д.).
Статические части массивов (границы, шаги по индексам, указатели на элементы массива).
Статические части записей (поля, размеры которых известны во время компиляции).
Указатели на глобальные значения – хотя глобальные значения будут храниться не в стеке, а в куче.
Для языков, в которых границы массива известны во время компиляции, значения шагов по индексам могут вычисляться сразу же, что сокращает количество вычислений времени выполнения программы при каждом обращении к массиву. Дальше упростить приведенную формулу уже невозможно, поскольку разность (i – l1), в общем случае, во время компиляции неизвестна.