10. Коэффициент корреляции, его основные свойства, формула для расчета по выборке. Оценка статистической значимости.

Известно, что для независимых величин 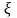и выполняется следующее правило:

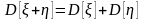.Поэтому, если данное правило не выполняется, то это служит признаком зависимости между и . Это первый критерий стохастической связи двух случайных величин . Для случайных величин доказано .

Итак, зависимость и вытекает из неравенства: .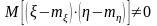

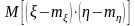называется корреляционным моментом связи. Он зависит от единиц измерения, поэтому на практике используется безразмерная величина – коэффициент корреляции:

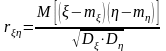1. Выборочный коэффициент корреляции 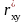вычисляется 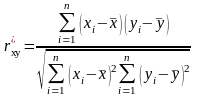. Коэффициент корреляции независимых случайных величин равен нулю; обратное неверно!

2. , где – константы; ;

3. , где – константы любого знака;

4. , где ; ;

5. ;

6. ;

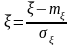При 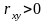связь прямая, при – обратная. Если , то связь считается слабой. При 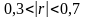связь считается средней, а при – сильной.

Если 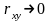, то это не означает, что связь обязательно отсутствует, она может быть сильно нелинейной.Как оценить точность приближения к (истинному коэффициенту корреляции).Ответить на этот вопрос позволяет знание закона распределения вероятностей. Используется 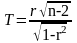– двусторонний t критерий Стьюдента, который имеет распределение Стьюдента с 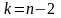и уровнем значимости . Если 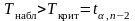, то нулевая гипотеза об отсутствии корреляционной связи между х и у отторгается с вероятностью ошибки, равной .

11. Модель парной регрессии. Задачи построения уравнения регрессии. Модель линейной регрессии.

12. Метод наименьших квадратов

13. Условия Гаусса-Маркова. Классическая линейная регрессивная модель. Показатели качества уравнения регрессии. Прогноз по уравнению регрессии.

Насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей генеральной совокупности. 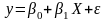(1)

Уравнение 1 – теоретическое уравнение регрессии. (2)

Уравнение 2 – эмпирическое уравнение регрессии.

Для того, чтобы регрессионный анализ, основанный на обычном МНК, давал наилучшие из всех возможных результаты, случайное отклонение 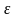должно удовлетворять условиям Гаусса-Маркова:

1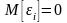 для всех наблюдений. Это означает, что в среднем случайное отклонение не оказывает влияния на зависимую переменную. А также не должно быть систематического смещения.

2Дисперсия случайных отклонений для всех наблюдений постоянна 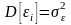. Величина конечно неизвестна. Если рассматриваемое условие не выполняется, то обычный МНК не эффективен.

3Случайные отклонения и для 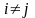являются некоррелированными: – отсутствие систематической связи между значениями случайного отклонения в любых двух наблюдениях.

При выполнении условий 1-3 уравнение 1 называется классической линейной регрессионной моделью.

Насколько широко рассеяны точки наблюдений относительно линии регрессии. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. Мерой качества уравнения регрессии, характеристикой прогностической силы регрессионной модели является коэффициент детерминации, определяемый по формуле ,где ; ; – общая сумма квадратов отклонений зависимой величины от ее среднего. показывает, какая доля вариации зависимой переменной обусловлена вариацией объясняющей переменной. в случае парной линейной регрессии (доказывается).

Также проверка общего качества уравнения регрессии осуществляется по критерию Фишера - эмпирическое уравнение регрессии значимо на уровне , если 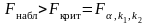,где , .