6. Уравнения математической физики. Уравнение колебаний струны, формулировка краевой задачи.

В математической физике под струной понимают гибкую упругую нить. Пусть струна длиной е в начальный момент направлена по отрезку оси 0Х и Х=l. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе, то струна будет колебаться, точки струны будут совершать движения. Задача заключается в определении формы струны в момент времени и определении закона движения каждой точки струны от времени.

Будем рассматривать малые отклонения точек струны от начального положения. Отклонение в момент t в точке Х малое. Т.к. мы рассматриваем малые отклонения струны в плоскости (Х, U), то будем предполагать, что длина элемента струны (проекции). Также предположим, что натяжение во всех точках струны одинаковые, обозначим его Т.

Рассмотрим элемент струны . На концах этого элемента по касательным к струне действуют силы Т. Пусть касательные образуют c осью 0Х углы φ и φ+φΔ. Тогда проекция на ось 0U сил, действующих на элемент , будет равна

.

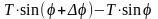Поскольку угол φ мал (отклонение малое), то можно положить и тогда

, при .

Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. – линейная плотность струны. Тогда масса элемента струны будет . Ускорение элемента равно , следовательно .

Сокращая на и обозначая , получим уравнение движения (1)

Уравнение (1) – и есть уравнение, уравнение колебаний струны. Но для определения движения струны уравнения (1) недостаточно. Искомая функция должна удовлетворять еще граничным условиям, указывающим что делается на концах струны, и начальным условиям, описывающим состояние струны в начальный момент . Совокупность граничных и начальных условий называется краевыми условиями.

Например, концы струны неподвижны, тогда

, . (2)

Равенства (2) являются граничными условиями в нашей задаче. В начальный момент струна имеет форму , которую мы ей придали, т.е.

. (3)

Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется :

. (4)

Задача (1)-(2)-(3) и есть краевая задача для отыскания колебаний струны.

7. Уравнение распространения тепла в стержне, вывод. Формулировка краевой задачи.

Рассмотрим однородный стержень длины (рисунок 1). Боковая поверхность стержня теплонепроницаема и во всех точках поперечного сечения стержня температура одинакова.

Рисунок 1 – Однородный стержень

Изучим распространение тепла в стержне. Расположим ось 0Х как на рисунке. - температура в сечении стержня с абсциссой Х в момент времени t. Установлено, что скорость распространения тепла, т.е. количества тепла, протекающего через сечение с абсциссой Х за единицу времени, определяется как

, (1)

где – коэффициент теплопроводности, – площадь сечения.

Формула (1) следует из закона удельного теплового потока Фурье:

.

Рассмотрим элемент стержня, заключенный между Х₁ и Х₂; . Количество тепла, прошедшее через сечение Х₁ за время будет

.Аналогично для сечения Х₂: .

Тогда поток тепла в элемент стержня за время будет равен

(2)

.

Этот приток тепла за время затратился на повышение температуры элемента стержня на величину

, (3)

где – масса элемента стержня, с – теплоемкость.

Приравнивая (2) и (3), получим

,

Разделим полученное выражение на :

; ; .Обозначая 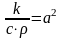(коэффициент температуропроводности) окончательно получим уравнение теплопроводности (4): . (4)

Чтобы решение уравнения (4) в однородном стержне было определено, функция должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Эти условия могут быть разные.

Первая краевая задача:

, (5)

, (6)

, (7)

где (5) – начальное условие; (6), (7) – граничные условия.

Условие (5) означает, что в начальный момент времени в различных сечениях стержня задано распределение температур . Условия (6), (7) соответствуют тому, что на концах стержня поддерживается температура и соответственно. Доказано, что уравнение (4) имеет единственное решение в области ; , удовлетворяющее условиям (5)-(7).