
- •Глава 2. Теория пределов
- •§1. Понятие предела функции
- •§2.Односторонние пределы
- •§3. Случаи стремления к 0, .
- •Свойства бесконечно малых и бесконечно больших функций:
- •Бесконечно – малые функции, эквивалентность функций при
- •§4. Основные свойства пределов (теоремы о пределах)
- •§5. Замечательные пределы
- •§6. Техника вычисления различных пределов
- •§7.Непрерывность функции
- •Точки разрыва и их классификация
§5. Замечательные пределы
В теории пределов большую роль играют два предела, которые, в силу их важности, получили названия замечательных пределов.
Теорема.
Функция
|
|
данный предел называется первым замечательным пределом.
Доказательство:
Рассмотрим единичную окружность на рис. 44.
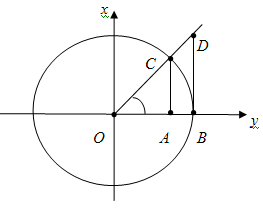
Рис. 44.
Пусть
, ∠COB
=
x,
 ,
OC
=
OB =
r
=
1,
AC=sinх,
OA=cosx,
BD=tg
x.
Сравнивая
площади
треугольника
OAC,
сектора
OBC
и
треугольника
OBD,
получаем
,
OC
=
OB =
r
=
1,
AC=sinх,
OA=cosx,
BD=tg
x.
Сравнивая
площади
треугольника
OAC,
сектора
OBC
и
треугольника
OBD,
получаем
 ,
,
 .
.
Разделим
двойное неравенство на
 >0:
>0:
 .
(1)
.
(1)
Неравенство
(1) справедливо для x<0,
так как
 ,
,
 .
Перейдем к пределу при x→0:
.
Перейдем к пределу при x→0:
 -
функция непрерывная, cosx→
cos(0) =1. В неравенстве (1), переходя к
пределу, получаем:
-
функция непрерывная, cosx→
cos(0) =1. В неравенстве (1), переходя к
пределу, получаем:
 ,
т.е.
.
,
т.е.
.
!
В
первом замечательном пределе имеет
место неопределенность
 .
.
Следствие из теоремы:
1.
![]() ;
4.
;
4.
 ;
;
2.
![]() ;
5.
;
5.
 ,
где
,
где
 -
число.
-
число.
3.
![]() ;
;
Пример
2. Вычислить
предел .
.
Решение.
Если x→0,
то и
 ,
тогда
,
тогда
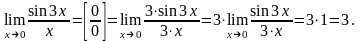
Теорема.
Функция ,
, при
при имеет
предел:
имеет
предел:
 ,
где
,
где
![]() .
Более точно
.
Более точно
![]() ,
т.е. число
,
т.е. число
![]() – иррациональное число. Данный предел
называется вторым
замечательным пределом.
– иррациональное число. Данный предел
называется вторым
замечательным пределом.
В
результате замены переменной
 получается
еще одна форма записи второго замечательного
предела:
получается
еще одна форма записи второго замечательного
предела:
|
|
|
|
Следствие из теоремы:
1.  ;
2.
;
2.  .
.
Пример
3. Вычислить
предел .
.
Решение.
Представим функцию
![]() в виде
в виде
![]() .
Тогда функция
.
Тогда функция
![]() эквивалентна функции
эквивалентна функции
![]() при
.
Следовательно,
при
.
Следовательно,
 .
.
§6. Техника вычисления различных пределов
Рассмотрим несколько основных приёмов, применяемых при вычислении пределов последовательностей и функций:
Прием №1. Если функция элементарная и предельное значение аргумента принадлежит ее ОДЗ, то вычисление предела сводится к вычислению значения функции;
Пример
4.
Вычислить
предел
 .
.
Решение.
Так как
![]() ,
то числитель дроби стремится к числу
,
то числитель дроби стремится к числу
![]() ,
а знаменатель – к числу
,
а знаменатель – к числу
![]() .
Следовательно
=
.
Следовательно
=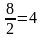 .
.
Прием №2. Если функция дробно-рациональная, при неопределенности типа нужно числитель и знаменатель дроби делить на высшую степень х и применить свойство бесконечно большой функции ;
Пример
5. Вычислить
предел
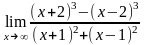 .
.
Решение.
Упростим числитель и знаменатель,
используя формулы сокращенного умножения:

 .
.
Числитель и знаменатель дроби при неограниченно возрастают. В
этом случае говорят, что имеет место неопределенность вида . Разделив
на
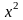 числитель и знаменатель дроби, получаем
числитель и знаменатель дроби, получаем
 .
.
Из свойств пределов и свойств бесконечно малых функций следует, что
 .
.
Прием №3. Если функция дробно-рациональная, при неопределенности типа следует числитель и знаменатель дроби разложить на множители и сократить;
Пример
6. Вычислить
предел
 .
.
Решение.
Числитель и знаменатель дроби при
![]() стремятся к нулю (неопределенность вида
).
Разложив числитель и знаменатель на
множители, получим
стремятся к нулю (неопределенность вида
).
Разложив числитель и знаменатель на
множители, получим
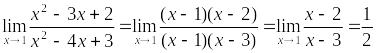
Прием №4. Для преобразования радикалов(корней) в дробном выражении, используя основное свойство дроби следует умножить на сопряженные множители;
Пример
7.
Вычислить предел
 .
.
Решение.
Числитель и знаменатель дроби при
стремятся к нулю. Для того чтобы избавиться
от неопределенности
,
умножим числитель и знаменатель дроби
на выражение
![]() .
Тогда, используя формулу сокращенного
умножения, получим
.
Тогда, используя формулу сокращенного
умножения, получим
|
|
|
|
Прием №5. Предел от тригонометрических функций, неопределенности типа могут раскрываться при помощи первого замечательного предела и его следствий;
Пример
8. Вычислить
предел
 .
.
Решение. Используем теорему о первом замечательном пределе и следствие из нее:
|
|
Прием №6. Неопределенность типа могут раскрывать при помощи второго замечательного предела и его следствий;
Пример
9. Вычислить
предел
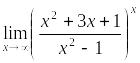 .
.
Решение. Делением числителя дроби на знаменатель выделим целую часть:
|
|
Таким
образом, при
![]() данная функция представляет собой
степень, основание которой стремится
к единице, а показатель – к бесконечности
(неопределенность вида
данная функция представляет собой
степень, основание которой стремится
к единице, а показатель – к бесконечности
(неопределенность вида
![]() ).
Преобразуя функцию так, чтобы использовать
второй замечательный предел, получим
).
Преобразуя функцию так, чтобы использовать
второй замечательный предел, получим
|
|
|
|
Так
как
 является
бесконечно малой функцией при
,
является
бесконечно малой функцией при
,
|
|
Учитывая,
что
! Вспомогательные формулы:
|
|
Прием
№7.
При
вычислении пределов вида
 возникают
неопределенности вида
,
,
можно воспользоваться формулой:
возникают
неопределенности вида
,
,
можно воспользоваться формулой:
 .
(2)
.
(2)
Пример
10. Вычислить
предел
 .
.
Решение.
Применяя формулу (2), получаем
 .
.
Прием №8. В случае неопределенностей или необходимо выражение сделать дробным и привести к неопределенностям типа , , далее применить известный прием.

 при
при
 ,
,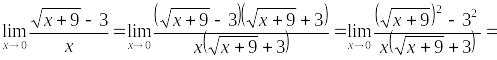
 .
.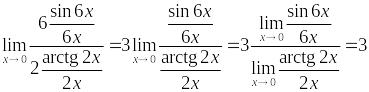 .
.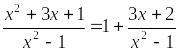 .
.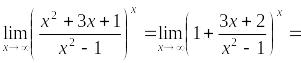
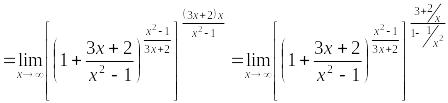 .
.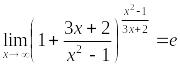 .
.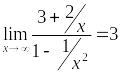 ,
находим
,
находим
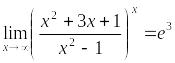 .
.


 .
.