Глава 2. Теория пределов

Определение предела впервые появилось в XVII пеке. Зачатки теории пределов можно обнаружить, например, и работах английского физика и математика Исаака Ньютона (1642—1727). Однако математики XVII и XVIII веков не ставили своей задачей построить стройную теорию пределов. Эта задача была поставлена и решена лишь в XIX веке. Большая заслуга в этом принадлежит французскому математику Коши (1789—1857). Он развил теорию пределов и положил ее в основу построения одного из важнейших разделов математики — математического  анализа. Символ предела появился в 1787 году у швейцарский математика Симона Люилье, хотя предельное значение аргумента сначала указывался отдельно, после символа lim. Близкое к современному обозначение ввёл Вейерштрасс, однако вместо привычной нам стрелки он использовал знак равенства. Стрелка появилась в начале XX века сразу у нескольких математиков — например, у Харди (1908).

Вычисление пределов последовательностей и функций  классическая задача математического анализа. Без вычисления пределов не обойтись при исследовании и построении графиков функций, вычислении определенных и несобственных интегралов, исследовании сходимости числовых и функциональных рядов.

§1. Понятие предела функции

Для того чтобы определить предел функции, необходимо ввести понятие предела на последовательном числовом множестве.

► Бесконечной число­вой последовательностью (или просто числовой последовательно­стью) называется функция a_n = f(n), определенная на множестве всех натуральных чисел 1, 2, ..., п, ... . Значения последователь­ности а₁, а₂, …, a_n, … называются ее членами.

Последовательность a_n = f(n) иногда обозначают так: {а_п}. Это означает, что задана последовательность с общим членом а_n. По данному общему члену всегда можно найти любой член по­следовательности a_k подставив в а_n вместо п число k. Ниже при­ведены примеры последовательностей, причем сначала приведе­на форма записи {a_n}, а затем записаны первые члены: {(-1)ⁿ n}; -1, 2, -3, …;

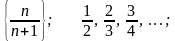
{Зn + 1}; 4, 7, 10, ...;

Величины, рассматриваемые в математике, бывают постоянными и переменными. Под переменной величиной понимают величину, которая может принимать различные числовые значения при заданном исследовании, в том числе и значения бесконечной числовой последовательности. Переменные принято обозначать латинскими буквами, например неизвестные в уравнениях обозначаются .

Графическим изображением множества последовательных значений переменной величины может быть прямая, луч, интервал или отрезок.

Рассмотрим процесс, состоящий в том, что переменная величина х, неограниченно приближается к величине а и пробегает последовательно множество значений. Различные переменные величины к своему предельному значению могут стремиться по разному: убывая справа, возрастая слева, колеблясь около своего предельного значения, и при этом ни одно значение х не является последним (см. рис.38).

Рис.38.

Тогда говорят, что х стремится к пределу а, или записывается .

Обозначается предел в математике 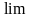, cледовательно, вышесказанное можно записать .

► Окрестностью точки называется любой интервал ,

содержащий данную точку: . В частности, 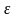- окрестностью

точки называется интервал (см. рис.39).

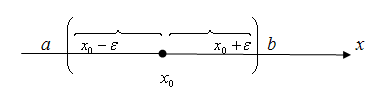
Рис. 39.

Рассмотрим функцию , которая определена в некоторой окрестности а, за исключением, быть может, самой точки а.

► Число А называется пределом функции в точке , если при

любом значении , соответствующее значение функции у стремится

к А, .

Обозначается предел функции .

Пример 1. Выражение и функциональная зависимость при не имеет смысла, но в теории пределов можно записать . На графике (см. рис. 40) видно, что в окрестности точки 0, график бесконечно приближается, но не существует.

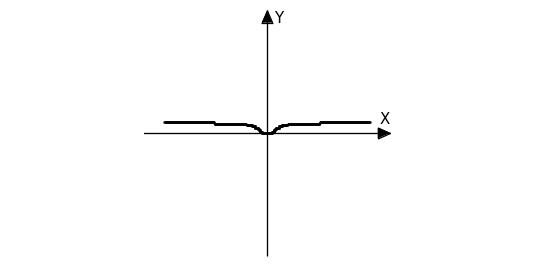
Рис. 40.

В математическом анализе существует много определений предела. Для строгих доказательств теорем ученые пользуются следующим:

Основное классическое определение предела функции (сформулировано «на языке эпсилон-дельта» или «на языке окрестностей», иначе определение предела по Коши).

► Число А называется пределом функции при стремящимся к а,

если для любого малого существует такое малое 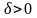, что

неравенство выполняется, как только выполняется .

! Смысл этого определения заключается в том, что чем ближе точка x расположена к точке a , тем ближе значение f(x )к числу A.

Студенты – математики записывают определение предела функции коротко, используя символы мат.анализа:

Геометрический смысл предела функции показан на рисунке (см. рис.41). Точки графика функции с абсциссами из окрестности точки a и соответствующими им ординатами из окрестности точки A должны лежать в полосе, ограниченной двумя прямыми y=A+ и y=A- .

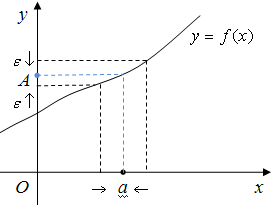
Рис.41.