4. Статистический анализ регрессионной модели статики

Получив математическое выражение выбранной структуры модели, далее производится анализ этой модели на основе статики.

Выделяются 3 направления статистического анализа:

1. Регрессионный;

2. Корреляционный;

3. Дисперсионный.

4.1. Регрессионный анализ

Регрессионный анализ включает в себя много этапов (процедур проверки), главными из которых являются:

1. Оценка значимости коэффициентов полученной модели;

2. Оценка адекватности модели данного эксперимента.

4.1.1.Оценка значимости коэффициентов полученной модели

Все численные значения коэффициентов модели случайные величины . Установлено, что они имеют нормальный закон распределения.

,

где – генеральное математическое ожидание,

– генеральная дисперсия.

Для каждого из коэффициентов модели необходимо выяснить равно ли нулю генеральное математическое ожидание, если , такие коэффициенты называются незначимыми. В рассматриваемой модели они случайно отличаются от нуля. Незначимые коэффициенты необходимо убрать из модели и модель пересчитать снова без них.

Для каждого коэффициента полной и выборочной модели формируется нулевая гипотеза.

.

, т.е. или .

Задается уровень ошибки первого рода .

Для проверки гипотезы применяется статистика Стьюдента (t-статистика)

,

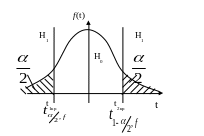
- число степеней свободы.

Т.к. всегда, то попасть в левую полуплоскость невозможно. Поэтому сравнивается только со 2-ой границей.

Если , то «нулевая гипотеза» отвергается с вероятностью ошибки 5%. Значит у данного коэффициента генеральное математическое ожидание , т.е. коэффициент значим.

Если , то принимается «нулевая гипотеза» с вероятностью ошибки 5%. Коэффициент не значим, его нужно убрать из модели.

По таблице Стьюдента:

Для полной модели t_кр1 = 2,11

Для выборочной модели t_кр2 = 2,10

По полученным данным лабораторной работы уже имеется t-статистика для каждого из коэффициентов, поэтому сравниваются уже имеющиеся данные.

А) Оценка значимости коэффициентов (полная модель):

Y1 =11.75+2.367*X1+-0.7588*X2+0.7332*X1X1+1.059*X2X2+

-1.471*10^-3*X1X2

H₀: B_j=0;

H₁: B_j≠0;

;

№	КОЭФ МОДЕЛИ bi	ОШИБ КОЭФ	Т - СТАТИСТИКА	ОЦЕНКА ЗНАЧИМОСТИ
1	11.75	0.7821	15.02	значим
2	2.367	0.7622	3.105	Значим
3	-0.7588	0.6088	1.246	незначим
4	0,7332	0.5679	1.291	незначим
5	1.059	0.5287	2.003	незначим
6	-1.471	0.6199	2.373*10-3	незначим

t_расч>t_кр для b1,b2 значит справедлива альтернативная гипотеза и данные коэффициенты значимы. Пренебрегать ими нельзя. Коэффициенты b3, b4, b5, b6- незначимы. Решение принимается с вероятностью ошибки равной .

Б) Оценка значимости коэффициентов (выборочная модель):

Y1 = 12.03 + 2.064*X1 + -0.4353*X2 + 1.165*X1X1 + -1.502*10^-4 *X1X2

H₀: B_j=0;

H₁: B_j≠0;

;

№	КОЭФ МОДЕЛИ bi	ОШИБ КОЭФ	Т - СТАТИСТИКА	ОЦЕНКА ЗНАЧИМОСТИ
1	12.03	0.6019	19.99	значим
2	2.064	0.5821	3.546	значим
3	-0.4353	0.4652	0.9358	незначим
4	1.165	0.4373	2.663	значим
5	-1.502*10-4	0.4015	3.741*10-4	незначим

t_расч<t_кр для коэффициентов b3,b5, значит по результатам опыта они случайно отличаются от нуля, поэтому являются незначимыми. Эти коэффициенты нужно убрать из модели. Остальные коэффициенты(b2, b1, b4) – значимы.

Решение принимается с вероятностью ошибки равной .