5. Изгиб. Построение эпюр поперечных сил и изгибающих моментов.

Для балки с заданными сосредоточенными нагрузками построить по характерным точкам эпюры поперечных сил и изгибающих моментов.

Р ешение:

1. Разделяем балку на участки по характерным точкам.

2. Определяем поперечные силы в характерных точках и строим эпюру поперечных

Q = ±∑F_IY

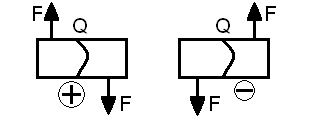
. Q =

Q =

Q =

Q =

Рисунок -Схема нагружения балки с Q =

эпюрами Q и Миз

3. Определяем изгибающие моменты в характерных точках и строим эпюры моментов Миз=±∑Мс(F)

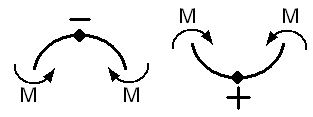
M =

M =

M =

M =

M =

6. .Изгиб. Выбор рациональной формы поперечного сечения балки.

Для стальной двух опорной балки определить опорные реакции, построить эпюру изгибающих моментов и подобрать размеры поперечного сечения следующих вариантов: двутавр, сдвоенный швеллер, круг, прямоугольник. Сравнить массы балок каждых сечений, выбрать рациональное сечение, если [σ] = 160 МПа, h/b=2.

Решение

1. Рассмотрим равновесие балки

2. Освободим балку от связей, действие связей реакциями.

3. Найдем реакции опор, используя уравнения равновесия для произвольной плоской системы сил

Рисунок 21- Заданная схема конструкции балки

с эпюрой изгибающих моментов

ΣM_A(F) = 0 |

ΣM_B(F) = 0 |

R_B =

R_AY =

Поверка:

ΣF_IY = 0 |

0 = 0, значит вычисления выполнены верно.

4. Построим эпюру изгибающих моментов.

М_ИЗГ = ΣМ_С(F)

M =

M =

M =

M =

M =

Опасным является сечение в точке где возникает максимальный изгибающий момент.

5. Вычисляем осевой момент сопротивлений.

σ_ИЗГ = М_ИЗГ/W_Z ≤ [σ]; W_Z ≥ М_ИЗГ/[σ]

W_Z ≥ ≥

6. Подбираем сечение балки в виде:

а) двутавра

№ W_Z = A =

б) сдвоенного швеллера

W_Z = W_Z(2шт)/2 = =

№ W_Z = A =

в) круга

W_Z = πd²/32

A = πd²/4

A =

г)прямоугольника

h/b = 2 (по условию)

W_Z = 2/3∙b³

Вывод. Наиболее экономичными является такие формы поперечных сечений, которые имеют наименьшую площадь. Так как затраты материала при одинаковой длине балок пропорциональны площадям их поперечных сечений, то наиболее экономичным является сечение двутавр.