3. Срез, смятие. Расчет шарнирного узла а.

Рычаг, прикрепленный к опоре А удерживается в равновесии стержнем BD, Соединение в точках А, В и D шарнирное. Рычаг нагружен силой F=3 kH. Определить диаметр оси шарнира узла А из условия прочности на срез и проверить соединение на смятие, если a = 45 мм, b = 225 мм, α = 20°, [σ_см] = 140 МПа, [τ_ср] = 80 МПа.

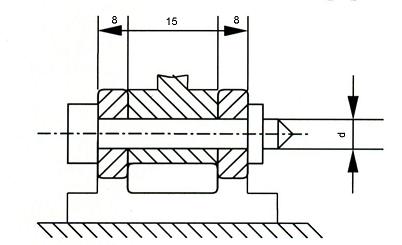
Рисунок - Заданная схема конструкции рычага Рисунок -Конструкция узла А

Решение:

1. Рассмотрим равновесие рычага.

2. Освободим рычаг от связей, действие связей заменим реакциями.

3. Составим уравнения равновесия для полученной произвольной плоской системы сил, и определим реакцию опоры А.

Р исунок - рычаг освобожденный от связей

ΣF_IX = 0

ΣF_IY = 0

ΣM_A(F) = 0

Имеем систему 3-х уравнений с тремя неизвестными, то есть задача статически определяема.

R_AX= R_AY= R_A=

4. Поперечная сила для оси шарнира численно равна реакции опоры А. |Q|=|R_A|=

5. Используя условие прочности на срез, определим диаметр оси шарнира

τ_ср = Q/n* Aср ≤ [τ_ср] Аср= πd²/4 n=2

6. Определяем фактическое напряжение смятия и сравниваем его с допускаемым.

σ_см = R_A/A_CM ≤ [σ_см] Acм=d* =15 мм (По чертежу)

σ_см = R_A/d∙ =

Получается, что рабочее напряжение σ_{см =} ≤ [σ_см] = 140 мПа меньше, значит, условие прочности соблюдается. Соединение работает с недогрузкой (перегрузкой).

4. Кручение, расчет вала.

Для стального трансмиссионного вала определить внешние вращающие моменты на ведущем и ведомом шкивах. Построить эпюру крутящих моментов для двух вариантов расположения шкивов. Первый вариант расположения шкивов принять согласно схеме задания. Второй вариант выбрать самостоятельно. Для рациональной схемы расположения шкивов, из условия прочности и жесткости определить диаметр вала, если выполнить его сплошным, и найти размеры кольца, если вал сделать полым. Диаметр вала считать по всей длине постоянным. Окончательное принимаемое значение диаметра вала округлить до ближайшего четного или оканчивающегося на 5 числа мм. Для вала кольцевого поперечного сечения принять отношение диаметров d_вн/d_нар = 0,65. Сравнить массу сплошного и полого вала, если известно:

P₂= кВт, P₃= кВт, P₄= кВт, n = об/мин, [τ_кр] = Н/мм²,

[φ_отн] = град/м, G =8·10⁴МПа

Рисунок - Заданная схема конструкции вала

Решение

1. Определить угловую скорость вала:

ω = π·n/30 = 3.14· = рад/с;

2. Мощность, передаваемая первым валом:

P₁ = P₂ + P₃ + P₄ = = кВ

3. Определим внешние вращающие моменты:

T = P/ω;

T₁ = P₁/ω₁ =

T₂ = P₂/ω₂ =

T₃ = P₃/ω₃ =

T₄ = P₄/ω₄ =

Проверка ΣT_ix = 0; T₁ + T₂ + T₃ + T₄ = 0;

0=0 => вращающие моменты найдены верно

4. Определяем крутящие моменты по участкам и строим эпюру моментов:

M_кр = ΣM_x(F);

M_кр1 = 0;

M_кр2 =

M_кр3 =

M_кр4 =

M_кр5 =

M_кр.мах =

Рисунок - Заданная схема конструкции Рисунок - Заданная схема конструкции

с эпюрой крутящих моментов с эпюрой крутящих моментов

(1 вариант расположение шкивов) (2 вариант расположение шкивов)

5 . Поменяем местами 1 и 2 шкивы, построим эпюру крутящих моментов:

M_кр1 = 0;

M_кр2 =

M_кр3 =

M_кр4 =

M_кр5 =

M_кр.мах =

Рациональной является схема расположения шкивов, так как max момент равный , имеет большее значение.

6. Определяем диаметр вала для рациональной схемы расположения шкивов при M_кр.мах =

Сечение вала – круг:

Из условия прочности:

τ = V_кр/W_p ≤ [τ_кр]

W_p ≥ Mкр/[τ_кр] Wp=π·d³/16

Условие жесткости:

Φ₀ = 180·M_кр / π·G·I_p ≤ [φ_отн]

I_p ≥ 180· M_кр / π·G [φ_отн] I_p = π·d⁴/32

G=8*10⁴мПа (по условию) Принимаем окончательно d=

Сечение вала – кольцо:

Из условия прочности:

W_p ≥ Mкр/[τ_кр] _{с=dвн/dнар=0.65 (по условию)}

Из условие жесткости:

Принимаем окончательно dнар= dвн=0.65*dнар=

7. Определяем отношение масс валов с сечением круг и кольцо. Поскольку масса балки пропорциональна, площади ее поперечного сечения, то отношение масс валов одинаковой длины равно отношению площадей их сечений.

Площадь круглого сечения: A_кр = π∙d²/4 =

Площадь кольцевого сечения: A_к = π∙(dн²- dвн²)/4=

Отношение масс: A_кр/A_к =

Следовательно, вал кругового сечения в раз тяжелей кольцевого сечения.