2

2. Расчетно-графическая работа по сопротивлению материалов.

3. 0. 2.1. Растяжение, сжатие. Расчет бруса.

Для стального бруса, нагруженного силами F1, F2, F3, построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса в опасном сечении, вычислить перемещение свободного конца, при |σ| = 160 МПа и

E = 2·10⁵ МПа

. РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ.

2.1 Растяжение, сжатие. Расчет бруса

Для заданного бруса, нагруженного продольными силами построить эпюры продольных сил и нормальных напряжений, проверить его прочность, и определить перемещение свободного конца бруса, приняв при этом допускаемое напряжение [σ]=160 Мп, коэффициент пропорциональности Е = 2*10 Мп

Решение

1. Разбиваем брус на участки.

2. Используя метод сечений, определяем продольные силы по участкам, строим эпюру продольных сил.

N=±ΣF_ix

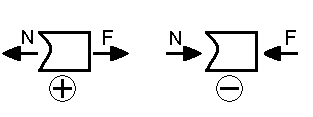
N_I=

N_II=

N_III=

Рисунок - Схема конструкций бруса

с эпюрами N и напряжений .

2. Определяем нормальное напряжение по длине бруса и строим эпюру напряжений σ=N/A

σ₁=N_I/A₁=

σ₂=N_II/A₂=

σ₃=N_III/A₂=

Опасным является участок, где| σ_мах| =

4. Производим проверку прочности бруса в опасном сечении σ_мах≤[σ]

Процент недогрузки (перегрузки):

δ=|(σ – [σ]) |*100% /[σ] =

Для уменьшения процента недогрузки необходимо изменить площадь поперечного сечения. Пересчитаем площадь в опасном сечении при заданных нагрузках. Примем условно, что σ в опасном сечении получилось 160 МПа

A = N/|σ| =

5. Определяем перемещение свободного конца бруса.

Δl_полн. = ΣΔli;

Δl_полн. = Σσ₁·l₁/E =

– брус укорачивается (удлиняется)

2. .Растяжение, сжатие. Определение размеров поперечного сечения балки.

Балка АВ нагружена, как показано на рисунке. Определить диаметр сечения стержня ВС из условия прочности, если известны: σ_r = 240 МПа, [n] = 1.5, F = 25кН, q = 6.4кН/м, α = 60˚. Какого номера необходимо взять прокат, если стержень изготовить из равнополочного уголка?

Рисунок 13- Заданная схема конструкции балки Рисунок 14- Балка, освобождённая от связей

Решение:

1. Рассмотрим равновесие балки АВ.

2. Освободим балку АВ от связей, действие связи заменим реакциями. Равномерно-распределенную нагрузку интенсивностью q заменим сосредоточенной силой Q, приложенной в центре участка действия нагрузки.

3. Используя условия равновесия для произвольной системы сил, определим реакцию стержня ВС

ΣМ_А(F)=0

4. Под действием силы R_BD= стержень работает на растяжение и продольная сила равна

|N_BD| = |R_BD| =

5. Определяем допустимое напряжение при растяжении:

σ = σ_пр / [n] = σ_max /[n]; σ=

6. Используя условия прочности при растяжении, определим требуемую площадь поперечного сечения стержня BD.

σ = N_BD / A ≤ [σ]; A ≥ N_BD/[σ]; A ≥

7. Определим требуемый диаметр стержня BD.

A = π·d²/4; _{; d} ≥ _{Принимаем d=}

8. По таблицам сортамента прокатной стали определим номер равнополочного уголка по требуемой площади A ≥ Атабл= №