Устройство червячной тали

Ручные червячные тали (рисунок 6.1) подвешиваются к потолочным балкам, треногам или другим устройствам с помощью крюка 5. Грузоподъемность ручных талей 0,5–5 т, высота подъема до 3 м. Тяговым органом в ручных талях является грузовая пластинчатая или овально-звеньевая цепь 1, охватывающая звездочку 3, жестко связанную с червячным колесом 4. Для увеличения КПД червячного зацепления и скорости подъема груза применяют червячную двухзаходную передачу, не являющуюся самотормозящей, поэтому на валу червяка 7 устанавливают дисковый или конический грузоопорный тормоз 2 с неразмыкающимися поверхностями трения. Вращение червяка осуществляется цепным колесом 6 с помощью тяговой сварной цепи 8. Для захвата груза служит крюковая подвеска 9, которая связана с грузовой цепью 1, концы которой закреплены к тали таким образом, чтобы образовать полиспаст, кратность і_n = 2.

Работа червячной тали

Работу тали рассмотрим для трех периодов: период подъема груза; период, когда груз подвешен неподвижно; период опускания груза.

Период подъема груза. При подъеме груза червяк 1, червячное колесо 4 и грузовая звездочка 3 вращаются по направлению стрелок 1. Грузовой момент, имея постоянное направление, через червяк 7 прижимает конус 2 (или диски) (рисунки 6.1 и 6.2) тормоза к храповику 1 (рисунок 6.2) с внутренней конической поверхностью: при этом происходит стормаживание частей тормоза. Замкнутый тормоз, вращаясь (стрелка 1) вместе с валом червяка, не встречает препятствий со стороны собачки 4 (рисунок 6.2), т.к. она скользит по скошенным поверхностям зубьев храпового колеса (1).

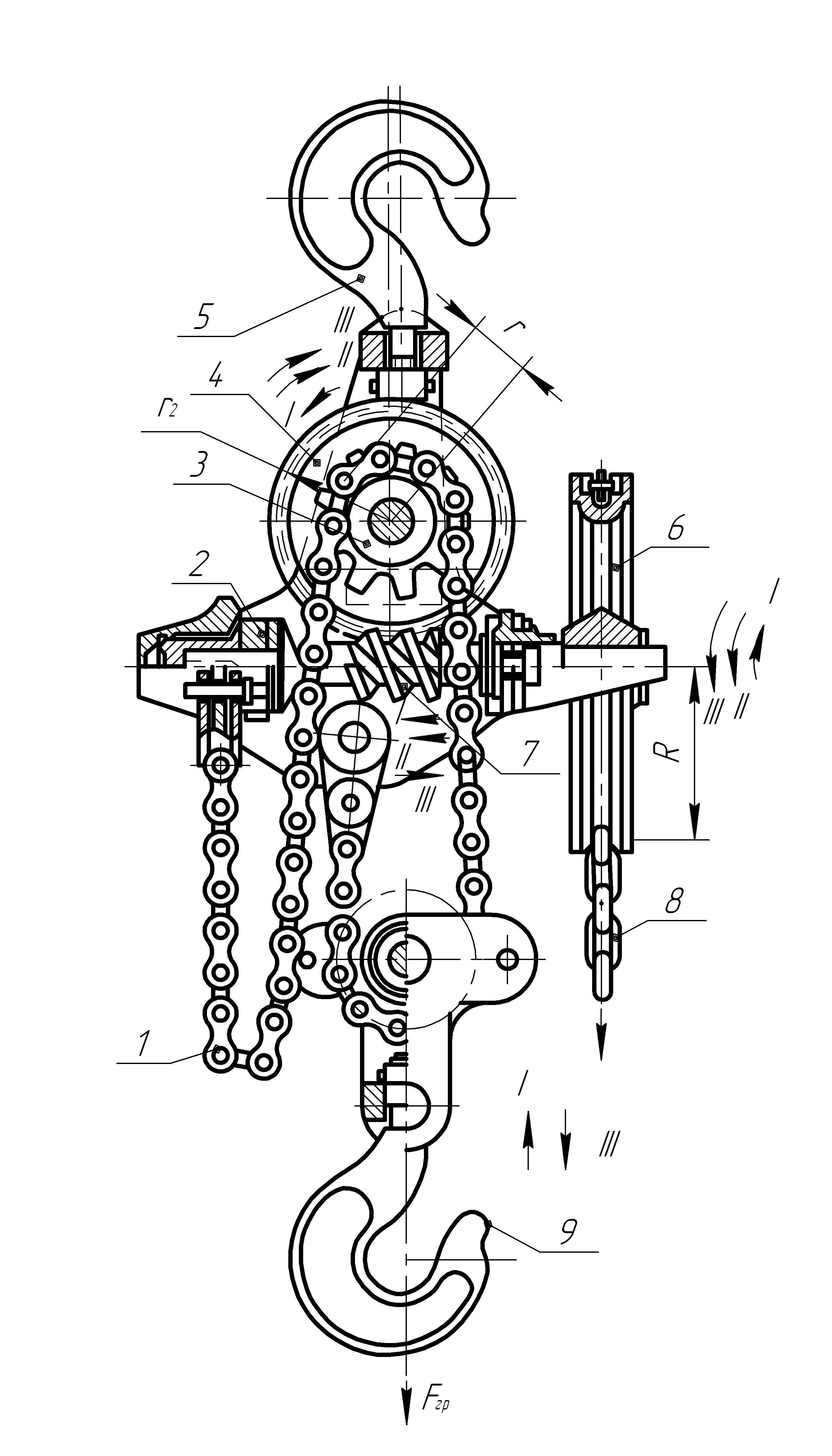
Рисунок 6.1 — Ручная червячная таль; подъём – I; стопор – II; спуск – III

1 — цепь; 2 — конус; 3 — грузовая звездочка; 4 — червячное колесо; 5 — крюк;

6 — тяговая звездочка; 7 — червяк; 8 — тяговая цепь; 9 — крюковая подвеска

Период удержания груза. Как только прекращается вращение тяговой звездочки 6 (рисунок 6.1), вся система стремится в обратном направлении (стрелки ІІ) под действием силы тяжести груза F_гр. Груз стремится опускаться. Но грузовой момент (стрелка ІІ) продолжает удерживать тормоз в замкнутом положении. Т.к. при этом собачка 4 (рисунок 6.2) заскакивает в гнездо между зубьями храпового колеса І, она будет препятствовать обратному вращению системы и груз не сможет опускаться, оставаясь в подвешенном состоянии. Относительное вращение между конусом 2 (или диском 5) и неподвижным храповым колесом І (или 6) будет отсутствовать, т.к. момент тормоза Т_т, стремящейся удержать груз, больше момента статического от груза Т , стремящегося опустить груз, в К_т раз, где К_т = 1,2–1,3 — запас торможения для тормозов осевого действия. Разомкнуть этот тормоз нельзя, поэтому для опускания груза необходимо затрачивать энергию на преодоление запаса тормозного момента.

Период опускания груза. Прикладывая определенное усилие F к тяговой цепи 8 (рисунок 6.1), вращаем тяговую звездочку 6, червяк 7, червячное колесо 4, грузовую звездочку 3 в направлении, обратном подъему (стрелки ІІІ). Сбегающая ветвь грузовой цепи І, которая находится в зацеплении с грузовой звездочкой 3, опускается вместе с крюковой подвеской 9. Происходит опускание груза.

Усилие F, прикладываемое к тяговой цепи 8, связано с преодолением запаса торможения. Т.е. при опускании груза необходимо преодолеть трение между вращающимся конусом 2 (или диском 5) (рисунок 6.2), с одной стороны, и неподвижным колесом І (или 6) — с другой. Храповое колесо І (или 6) неподвижно, т.к. его удерживает собачка 4. Обычно усилие F для опускания груза мало, т.к. коэффициент запаса торможения К_т = 1,2–1,3. Такой малый запас торможения объясняется тем, что в отличие от колодочных и ленточных тормозов, где К_т = 1,5–2,5, данный конусный или дисковый тормоз является автоматическим. Это означает, что по мере увеличения грузоподъемности Q автоматически во столько же раз увеличивается осевое усилие червяка, обеспечивающее прижатие конуса 2 (или диска 5) (рисунок 6.2) к храповому колесу І (или 6) и поэтому во столько раз увеличивается момент тормоза, из-за чего груз никогда не падает.

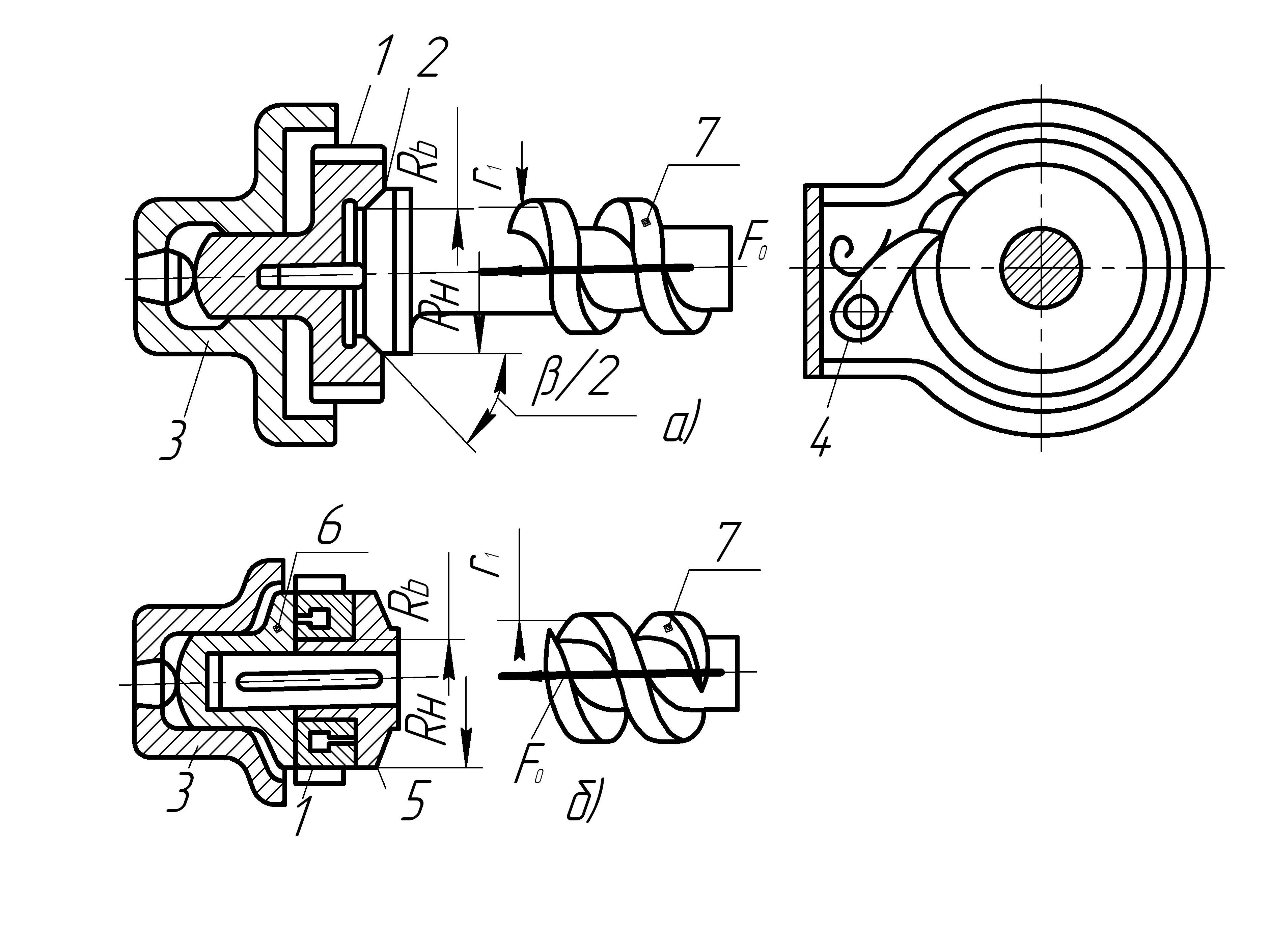
Рисунок 6.2 — Тормоза, замыкаемые под действием транспортируемого груза

а — конусный; б — дисковый.

1 — храповое колесо; 2 — конус; 3 — опоры; 4 — собачка; 5, 6 — диски; 7 — червяк

Величина усилия рабочего при опускании определяется следующим образом:

, (6.1)

тогда

, (6.2)

где — статический момент, создаваемый грузом на валу тормоза (червяка), стремящийся опустить груз.

, (6.3)

где — вес груза, Н;

— диаметр грузовой звездочки, м;

— кратность полиспаста;

— передаточное число червячной передачи;

— КПД полиспаста;

— КПД грузовой звездочки;

— КПД червячной передачи.

Таким образом, при опускании груза необходимо преодолеть разницу между моментом тормоза , удерживающим груз, и моментом статическим от груза, стремящимся опустить груз. А так как момент тормоза мало отличается от момента статического, то остается только преодолеть сравнительно небольшое усилие. Нельзя допускать, чтобы к тяговой цепи прикладывалось какое-либо усилие при опускании груза ( = I). Это означает, что груз может сам произвольно опускать под действием собственного веса, что может привести к несчастному случаю. Поэтому запас торможения не может равняться единице ( ≠ I), а должен быть больше единицы.