10. Подготовка имитационной модели сау.

Подготовить имитационную модель системы автоматического управления. Выполнить моделирования процесса включения системы питания при нулевых начальных условиях для заданных преподавателем величин коэффициентов Кd и Кр.

Схема имитационной модели:

1

BLT 103

101

4

BLT 135

5

BLT 133

6

BLT 133

7

BLT 135

401

501

601

701

8

BLT 103

801

301

2

BLT 133

3

BLT 089

9

BLT 014

10

BLT 015

701

201

х

1) BLT 103 – генератор кусочно-постоянного сигнала (Е₀)

2) BLT 133 – инерционное звено I-ого порядка (нагрузка)

3) BLT 089 – пропорциональное звено (датчик)

4) BLT 135 – сумматор

5) BLT 133 – инерционное звено I-ого порядка (регулятор)

6 BLT 133 – инерционное звено I-ого порядка (исполнительный механизм)

7) BLT 135 – сумматор

8) BLT 103 – генератор кусочно-постоянного сигнала (Х_уст)

9) BLT 014 – осциллограф

10) BLT 015 – табулятор

11) BLT 089 – пропорциональное звено (корректирующее звено)

По условию поставленной задачи необходимо, чтобы цепи регулирования системы были низковольтными, поэтому выбираем Kd = 0.1 и Кр = 10 (эта точка принадлежит области устойчивости)

Смоделируем процесс по схеме, приведённой выше при Кd = 0.1 и Кр = 10:

Х1 – сигнал на выходе основного источника

Х2 – сигнал на выходе нагрузки (регулируемая величина)

Х6 – сигнал на выходе исполнительного механизма

Х8 – сигнал на выходе уставки

Данные результаты нас не устраивают, так как ЭДС регулируемого источника в установившемся режиме не равна нулю, а регулируемая величина не равна уставке. Следовательно, структурно-алгоритмическая схема нашей системы нуждается в корректировке.

11. Корректировка и расчёт основных параметров системы

Выбрать значения коэффициентов К_р и К_д из области устойчивости, которые в статическом режиме обеспечивают нулевую величину ЭДС Е_р регулируемого источника. По результатам эксперимента рассчитать статизм и для выбранных значений коэффициентов К_р и К_д. Рассчитать теоретические значения указанных показателей.

Причиной некорректной работы системы, проиллюстрированной в п. 10, является несогласованность схемы сравнения регулируемой величины с уставкой: датчик ослабляет в 10 раз (Кd = 0.1) сигнал с выхода нагрузки, а уставка выдаёт сигнал той величины, которой должен быть сигнал на выходе нагрузки. В результате на исполнительный механизм поступает ложный сигнал рассогласования и система работает неправильно. Это можно исправить введением после уставки пропорционального звена, коэффициент передачи которого будет равен коэффициенту передачи датчика:

Е₀

8

1

Х_уст

Е₀

11

4

5

6

7

2

W_р

W_им

W_н

Х_уст

Δх

Х_р

Е_р

х

W_кр

–

3

W_д

Промоделируем процесс в скорректированной системе с теми же величинами Кd = 0.1 и

Кр = 10:

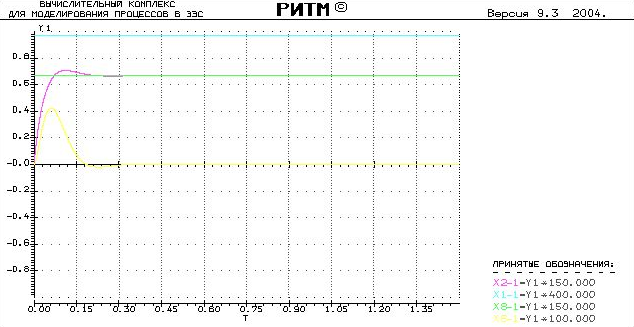
Х1 – сигнал на выходе основного источника

Х2 – сигнал на выходе нагрузки (регулируемая величина)

Х6 – сигнал на выходе исполнительного механизма

Х8 – сигнал на выходе уставки

Как видно по результатам проведённого опыта, мы смогли добиться нулевой ЭДС регулируемого источника и равенства регулируемой величины уставке в установившемся режиме.

Рассчитаем теоретические значения параметров системы:

1). Статизм

2). Перерегулирование

a₀ = 287; a₁ = 27.22*10³; a₂ = 82.96*10⁴; a₃ = 4.1152*10⁶ К_р К_д+8*10⁶

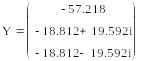
3). Длительность переходного процесса

Экспериментальные статизм, перерегулирование и длительность переходного процесса можно найти из опыта п. 12, в котором имитируется потеря 50 % ЭДС, т. е. изменение воздействия, что и требуется для опытного вычисления статизма.