8. Структурно-алгоритмическая схема сау

Составить структурно-алгоритмическую схему системы автоматического управления

1

Е₀

Е₀

8

4

5

6

7

2

W_р

W_им

Х_уст

W_н

Х_уст

Δх

Х_р

Е_р

х

–

3

W_д

После преобразования:

Е₀

х

Х_уст

W₃₄

W_э

где:

Полученное значение передаточной функции эквивалентированной структурно – алгоритмической схемы САУ имеет вид:

а). относительно источника ЭДС Е₀:

б). относительно сигнала уставки:

9. Построение области устойчивости системы в плоскости коэффициентов Кр и Кд

Построить область устойчивости системы в плоскости коэффициентов К_р и К_д, где

К_р  —коэффициент передачи звена, эквивалентирующего регулятор

К_д — коэффициент передачи звена, эквивалентирующего датчик текущего значения регулируемой переменной

Полученное значение передаточной функции эквивалентированной структурно – алгоритмической схемы САУ:

Характеристическое уравнение найдем, приравняв к нулю знаменатель передаточной функции: D(λ) = R(λ)

Отсюда характеристическое уравнение будет иметь вид:

При подстановке известных характеристик элементов цепи регулирования получим:

a₀ = 287; a₁ = 27.22*10³; a₂ = 82.96*10⁴; a₃ = 4.1152*10⁶ К_р К_д+8*10⁶

Условия нарушения устойчивости:

1). появление нулевого корня

2). выход пары комплексных корней на мнимую ось

По 1-му условию имеем:

Граница области устойчивости для 2-го условия рассчитывается исходя из равенства нулю предпоследнего минора (Δ_n-1 = 0) определителя Гурвица.

Составим определитель Гурвица:

Предпоследний минор:

Приравняв полученное выражение к нулю, получим:

На основе полученных уравнений строим области устойчивости:

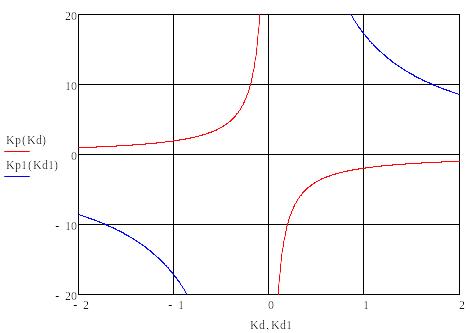
1 2 3

4 5

Проверим, какие из этих областей являются устойчивыми. Для этого выберем точку в каждой из областей и воспользуемся критерием Гурвица. Для устойчивости системы необходима и достаточна положительность определителя Гурвица и всех его миноров.

Область 1:

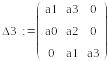
Область неустойчива.

Область 2:

Область устойчива

Область 3:

Область неустойчива

Область 4:

Область неустойчива

Область 5:

Область неустойчива

Таким образом, область 2 является единственной областью устойчивости для данной САУ.