Погрешности измерений.
Для приближенной оценки погрешности
используют понятие действительн6ого
значения физической величины. Получаемую
оценку погрешности, представляющую
собой разность ∆ между полученным при
измерении и действительным значением
физической величины. Погрешность
представлена суммой двух составляющих,
называемых случайной
и систематической
погрешностями измерений:
(1.9.)
СИСТЕМАТИЧЕСКАЯ ПОГРЕШНОСТЬ - составляющая погрешности измерения, оставляющая постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Обнаруженная и оцененная систематическая погрешность исключается из результата введением поправки. В зависимости от причины возникновения различают следующие систематические погрешности.
Погрешность метода измерений- погрешность, обусловленная несовершенством метода измерений.
Инструментальная погрешность – составляющая погрешность измерения, зависящая от погрешности применяемых средств измерений.
- погрешность конструкции
- погрешность технологическая
- погрешность старения
Погрешность установки – следствие неправильности установки средств измерений.
Погрешность от влияющих величин – следствие воздействия на объект и средством измерений внешних факторов (электрических, гравитационных полей, атмосферное давление)
Субъективная погрешность – обусловлена индивидуальными свойствами человека, выполняющего измерения.
По характеру проявления:
-погрешность постоянная;
-погрешность переменная
А) погрешность прогрессивная
Б) погрешность периодическая
В) погрешность, изменяющаяся по сложному закону.
СЛУЧАЙНАЯ ПОГРЕШНОСТЬ – составляющая погрешности измерения, изменяющая случайным образом при повторных измерения одной и той же величины.
Случайная величина погрешность определяется факторами, проявляющимися нерегулярно с изменяющейся интенсивностью. Случайная погрешность не может быть исключена из результата измерений.
Для определения случайной погрешности создаются такие условия, характеризующиеся тем, что интенсивность всех действующих факторов доводиться до некоторого уровня, обеспечивающего более или менее равное влияние на формирование погрешности. В это случае говорят ОЖИДАЕМОЙ ПОГРЕШНОСТИ. Кроме этой погрешности имеют место грубые погрешности и промахи.
ГРУБОЙ ПОГРЕШНОСТЬЮ называют погрешность измерения, существенно превышающую ожидаемую при данных условиях. Причинами грубых погрешностей могут являться неисправность средств измерений, резкое изменение условий измерений и влияющих величин.
ПРОМАХ – погрешность измерения, которая явно и резко искажает результат. Его появление – следствие неправильных действий экспериментатора.
Отдельное значение случайной погрешности предсказать невозможно. Совокупность же случайных погрешностей какого-то измерения одной и той же величины подчиняется определенным закономерностям, которые являются вероятностными. Они описываются с помощью методов теории вероятностей и математической статистики. При этом результат измерения, который содержит случайную погрешность и физическую величину, рассматривают как случайную величину.
Для количественной оценки объективной возможности появления того или иного значения случайной величины служит понятие вероятности, которую выражают в долях единицы (вероятность достоверного события=1, а вероятность не возможного события =0).
Математическое описание непрерывных случайных величин осуществляется обычно с помощью дифференциальных законов распределения случайной величины. Эти законы определяют связь между возможными значениями случайной величины и соответствующими им плотностями вероятностей.
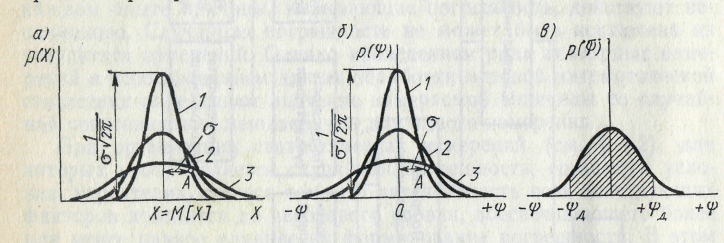Наиболее
распространенным при измерениях является
нормальный закон распределения. Для
некоторой измеряемой величины Х кривая
1 распределения плотности вероятности
р(Х) для закона нормального распределения
имеет вид, показанный на рис. 1.9 а.
Плотность вероятности для закона нормального распределения описывается уравнением:
(1.10)
Где М(Х) и
- характеристики нормального распределения.
Если перенести начало координат в точку Х=М(Х), то в этом случае плотность вероятности
(1.11)
Где
-
случайная погрешность, М(Х) – математическое
ожидание,
- среднеквадратичное отклонение. Они
являются важными числовыми характеристиками.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ – значение величины, вокруг которого группируются результаты отдельных наблюдений:
(1.12.)
СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ – рассеяние отдельных наблюдений относительно математического ожидания, т.е. форма кривой распределения плотности вероятности, площадь под которой всегда равна единице:
(1.13)
На рис.1.9 б. показаны кривые закона нормального распределения случайной величины Х и ее случайной погрешности рис.1.9 б. при различных значениях среднеквадратичного отклонения; рассеяние для кривой 3, больше, чем рассеяние для кривой 2, а рассеяние для кривой 2 –больше, чем кривой 1.
Геометрически определяется как расстояние от оси симметрии нормального распределения до точки А перегиба кривой распределения рис. 1.9 а и 1.9 б.
Чтобы определить вероятность Р попадания
результата измерения или случайной
погрешности в некоторый наперед заданный
интервал от -
до +
(рис.1.9.в), необходимо найти площадь под
кривой распределения, ограниченную
вертикалями на границе интервала. Для
нормального распределения:
(1.14)
Решить интеграл аналитически невозможно. Чаще решается обратная задача, состоящая в определении доверительного интервала. ДОВЕРИТЕЛЬНЫМ ИНТЕРВАЛОМ - с границами называют интервал, который с заданной вероятностью Рд называемой ДОВЕРИТЕЛЬНОЙ, накрывают истинное значение измеряемой величины.
Наиболее часто применяемым в практике обработки результатов измерений для нормального закона распределения является значение доверительной вероятности для значений доверительного интервала, равных 2/3 ; 2 ; 3 . Значение доверительных вероятностей для них соответственно равны 0,500; 0,950; 0,997 рис.1.10.
Рис.1.10 Кривая нормального распределения случайной величины.
Это значит, что случайная погрешность
при одноразовом измерении не выйдет за
пределы интервала
с вероятностью =0,68, т.е. 68 % измерений
будут иметь погрешность
.
Часто встречающимся в измерительной практике законом распределения случайной погрешности является РАВНОМЕРНЫЙ ЗАКОН, когда непрерывная случайная величина имеет возможные значения в пределах некоторого конечного интервала, причем в пределах этого интервала все значения случайной величины обладают одной и той же плотностью вероятности рис.1.11 а.:
0 при
;
(1.15)
Графическая интерпретация закона распределения, называемого двухмодальным, показан на рис.1.11 б.
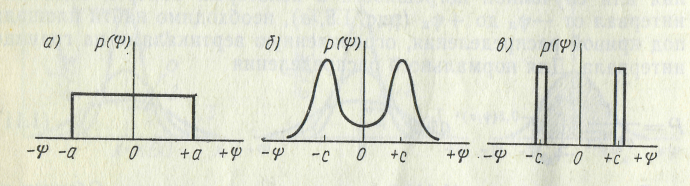
В соответствии с этим законом малые
погрешности встречаются реже, чем
большие. Середина кривой распределения
плотности вероятности оказывается
прогнутой вниз. В пределе такое
двухмодальное распределение может
превратиться в распределение, показанное
на рис. 1.11 в. когда единственно наблюдаемыми
погрешностями будут погрешности
.
Такое распределение называют дискретным.
Появление двухмодального распределения обычно вызвано явлением люфта.