Разностная аппроксимация дифференциальных уравнений и граничных условий при расчете электрических и магнитных полей.

Процедура аппроксимации производных, входящих в дифференциальные уравнения, использует представление аппроксимируемой величины в окрестности рассматриваемой точки поля, где она и ее младшие пространственные производные являются непрерывными, в виде отрезка ряда Тейлора. Рассмотрим сначала эту процедуру для получения разностной аппроксимации уравнения Пуассона, записанного в декартовой системе координат, описывающего плоскопараллельные электрические и магнитные поля: 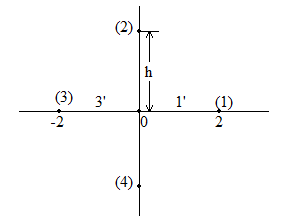Рис.19.

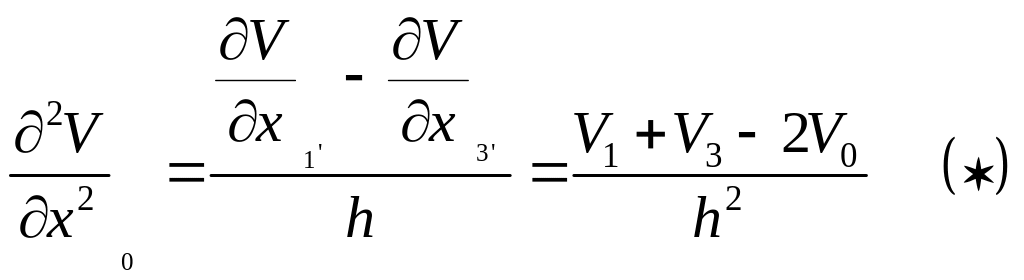
Аналогично записывается

Уравнения подставляем в уравнение Пуассона:

,где k –количество квадратов около обмотки.

.

Выражение для расчета в точках не принадлежащих обмотке, за исключением точек принадлежащих линиям кроме точки . Для них в уравнение в водят . Для точки . То есть и . Для внутренних узлов области расчета не принадлежащих обмотке: . Для узлов принадлежащих границе области ферромагнетика . Расчеты основаны на граничных условиях для . Рассчитывается при помощью закона полного тока.

Рассмотрим внутреннюю точку на линии

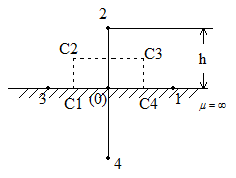Рис.20.

.

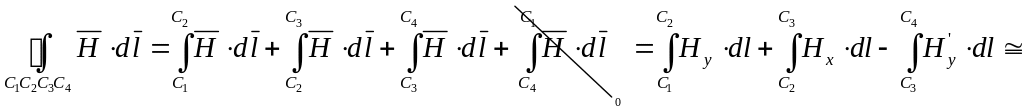
- по закону полного тока, то . То есть наблюдается закономерность для числителя : если точка находится в воздухе ,то она берется с двойным коэффициентом ,если она находится на поверхности , то с коэффициентом равным единице и если точка находится области ферромагнитного сердечника, то она берется с нулевым коэффициентом. Для знаменателя будет просто сумма этих коэффициентов.

И так, для узла : ; Для узлов на линии : ;

Для узла : ;

Для узлов линий и : ;

Для узлов линий : ;

Для узла : ;

Для узла : .

Расчеты в программе POLUS. а) толщина средней обмотки 0,02 м. (по Рис.21.). Таблица № 5 Функция потока.

0	0	0	342.2	326.6	302.0	289.0	285.0
0	0	0	332.8	318.5	296.2	284.6	280.9
0	0	0	302.1	293.6	279.8	272.1	269.6
0	0	0	263.3	261.4	257.3	254.3	253.3
0	0	0	228.4	231.3	233.6	234.7	235.1
0	0	0	187.7	201.9	211.0	215.9	217.5
0	52.5	110.8	153.2	177.7	192.5	200.5	203.0
0	49.6	97.6	136.4	163.4	180.8	190.4	193.5
0	48.2	93.7	131.3	158.7	176.8	187.0	190.3

б) толщина средней обмотки 0,04 м. (по Рис.22.).

Таблица № 6. Функция потока.

0	0	0	326.6	322.2	308.1	293.9	289.5
0	0	0	318.5	314.6	301.8	289.0	285.1
0	0	0	293.2	290.9	283.2	275.3	272.7
0	0	0	260.2	260.1	258.4	256.2	255.3
0	0	0	227.3	230.8	234.1	235.8	236.3
0	0	0	187.4	201.8	211.3	216.5	218.2
0	52.5	110.8	153.1	177.8	192.7	200.9	203.5
0	49.6	97.6	136.4	163.5	181.0	190.8	193.9
0	48.2	93.7	131.3	158.9	177.1	187.3	190.6

Индуктивность толстой обмотки.

Вычисление энергии магнитного поля в объеме на основе выражение сопряжено с большими затруднениями, так как необходимо рассчитать напряженность и индукцию магнитного поля во всех точках бесконечного пространства. Вычисление энергии магнитного поля можно упростить, если преобразовать интеграл по неограниченному объему V в интеграл по объему , в котором существует создающий магнитное поле электрический ток плотностью .

Для такого преобразования воспользуемся соотношением и известным из векторной алгебры выражение , или . После подстановки в формулу для энергии магнитного поля выражения вместо имеем

Можно показать, что второе слагаемо в стремится к нулю, поэтому

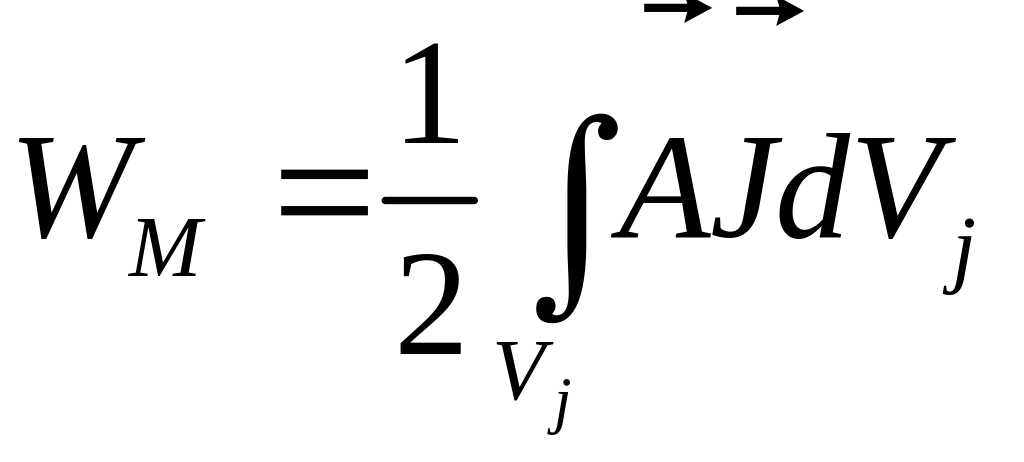
Что позволяет ограничить вычисление интеграла лишь в той части объема, в которой плотность электрического тока не равна нулю.

, где = ширина сердечника ,V-объем области занятой обмоткой.

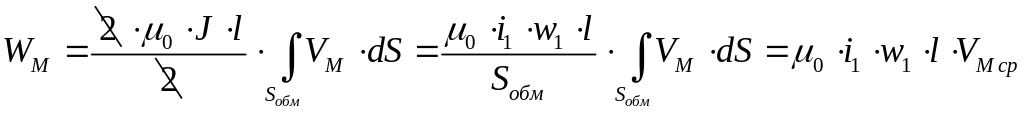
, где - среднее значение узлов принадлежащих обмотке.

.

Для случая а):

Для случая б):

Чем больше толщина обмотки, тем меньше индуктивность .

Рис.21. Картина плоскопараллельного магнитного поля для толщины обмотки 2 см

(по данным табл. №5).

Рис.22. Картина плоскопараллельного магнитного поля для толщины обмотки 4 см

(по данным табл. №5).

Список использованной литературы

1. К.С. Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л.Чечурин, Теретические основы электротехники, 4-е издание, том 3.-СПб.:Питер, 2003. - 337с.

2. М.А.Шакиров, Р.П. Кияткин, В.С. Лопатин и др.; Под ред. проф. М.А. Шакирова. Практикум по ТОЭ. Ч.3.-CПб.: СПБГТУ. 1995.-168с.

3. А.Б.Новгородцев, А.Н.Модулина, Р.П.Кияткин, Теоретические основы электротехники. Расчеты по теории электромагнитного поля. -СПб.: СпбГПУ,2008.

47