2. Зависимость распределения потенциала, максимальной напряжённости и ёмкости от варьируемого параметра

   1. Распределение потенциала между слоями.

Пределы варьирования параметра:

_и

_{Следовательно,получаем:}

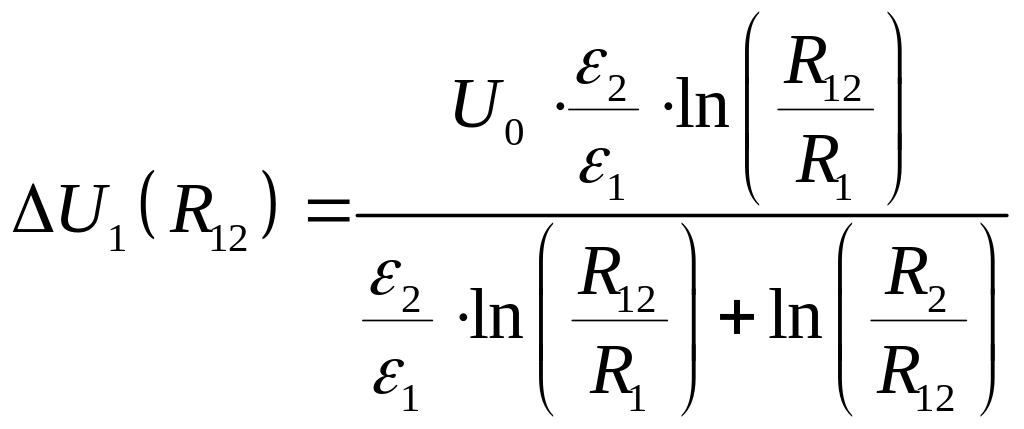
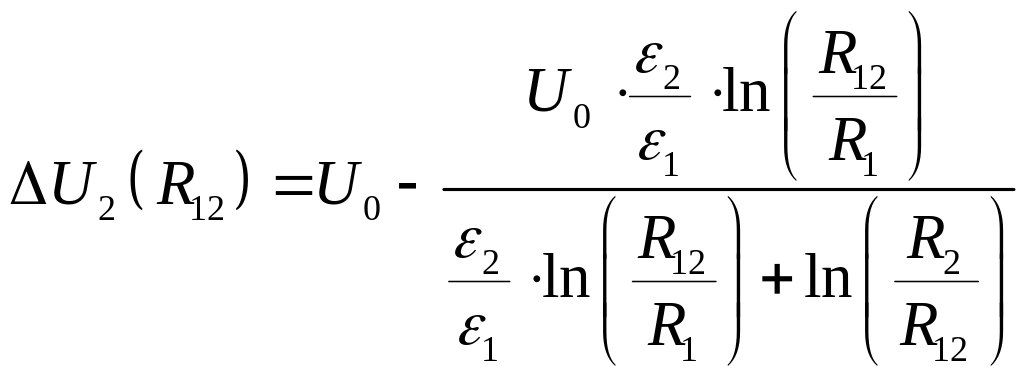
Примеры расчета для расстояния :

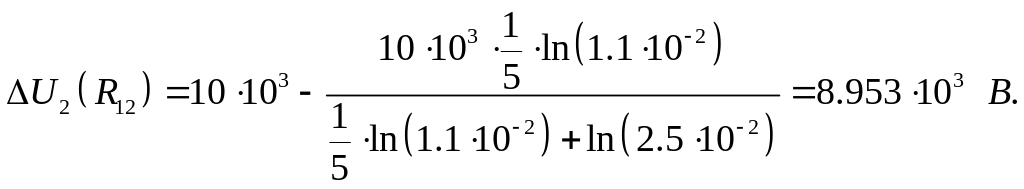
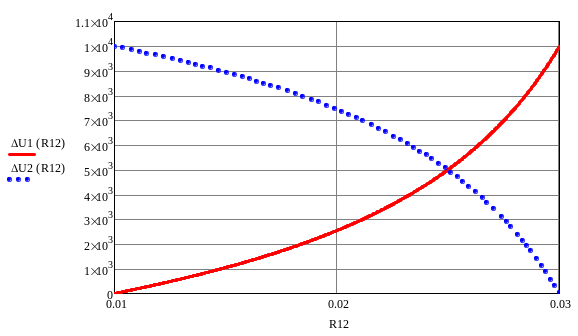
Рис.3. График зависимости распределения потенциала.

2. Определение максимальной напряженности.

Определение максимальной напряжённости: По графику видно (Рис.1.), что наибольшая напряженность наблюдается в точке на расстоянии со стороны второй области, т.е.:

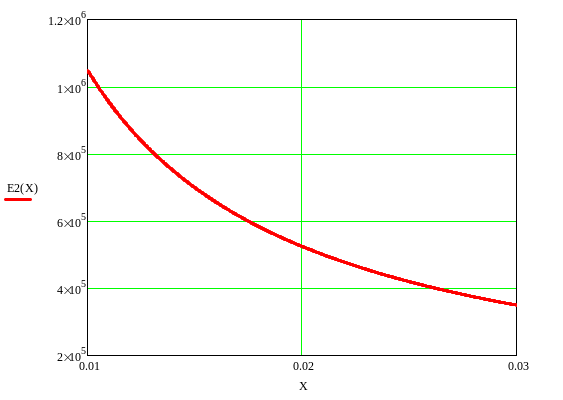
Рис4.График распределения максимальной напряжённости.

3. Определение ёмкости конденсатора (ёмкость на единицу длины).

Ёмкость конденсатора:

Постулат Максвелла в интегральной форме

Расчёт заряда (внутренней обкладки)

S-поверхность интегрирования: цилиндр срадиусом ,соосный с кабелем, охватывающим жилу.

Так как диэлектрик однородный

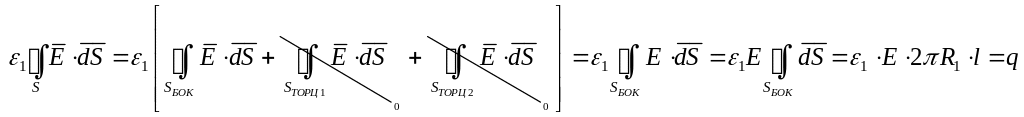
(так как )

На поверхности интегрирования

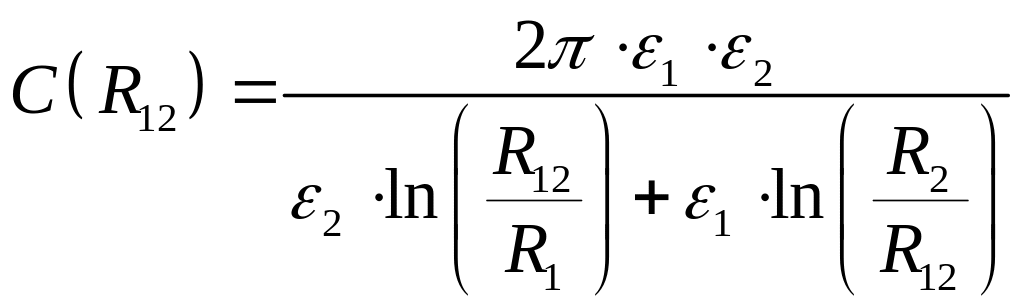
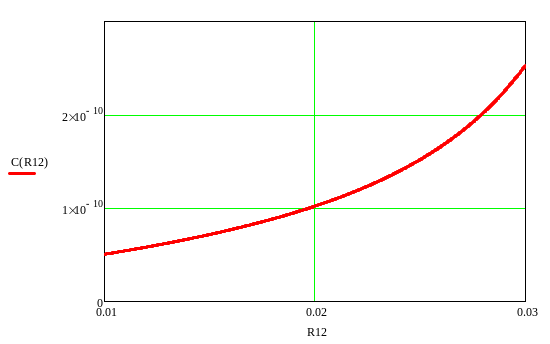
Рис5.График зависимости распределения ёмкости.

Пример расчета для расстояния :

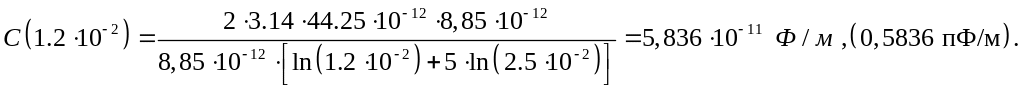
2. Определение , при котором потенциал делится поровну между слоями.

Так как по условию, то

Выразим :

Теперь можем найти :

м.

II. Расчет плоскопараллельного поля линейного заряда над заземленной поверхностью. Задание: Заряженный провод с линейной плотностью τ (τ/ε₀ =1) расположен вблизи заземленной поверхности. Диаметр провода d = 1см. Область расчета поля D_Z имеет вид, соответствующий рисунку. Параметр области . Координата оси провода: м.

1. Обозначив точки границы поверхности буквами (A, B, C и т.д.), проверить, переходят ли они в точки на оси вещественных в плоскости ω при использовании отображающей функции ω(z)=z^π/b

2. Рассчитать поверхностную плотность (σ) заряда, индуцированного на проводящих поверхностях (в 5 точках каждой поверхности) и построить эпюры распределения σ. Привести пример расчета σ в одной точке.

3. Полагая число линий равного потенциала равным 4, а число трубок равного потока равным 8, построить по 32-м расчетным точкам картину плоскопараллельного поля в области D_Z. Картину следует построить на листе миллиметровки формата А4.

4. Считая данный провод одним из проводов трехфазной линии передачи, рассчитать емкость С системы на фазу. Провода трехфазной линии расположены на одной прямой на расстоянии 20см друг от друга.

5. Полученное в п.4 значение емкости С сравнить с приближенным значением, рассчитанным без учета влияния земли.

Теоретическая часть

Расчет плоскопараллельного поля линейного заряда над заземленной поверхностью.

1. Плоскопараллельное поле – поле системы из нескольких бесконечно длинных параллельных друг другу цилиндрических проводов с зарядами, равномерно распределенными по их длине. Все линии напряженности поля лежат в плоскостях, параллельных плоскости XOY. Потенциал плоскопараллельного поля есть функция только двух координат x и y. Поверхности равного потенциала – цилиндрические поверхности с образующими, параллельными оси 0z. Лини равного потенциала определяются уравнением вида U(x,y)= const.

Функция V(x,y) – функция потока, определяющая совокупность всех точек , лежащих на одной и той же линии напряженности поля и V(x,y) = const является уравнением линии напряженности поля.

Уравнения U(x,y)= const и V(x,y) = const определяют два семейства кривых, пересекающихся всюду под прямым углом т.е образующих ортогональную сетку.

2. Комплексный потенциал поля – функция, вещественная часть некоторой есть функция потока, а мнимая – потенциал.

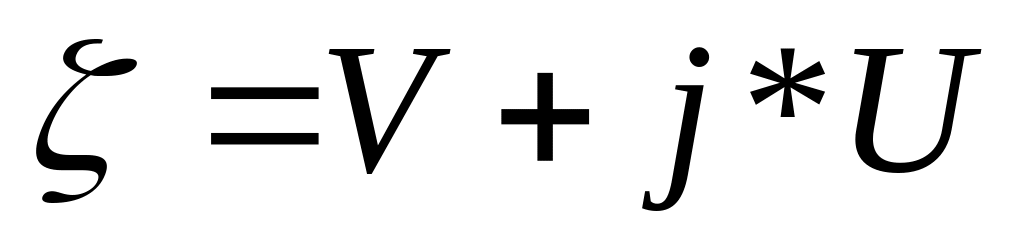
Для вычисления Е имеем соотношение:

3. Поле уединенного провода круглого сечения:

Функция определяет поле, линии напряженности которого являются лучами, исходящими из начала координат. Линии равного потенциала являются окружностями с центром в начале координат, и поверхности равного потенциала - поверхностями круговых цилиндров. /Если совместить с одной из этих поверхностей поверхность заряженного провода кругового сечения, то для поверхности провода будет удовлетворено основное требование – постоянство потенциала. Следовательно, можно утверждать, что рассматриваемая функция является комплексным потенциалом поля вне провода.

4. Графический метод построения картины плоскопараллельного поля

Для построения плоскопараллельного поля должны соблюдаться следующие условия:

1. линии напряженности поля и линии равного потенциала должны пересекаться всюду под прямым углом

2. линии напряженности поля должны быть перпендикулярны к контурам, ограничивающим сечения проводников

3. ячейки сетки, образованной линиями напряженности поля и линиями равного потенциала, при достаточной густоте сетки должны быть приблизительно подобны друг другу.

5. Метод зеркальных изображений

Если заменить проводящую среду зеркальным изображением провода с изменением знака заряда, то в области над проводящей средой поле останется таким же, как и в действительных условиях. Этот метод применим при любом числе проводов, протянутых параллельно друг другу и параллельно плоской поверхности, ограничивающей проводящую среду. Каждый провод должен быть зеркально отображен в поверхности проводящей среды с изменением знака заряда, после чего проводящая среда может быть мысленно удалена и рассмотрено поле совокупности действительных проводов и их зеркальных изображений. В таком поле плоскость, расположенная на месте поверхности проводящей среды, является поверхностью равного потенциала, так как заряды противоположных знаков размещены симметрично относительно этой плоскости. Следовательно, найденное таким путем поле и будет действительным полем в области над поверхностью проводящей среды.

6. Потенциальные коэффициенты, коэффициенты электростатической индукции и частичные емкости в системе тел.

Коэффициенты α носят название потенциальных коэффициентов. Они зависят от формы и размеров поверхностей тел, от взаимного расположения тел и от диэлектрической проницаемости среды. Коэффициенты αkk с одинаковым коэффициентом называются собственными потенциальными коэффициентами. Коэффициенты β называются коэффициентами электростатической индукции- собственными при одинаковых индексах и взаимными при разных индексах. Они имеют размерность емкости.

1. Конформное преобразование (Рис.6. и Рис.7.).

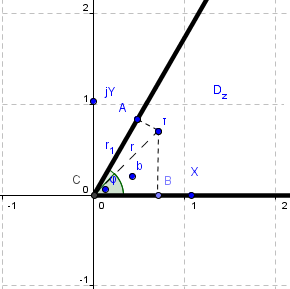
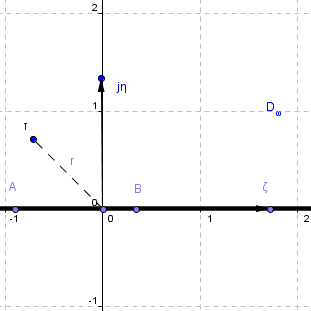
Рис.6. В области . Рис.7. В области .

Отображающие функции:

Переведём область в область

Где , наикратчайшее расстояние до наклонной

стенки .

	А	0	B

Таблица 1. Результаты конформного преобразования.