Расчет стальных вертикальных резервуаров

Расчет резервуара сводится к подбору его толщины стенки по поясам по безмоментной теории последующей проверке ее на устойчивость от действия боковых и осевых нагрузок. Основной эксплуатационной нагрузкой на стен­ку вертикального цилиндрического резервуара является гидростатическое давление столба жидкости и избыточное давление, при котором продукт хра­нится.

Определение толщины стенки ведется по формуле, получаемой для час­того случая цилиндрических замкнутых безмоментных тонкостенных оболо­чек, находящихся под внутренним равномерным давлением из известного уравнения Лапласа:

(10.1)

где n₁ – коэффициент перегрузки от действия гидростатического давле­ния (n₁ =1,1);

n₂ – коэффициент перегрузки от действия избыточного давления (n₂= 1,2);

γ – удельный вес продукта, Н/м3;

Н – высота резервуара, м;

х – расстояние по вертикали от днища до начала рассчитываемого пояса, м;

р_изб – избыточное давление в газовом пространстве резервуара, Па;

r – радиус резервуара, м;

k – коэффициент безопасности по материалу (k=0,9);

т – коэффициент условий работы;

R – расчетное сопротивление стали растяжению-сжатию, Па.

Р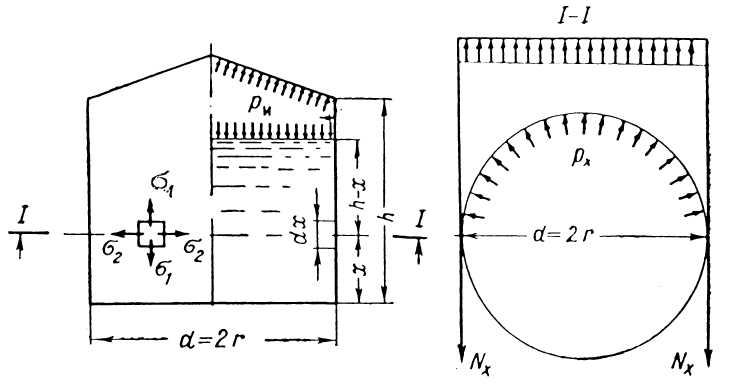 ис. 10.1. Расчетная схема вертикального цилиндрического резервуара

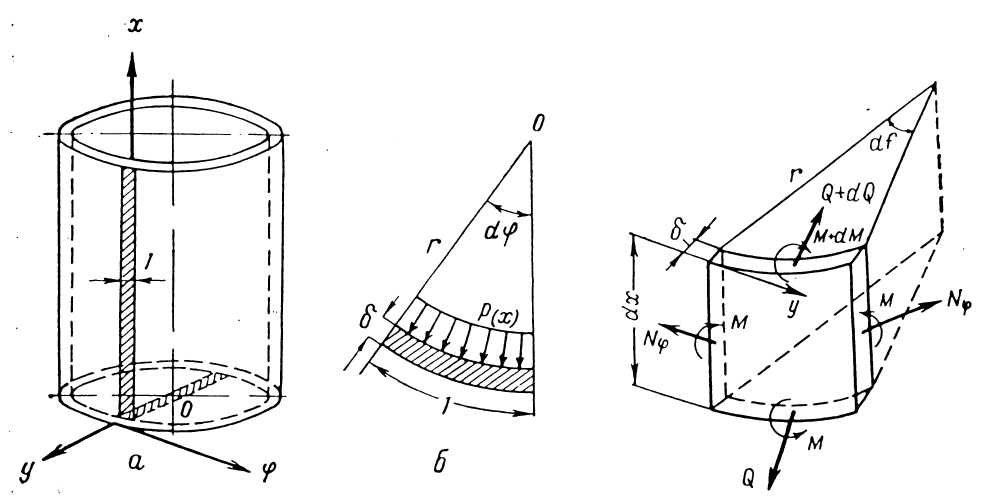
Рисунок 10.2. Усилия, действующие на элемент оболочки

ВОПРОС №13

Расчет узла сопряжения стенки резервуара с днищем при упругом опирании на песчаную подушку

Для нахождения напряжений в упорном, наиболее нагруженном сварном шве, составляется и решается уравнение совместности деформаций стенки и днища.

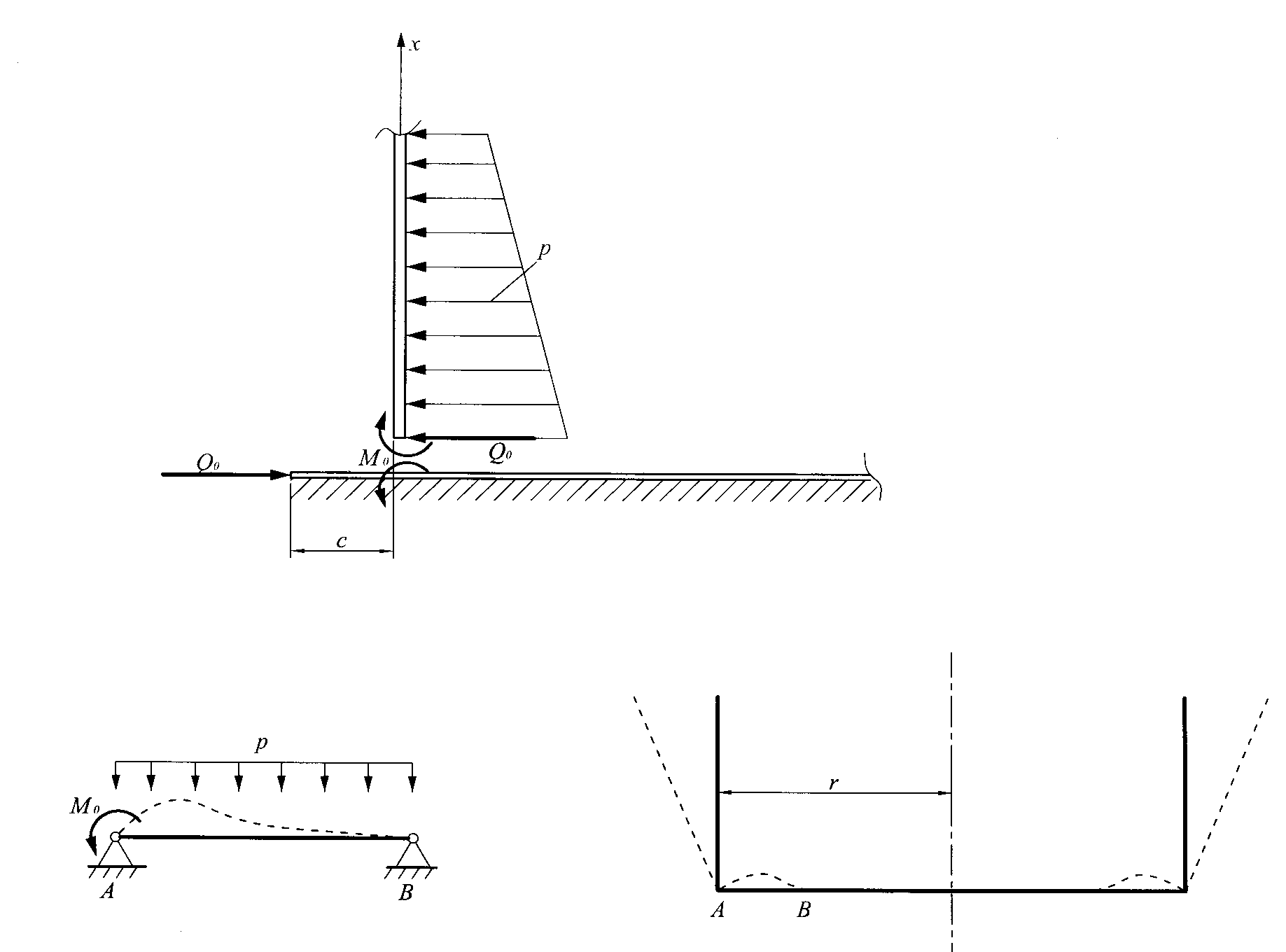
Рис. 10.3. Расчетная схема узла сопряжения стенки и днища

Канонические уравнения метода сил записываются следующим образом

, (10.2)

где перемещения соответственно стенки и днища под действием единичных сил;

грузовые коэффициенты метода сил;

изгибающий момент и поперечная сила в защемлении.

Перемещения стенки определяются из решения дифференциального уравнения четвертого порядка изгиба цилиндрической оболочки

, (10.3)

где прогиб;

определяется выражением ;

– цилиндрическая жесткость.

При решении дифференциального уравнения пользуются гиперболо-тригонометрическими функциями , , , . В результате получают значения коэффициентов канонических уравнений метода сил

, , , (10.4)

, . (10.5)

Те же коэффициенты, выражающие перемещения днища, вызванные воздействием нагрузки q – от веса стенки и покрытия

, (10.6)

от изгибающего момента М₀

(10.7)

от гидростатического давления

. (10.8)

После подстановки найденных коэффициентов в систему уравнений, определяют М₀ и Q₀, а затем отыскивают возникающие напряжения в шве, соединяющем стенку с днищем и строят эпюру изгибающих моментов.

ВОПРОС №14