Cтатистические методы.

Статистические методы наиболее часто в практике анализа работы рудников и обогатительных фабрик применяются для установления следующих зависимостей:

- величины капитальных и эксплуатационных затрат на добычу и переработку от производственной мощности предприятия или других важных факторов, в т.ч. горно-геологических;

- показателей обогащения добываемой рудной массы (извлечение в концентраты и содержание в концентратах различных полезных компонентов) в зависимости от содержания в ней полезных и вредных компонентов;

- производительности выпуска руды и погрузочно-транспортных средств в зависимости от cтепени дробления руды и других факторов;

- выход негабаритов или затраты на вторичное дробление в зависимости от параметров буровзрывных работ и удельного расхода ВВ на отбойку;

- производительности бурения в зависимости от глубины, диаметра скважины и др. факторов.

Применительно к условиям рудников наиболее распространенные эмпирические зависимости, установленные на основе статистических методов, имеют вид линейной, степенной и полиномиальной функций

у = а + bх; ; .

Кроме выбора вида функций необходимо определить входящие в нее постоянные величины а, b и с. Наиболее часто для этого применяется метод наименьших квадратов.

Метод наименьших квадратов основан на отыскании минимума суммы квадратов отклонений реальных, полученных опытом, данных от теоретических (расчетных), т.е., когда

,

где у_j - фактические значения исследуемого показателя; - расчетные значения, вычисленные по предполагаемому уравнению; n - число реализаций ряда.

Например, для линейной функции у = а + bх:

Дифференцируя выражение по а и в и приравняв оба уравнения к 0, получим систему

Решив эту систему, получим искомые коэффициенты уравнения.

После установления характера зависимости и ее параметров должна быть осуществлена весьма ответственная процедура анализа полученной зависимости с точки зрения ее надежности и объективности.

Теснота связи оценивается коэффициентом корреляции

,

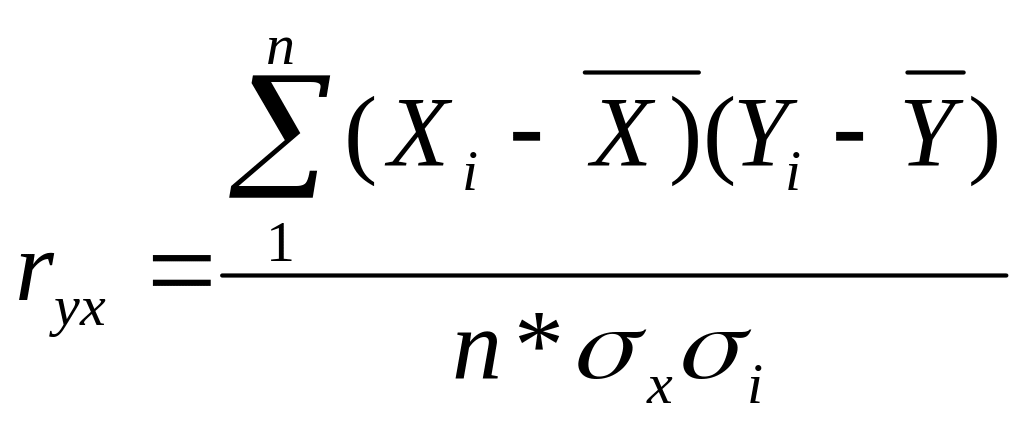Если r=0.6-1.0- связь сильная, r=0,3-0.6 – связь средняя и менее 0.3- связь слабая и недостоверная.

Несмотря на простоту и универсальность статистические методы при проектировании рудников могут применяться лишь в качестве вспомогательных и для решения частных задач. Для обработки данных и выявления эмпирических зависимостей при решении частных вопросов (выбор параметров БВР, определение производительности погрузки, выпуска и доставки, зависимости между потерями и разубоживанием руды, необходимые для нормирования этих показателей использования недр, зависимости между содержанием металлов в добываемых полезных ископаемых и показателями извлечения их при переработке и т.п.).

Методы прогнозирования.

Методы прогнозирования при проектировании рудников применяются для определения основных направлений технического прогресса, вероятного изменения сырьевой базы развития отрасли, производственной мощности рудника и других возможных изменений техники, технологии и технико-экономических показателей рудников в будущем. Использование данных прогноза при проектировании очень важно для выбора прогрессивной технологии и установления технико-экономических показателей.

Прогноз - это вероятностное суждение о состоянии какого-либо объекта (процесса или явления) в определенный момент времени в будущем (или) альтернативных путях достижения каких-либо результатов. Прогнозирование - это процесс формирования прогнозов развития объекта на основе анализа тенденций его развития.

В отличие от планирования при прогнозировании в связи с большими сроками прогнозов имеет место более высокая степень неопределенности вырабатываемой информации.

Основные этапы прогнозирования - это ретроскопия, диагноз (анализ) объекта и проспекция. На стадии ретроскопии осуществляется сбор, хранение, и обработка информации, оптимизация методов измерения и самой информации, на основе чего формируется структура и состав характеристик объекта прогнозирования.

На стадии диагноза осуществляется анализ объекта прогнозирования и составляется прогнозная модель.

При анализе сложного объекта используются теории информации, теория измерений, распознавания образов. Эти методы помогают выбрать важнейшие, ведущие переменные (факторы), минимизировать размерности описания, выбрать адекватные шкалы для измерения количественных и качественных изменений. Математические методы, применяемые при прогнозировании, основаны на теории вероятности и математической статистике, теории численных методов, анализа, теории факторного анализа.

Наиболее распространенными методами прогнозирования являются экстраполяционные (сглаживания и уравнивания статистического ряда, экстраполяция простыми зависимостями с использованием степенных полиномов, экстраполяция тенденций по огибающим кривым и др.), статистические (корреляционный и регрессионный анализы, факторный анализ), экспертные, переработки патентной информации, технологического моделирования и др.

По степени детерминированности можно выделить объекты:

1) детерминированные, в которых случайной составляющей можно с достаточной точностью пренебречь;

2) стохастические, в описании которых необходим учет случайной составляющей переменных в соответствии с требуемой точностью и задачей прогноза;

3) cмешанное, имеющее характеристики детерминированные и стохастические.

Какой-либо процесс или показатель можно представить в виде переменного ряда У_t выражением

У_t = X_t + _t

где Х_t - детерминированная составляющая процесса (тренд); _t - случайная (стохастическая) составляющая процесса.

Прогнозное значение величины У_t определяется суммой прогнозных значений тренда и случайной составляющей. Если известна функция тренда, то задача определения детерминированной составляющей решается. Если неизвестна, то надо установить подходящий для данной задачи вид тренда. Обычно из ряда функций, представляющих собой прямые, параболы, степенные функции и т.п. наиболее простым и распространенным методом является метод наименьших квадратов, ранее рассмотренный.

При прогнозировании применяются также методы экспоненциального сглаживания, метод скользящей средней и др.