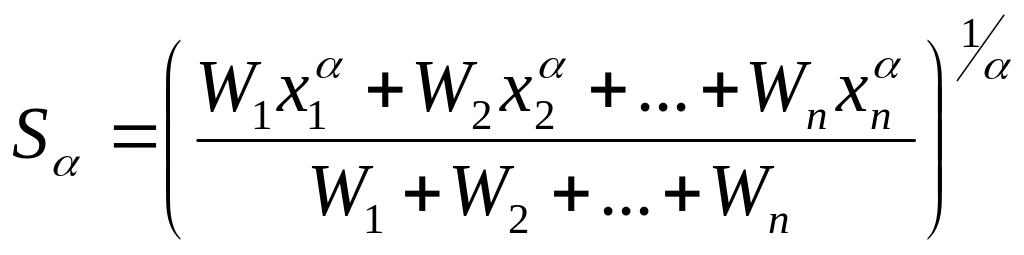3.6. Нормальное распределение

Распределение вероятностей случайной величины X называется нормальным, если оно имеет плотность распределения вероятностей:

(16)

где M_x - математическое ожидание случайной величины X, σ² - генеральная дисперсия. Математическое ожидание и дисперсия полностью определяют расположение и форму кривой y=f(x; M_x, σ). График плотности нормального распределения называется нормальной кривой или кривой Гаусса. Кривая нормального распределения y=f(x; M_x, σ) симметрична относительно ординаты, проходящей через точку x=M_x, и имеет в этой точке единственный максимум, равный . Квадратный корень из дисперсии называется стандартным отклонением. Обозначается греческой буквой σ. Вероятное отклонение для нормального распределения равно 2/3σ≈0,6745σ. Перегибы кривой наблюдаются при значениях x=M_x-σ и x=M_x+σ. Площадь, заключённая под кривой нормального распределения равна единице, - это означает достоверность события принятия случайной величиной любого значения в интервале от до + .

Закон нормального распределения вероятностей наиболее важен и широко распространен в природе. Множество событий, происходящих в природе, происходят случайно в результате одновременного влияния на развитие события большого числа независимых детерминированных причин (факторов), из которых максимальная по величине мала по сравнению со всей суммой. Достаточно часто нормальное распределение является предельным законом для суммы большого числа детерминированных воздействий, каждое из которых подчинено своему закону распределения. По сравнению со всеми другими распределениями нормальное распределение содержит минимум информации о явлении, чем любое другое распределение с тем же средним значением и дисперсией. Другими словами, замена исследуемого распределения эквивалентным нормальным не может привести к переоценке точности наблюдений.

Согласно закону нормального распределения, вероятность того, что случайная величина примет значение в интервале равна 0,683, вероятность попадания в интервал равна 0,954, а . Последнее соотношение называется правилом трёх сигма. Что оно означает? То, что на практике, при принятии решений относительно возможных результатов событий, подчиняющихся закону нормального распределения, пренебрегают возможностью отклонений от M_x, превышающих 3σ (соответствующая вероятность меньше 0,003).

3.7. Основные характеристики распределений

Известно, что закон распределения вероятностей полностью определяет случайную величину. Однако, промысловые данные и др. обычно представлены в виде таблиц. При таком представлении данных сравнивать их между собой не просто. Для визуального сравнения распределений удобны гистограммы распределений или кривые плотности вероятностей p(x) и функции вероятностей F(x).

Для сравнения различных распределений на количественном уровне удобно выразить характерные особенности распределения при помощи числовых характеристик, называемых моментами случайной величины. Моменты распределения полностью характеризуют само распределение, следовательно, ими можно пользоваться для количественного сопоставления распределений.

Для непрерывной случайной величины начальный момент β-того порядка выражается формулой:

(17)

Начальный момент нулевого порядка, или нулевой начальный момент

(18)

Он характеризует площадь, находящуюся под кривой распределения

Начальный момент первого порядка или первый начальный момент

является оценкой математического ожидания или средним значением случайной величины X. Оценка математического ожидания, m_x, для непрерывной случайной величины определяется формулой:

(19)

Математическое ожидание, среднее значение, - одна из важнейших числовых характеристик распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность значений x₁, x₂,..., x_i,... с вероятностями, равными соответственно p₁, p₂,..., p_i,... , математическое ожидание определяется:

для дискретной случайной величины формулой:

(20)

для непрерывной случайной величины формулой:

(21)

Математическое ожидание характеризует наиболее вероятное расположение значений случайной величины.

Существуют несколько способов оценки математического ожидания по результатам выборки, но только некоторые из них используются практически. В большинстве случаев важно знать среднее значение выборки или совокупности, на практике используются три вида среднего значения, - мода, медиана и среднее арифметическое. Максимуму кривой плотности вероятностей соответствует мода, это наиболее вероятный результат. Если распределение асимметрично, то иногда представляет интерес медиана, - то значение случайной величины, которое делит распределение на две равные части. Другими словами, вероятности событий по обе стороны медианы одинаковы. Следующим средним значением является среднее арифметическое, его проще всех вычислить и, отчасти по этой причине, оно нашло наиболее широкое применение. Кроме этого, в условиях нормального распределения арифметическое среднее имеет наименьшую дисперсию. В условиях асимметричных кривых распределения медиана расположена между модой и средним арифметическим.

В науке и технике кроме арифметического среднего применяют также:

геометрическое среднее

(22)

гармоническое среднее

(23)

квадратичное среднее

(24)

Если все числа x₁, x₂,..., x_n, положительны, то можно для любого α≠ο определить степенное среднее

(25)

Арифметическое, гармоническое и квадратичное среднее являются частными случаями степенного среднего, а именно, s_α равно x_ср, x_h и x_s соответственно при α=1, -1 и 2. При α→0 степенное среднее s_α стремится к геометрическому среднему: s₀→x_g. Если , то ; в частности, .

Наряду со степенными средними применяются взвешенные степенные средние:

(26)

В частности, при α=1

(27)

которые переходят в обыкновенные степенные средние при W₁=W₂=...=W_n.

В науке и технике находит применение также арифметико-геометрическое среднее.

Арифметико-геометрическое среднее - общий предел последовательностей арифметического среднего x_ср,n и геометрического среднего x_g,n получаемых в результате следующих операций. Для пары положительных чисел a и b вычисляют арифметическое среднее x_ср,1 и геометрическое среднее x_g,1. Далее, для пары x_ср,1 и x_g,1 снова вычисляют арифметическое среднее x_ср,2 и геометрическое среднее x_g,2 и т.д. В результате получают последовательность чисел x_ср,n и x_g,n, n=1, 2,...

Поскольку математическое ожидание M_x определяет центр группирования случайной величины, в точку m_x переносят начало координат. Случайные величины, отсчитываемые от центра группирования m_x называются центрированными, а моменты центрированной случайной величины - центральными.

Центральный момент β-го порядка для непрерывной случайной величины определяется формулой:

(28)

Очевидно, что нулевой центральный момент μ₁=1 и выражает площадь под кривой распределения.

Первый центральный момент μ₁=0, - математическое ожидание центрированной величины равно нулю.

Второй центральный момент характеризует рассеяние случайной величины относительно среднего значения и называется дисперсией, обозначаемой . Для непрерывной случайной величины:

(29)

Дисперсия (< лат. disperse - рассеянно, разбросанно, там и сям; dispersio - рассеяние, разбросанность) в математической статистике и теории вероятностей - одна из характеристик распределения вероятностей случайной величины, наиболее употребительная мера рассеяния её значений, т.е. отклонения её от среднего; дисперсия - центральный момент второго порядка. Для случайной величины X с непрерывным распределением, имеющим плотность вероятности p(x), дисперсия определяется формулой

(30)

если этот интеграл сходится. Дисперсия имеет важное значение в характеристике качества статистической оценки случайной величины. Наряду с дисперсией в качестве меры рассеяния (той же размерности, что и сама случайная величина) используется квадратный корень из дисперсии: σ = , называется квадратичным отклонением X. Если DX=0, то случайная величина X принимает с вероятностью 1 единственное значение M_x. Поскольку в реальной жизни математическое ожидание - величина неизвестная, на практике определяют среднее значение выборки и выборочную дисперсию:

(31)

(32)

где n_оп - число опытов в выборке, ν_оп=n_оп-1 - число степеней свободы выборочной дисперсии.

Для оценки результатов наблюдений одной дисперсии недостаточно. Корень квадратный из дисперсии называется квадратичным отклонением, стандартным отклонением или стандартом. Для интерпретации как дисперсии, так и стандартного отклонения главное не получить численные значения последних, а правильно сравнить дисперсию исследуемой выборки с какой-либо другой дисперсией, или стандартное отклонение умножить на правильно выбранный критерий Стьюдента, чтобы получить доверительный интервал для неизвестного математического ожидания.

Поскольку нормальное распределение весьма важно и широко распространено в природе, с ним принято сравнивать экспериментально полученные распределения. Для сравнения экспериментального распределения и более полного его описания применяют моменты высших порядков.

Третий центральный момент характеризует "скошенность" или асимметрию распределения:

(33)

Безразмерный коэффициент асимметрии вычисляется по формуле:

(34)

Для нормального распределения A_x=0.

Четвертый центральный момент характеризует "крутость" распределения, т.е. островершинность или плосковершинность распределения

(35)

Безразмерный коэффициент, описывающий эти свойства, называется эксцессом:

(36)

В уравнении (36) число 3 вычитается потому, что для распределения Гаусса отношение μ₄/σ⁴_x=3. Следовательно, для нормального распределения эксцесс E_x=0.