1. Случайные процессы

1.1. Функция распределения случайного процесса

Д етерминированный процесс полностью определяется значением аргумента . Для случайного процесса нельзя задать однозначное соответствие между аргументом и значениями функции. Одному значению аргумента может соответствовать множество значений функции, одни из которых более вероятны, другие - менее вероятны. Случайный процесс - это функция времени, которая при любом значении времени есть случайная величина. Во время эксперимента наблюдаются конкретные значения случайного процесса , которые называются реализациями случайного процесса. Случайный процесс классифицируют по пространственно-временным признакам и по вероятностным характеристикам.

В общем случае и время , и пространство значений случайного процесса принимают непрерывные значения. Такой процесс называется процессом общего типа, Рис. 1.1.

Если рассматриваются непрерывные значения времени , а значения случайного процесса дискретны, то такой процесс называется дискретным процессом, Рис. 1.2. Если время принимает дискретные значения, а значения случайного процесса непрерывны, то такой процесс называется последовательностью общего типа, Рис. 1.3.

Если время принимает дискретные значения и значения случайного процесса тоже дискретны, то такой процесс называется дискретной случайной последовательностью, Рис. 1.4.

Для всех типов случайных процессов необходимо задать (определить) область возможных значений случайного процесса . В частности, случайный процесс может принимать значения в интервале , т.е. .

Рассмотрим реализаций случайного процесса в момент времени (Рис 1.5) и зададим некоторый порог

t

t

t

t

. Из множества реализаций выберем те реализаций, значения которых не превышают . Отношение называется частотой появления реализаций, значения которых в момент t₁ не превышают величины .

Для различных частота будет различной, но с увеличением она стабилизируется, приближаясь к некоторой постоянной величине. В теории вероятностей доказывается, что при неограниченном увеличении числа независимых реализаций частота будет сколь угодно мало отличаться от вероятности того, что наблюдаемые значения случайного процесса в момент не превышают некоторой постоянной величины . Эта вероятность зависит от величины , времени и называется одномерной функцией распределения случайного процесса

(1.1)

Точно по такой же методике можно составить многомерную функцию распределения

, (1.2)

отражающую вероятность того, что значения случайного процесса в моменты времени не превысят соответствующих значений .

Таким образом, случайный процесс можно описать многомерной функцией распределения (1.2). Чем больше точек отсчета функции распределения, тем более полно описан случайный процесс. Необходимое количество точек отсчета в исследуемой функции распределения зависит от решаемой проблемы.

Для процесса общего типа и для последовательности общего типа вводится одномерная плотность распределения вероятности:

(1.3)

или многомерная плотность распределения вероятности,

. (1.4)

Используя формулы (1.3) и (1.4) , запишем интегральные формы одномерной и многомерной функций распределения

, (1.5)

(1.6)

Для дискретного процесса и дискретной случайной последовательности вводится совместная вероятность того, что случайный процесс находится в состояниях в моменты времени :

. (1.7)

Одномерная и многомерная функции распределения дискретного процесса и дискретной случайной последовательности будут иметь вид

,

, (1.8)

где - значения случайного процесса на дискретном множестве .

Функция распределения вероятности обладает свойствами:

1. функция распределения является неубывающей функцией, т.е. если , то ,

,

2. , ,

, .

3.

4.

Если - дискретный случайный процесс, то процесс описывается вероятностью - реализаци ности дискретного случайного процесса определена как

Плотность распределения вероятности обладает следующим свойствами:

1. плотность распределения– неотрицательная функция

, . . . , ,

2. должно соблюдаться условие нормировки

,

.

3. теорема умножения

,

где , ( ), - плотность распределения вероятности случайного процесса в момент при условии, что в моменты времени известны значения процесса .

4. ,

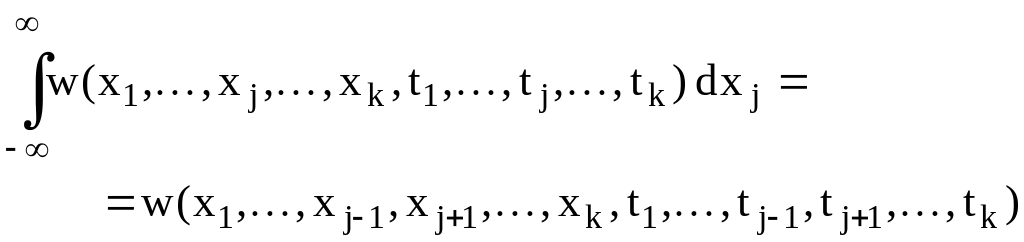
5. Размерность одномерной плотности распределения вероятности - , размерность многомерной плотности распределения вероятности - , где - размерность измеряемой величины (ток, напряжение, давление и т.д.).