37. Навести визначення, кістякове дерево зв'язаного неорієнтованого графа.

Кістякове дерево зв'язаного неорієнтованого графа — ациклічний зв'язний підграф цього графа, який містить всі його вершини]. Неформально кажучи, кістякове дерево складається з деякої підмножини ребер графа, таких, що рухаючись цими ребрами можна з будь-якої вершини графа потрапити до будь-якої іншої.

Кістякове дерево також називають каркасним деревом, покриваючим деревом, кістяком або каркасом графа.

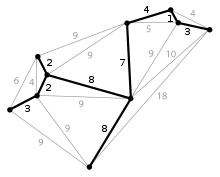
властивості: Будь-яке каркасне дерево у графі з n вершинами містить рівно n — 1 ребро. Кількість кістякових дерев у повному графі з n вершинами подається відомою формулою Келі:

У загальному випадку, кількість кістякових дерев у довільному графі може бути обчислено за допомогою так званої матричної теореми про дерева.

Каркасне дерево може бути побудовано майже будь-яким алгоритмом обходу графа, наприклад пошуком у глибину або у ширину. Воно складається з усіх пар ребер (u, v), таких, що алгоритм, переглядаючи вершину u виявляє в її списку суміжності нову, невиявлену раніше вершину v. Кістякове дерево, побудоване обходом графа починаючи з вершини s за алгоритмом Дейкстри, має властивість, що найкоротший шлях у графі з вершини s до будь-якої іншої вершини — це шлях з s до цієї вершини в побудованому дереві.

Існує кілька паралельних і розподілених алгоритмів пошуку каркасного дерева. Як практичний приклад розподіленого алгоритму можна навести протокол STP.

Якщо кожному ребру графа присвоєно вагу, то пошук оптимального каркасного дерева, яке мінімізує суму ваги його ребер здійснюють численні алгоритми пошуку мінімального каркасного дерева.

Задача про пошук кістяка, в якому ступінь кожної вершини не перевищує деякої наперед заданої константи k, є NP-повною.

38. Сформулювати завдання про знаходження мінімального кістякового дерева

1.На площині задано N точок. Знайти дві з них, відстань між якими найменша.

1.1. На площині задано N точок. Побудувтаи дерево, вершинами якого є всі задані точки і сумарна довжина якого усіх ребер мінімальна.

39. Розкрити алгоритм Краскала.

Алгоритм Крускала (или алгоритм Краскала) — алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом в 1956 году. Вначале текущее множество рёбер устанавливается пустым. Затем, пока это возможно, проводится следующая операция: из всех рёбер, добавление которых к уже имеющемуся множеству не вызовет появление в нём цикла, выбирается ребро минимального веса и добавляется к уже имеющемуся множеству. Когда таких рёбер больше нет, алгоритм завершён. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным деревом минимального веса. До начала работы алгоритма необходимо отсортировать рёбра по весу, это требует O(E × log(E)) времени. После чего компоненты связности удобно хранить в виде системы непересекающихся множеств. Все операции в таком случае займут O(E × α(E, V)), где α — функция, обратная к функции Аккермана. Поскольку для любых практических задач α(E, V) < 5, то можно принять её за константу, таким образом общее время работы алгоритма Крускала можно принять за O(E * log(E)).

Алгоритм:

Спочатку ребра сортують за зростанням ваги.

Додають в дерево ребро з найменшою вагою

Зі списку ребер із найменшою вагою вибирають нове безпечне ребро

Це ребро додають у дерево і знову переходять до кроку 3.

Робота закінчується, коли всі вершини будуть у дереві.