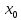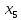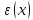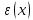Казанский (Приволжский) федеральный университет
Институт вычислительной математики и информационных технологий
Кафедра системного анализа и информационных технологий
Семестровая работа по курсу «Численные методы»:
Интерполирование трансцендентных функций
Вариант 3
Работу выполнила:
студент 3 курса
Группы 09-761
Обрезаненко В.С.
Работу проверила:
Доцент
Глазырина Л. Л.
Казань 2019
Содержание
Постановка задачи 3
Задание 1 4
4
Задание 2 5
Задание 3 7
Вывод 9
Листинг программы 10
Список литературы 16
Постановка задачи
Одна из специальных функций математической физики — функция ошибок, определяется следующим образом
Цель задания – изучить и сравнить различные способы приближенного вычисления этой функции.
Для этого:
Протабулировать erf(x)
на отрезке
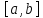с шагом h точностью
,
основываясь на ряде Тейлора, предварительно
вычислив его
где
a
=
0, b
= 2, h
= 0.2,
,
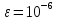и получить, таким образом, таблицу
|
|
|
|
… |
|
|
|
|
|
… |
|
-
По полученной таблице значений построить интерполяционный полином Лагранжа, приближающий
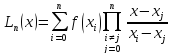
и вычислить погрешность интерполирования
В качестве узлов интерполяции взять:
-
Равномерно распределенные узлы
,
шаг вычисляется через
,
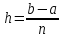где a и b
– границы отрезка. -
Узлы интерполяции Чебышева, вычисляемые по формуле:
.
-
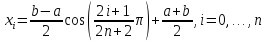Выявить зависимость максимальной погрешности интерполирования от числа узлов интерполяции.
Задание 1
Протабулируем
на отрезке
с шагом h
с
точностью
,
основываясь на ряде Тейлора, предварительно
вычислив его
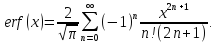
Чтобы
не возникло переполнение при вычислении
факториала, учтем, что каждый член ряда
получается из предыдущего
умножением на некоторую величину
,
т.е.
Табулирование
на отрезке
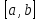с шагом
и точностью
реализуется при помощи отдельной
функции, параметром которой являются
точка x,
в которой вычисляется значение самой
функции.
Ряд
вычисляется с заданной точностью до
тех пор, пока |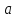
n
(
)|
не будет меньше или равно
,
при
.
Значения
функции
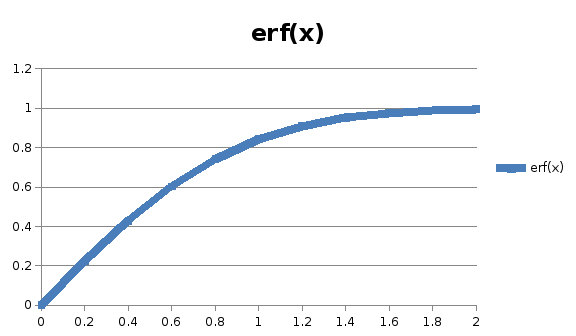
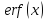График
функции
|
|
F |
|
0 |
0 |
|
0,2 |
0,222702586 |
|
0,4 |
0,428392354 |
|
0,6 |
0,603856097 |
|
0,8 |
0,7421009298 |
|
1 |
0,8427007792 |
|
1,2 |
0,9103140515 |
|
1,4 |
0,952285172 |
|
1,6 |
0,9763484347 |
|
1,8 |
0,9890905681 |
|
2 |
0,9953223747 |
Задание 2
По прибиженной таблице значений построить интерполяционный полином Лагранжа:
и
вычислить погрешность интерполирования
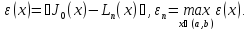
Значения
полинома Лагранжа, построенного по
равнораспределенным узлам (при n=5)
записаны в таблице ниже. При n=5
максимальная по модулю погрешность
равна:
0,0006965558258.
График погрешности полинома по равнораспределенным узлам при n=5:
Значения
полинома Лагранжа, построенного по
чебышевским узлам (n=5).
Максимальная погрешность в данном
случае: max(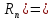
0,004403258497.
График погрешности полинома Лагранжа по чебышевским узлам (n=5):
Задание 3
Необходимо выяснить зависимость максимальной погрешности интерполирования от числа узлов интерполяции. В качестве узлов интерполяции рассмотрим равнораспределенные узлы и корни полинома Чебышева.
График зависимости максимальной погрешности для равнораспределенным узлов:
|
n |
|
|
5 |
0,0006965 |
|
6 |
0,00040089 |
|
7 |
0,000050763 |
|
8 |
1,13972E-05 |
|
9 |
0,00000113 |
|
11 |
1,847E-07 |
|
12 |
1,828E-07 |
|
13 |
0,000000341 |
|
14 |
6,0158E-07 |
|
15 |
1,9789E-06 |
|
24 |
0,000003197 |
|
29 |
0,00001203 |
|
38 |
0,0001702 |
|
39 |
0,000077503 |
|
41 |
0,005866 |
|
42 |
0,0155411 |
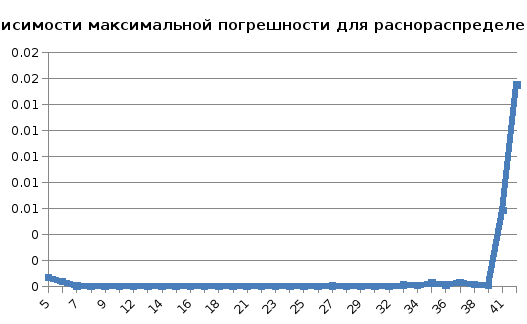
График зависимости максимальной погрешности для корней полинома Чебышева:
|
n |
|
|
5 |
0,000440326 |
|
6 |
0,000200278 |
|
7 |
2,82112E-05 |
|
8 |
8,76107E-06 |
|
9 |
7,27576E-06 |
|
11 |
1,29182E-07 |
|
13 |
1,72171E-07 |
|
35 |
4,33307E-08 |
|
44 |
4,267E-08 |
Вывод
В ходе работы, были построены интерполяционные полинома Лагранжа для функции erf(x) с использованием равнораспределенных узлов интерполяции и корней полинома Чебышева степени n+1.
Сравнивая два построенных полинома убедились, что в случае равнораспределенных узлов интерполяции максимальная по модулю погрешность будет гораздо больше, чем для узлов Чебышева.
Если точка совпадает с узлом интерполяции, то погрешность равна нулю, так как значение функции в этой точке совпадает со значением полинома.
Исследование зависимости максимальной погрешности от числа узлов интерполяции позволяет сделать следующий вывод:
-
При равнораспределенных узлах погрешность уменьшается до тех пор, пока количество узлов не станет равно 41. При таком количестве узлов максимальная погрешность резко увеличивается и далее ведет себя не стабильно (то растет, то снова уменьшается).
-
При узлах Чебышева наблюдается равномерное уменьшение погрешности при увеличении количества узлов интерполяции. Чем больше n, тем меньше погрешность. Она уменьшается до определенного момента и дальше удерживается на примерном значении 3,03838Е-08 (порядок остается одинаковым).