1.6 Коэффициент температурного расширения.
Сжимаемость или расширение жидкости – это ее способность изменять объем при изменении действующих на нее давления или температуры. Это свойство характеризуется коэффициентом температурного расширения βt и объемного сжатия βр .
Коэффициент температурного расширения βt представляет собой число, которое определяет приращение единицы объема жидкости при повышении ее температуры на 1̊ С: βt = (∆V)/V*∆t =(V2-V1)/V1(t2-t1). Объем воды(в отличие от объема других тел) при нагревании от 0 до 4 ̊С уменьшается, так как при этой температуре она имеет наибольшие плотность и удельный вес. Если продолжать нагрев, то объем воды будет увеличиваться. Коэффициент βt воды при нагревании от 0 до 50 ̊С увеличивается с возрастанием давления, при дальнейшем повышении температуры и давления он уменьшается.
1.7 Коэффициент объемного сжатия.
Сжимаемость или расширение жидкости – это ее способность изменять объем при изменении действующих на нее давления или температуры. Это свойство характеризуется коэффициентом температурного расширения βt и объемного сжатия βр .
Капельные жидкости, характеризуются очень малой сжимаемостью. Коэффициент объемного сжатия βр выражает относительное сокращение объема жидкости при увеличении действующего на нее давления р, т.е.: βр = - (∆V)/V*∆t= V1-V2/ (р2-р1)*V1=(1/ρ)*(∆ρ/∆р).
При изменении давления от 0,1 до 50 МПа коэффициент объемного сжатия воды практически остается одинаковым. В связи с этим, при решении многих задач сжимаемостью жидкости обычно пренебрегают.
1.8 Закон Архимеда.
Закон Архимеда — это закон статики жидкостей и газов, согласно которому на тело, погруженное в жидкость (или газ), действует выталкивающая сила (сила Архимеда), равная весу вытесненной этим телом жидкости (или газа).
F
A
= ρgV,
где ρ — плотность жидкости (газа),
g — ускорение свободного падения,
V — объем погруженного тела (или объем той части тела, которую погрузили в жидкость (или газ)).
Архимедова сила направлена всегда противоположно силе тяжести. Она равна нулю, если погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Следует помнить, что в состоянии невесомости закон Архимеда не работает.
Условия плавания тел в жидкостях и газах.
Fт — сила тяжести, FА — сила Архимеда.
Fт = FА — тело плавает в жидкости или газе,
Fт > FА — тело тонет,
Fт < FА — тело всплывает до тех пор, пока не начнет плавать.
ρt — плотность тела, ρs — плотность среды, в которую погрузили тело.
ρt = ρs — тело плавает в жидкости или газе,
ρt > ρs — тело тонет,
ρt < ρs — тело всплывает до тех пор, пока не начнет плавать.
1.9 Приборы для измерения давления
Существует два основных типа приборов для измерения давления в жидкости.
К приборам первого типа можно отнести пьезометры. Они представляют собой вертикальную трубку, обычно прозрачную. Если, например, нужно измерить давление в точке a, то достаточно подсоединить эту трубку к стенке сосуда так чтобы её конец находился на поверхности равного давления, проходящей через эту точку. В пьезометре установится уровень жидкости, пропорциональный давлению в т. a. Абсолютное давление в этой точке будет
С другой стороны, это же давление можно представить как
Отсюда
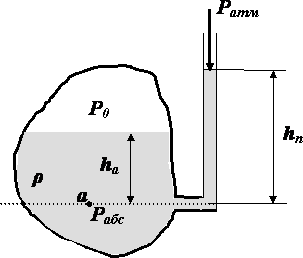
Величина
называется пьезометрической высотой.
По её величине судят о величине давления.
Если
абсолютное давление меньше атмосферного
, то в жидкости имеет место разрежение,
или вакуум. Такое давление называют
вакуумметрическим давлением
, а высоту в пьезометре называют
вакуумметрической высотой
. Эти величины соответственно равны:
и
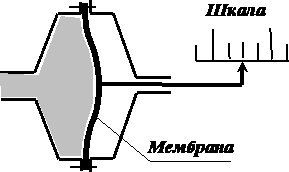
Ко второму типу приборов относятся манометры, которые имеют большое разнообразие по типам размерам и характеристикам. Однако принципиально все эти приборы состоят из чувствительного элемента, который меняет свою форму под воздействием давления, и, связанного с этим элементом, передаточного механизма и регистрирующего прибора (индикатора).
Подсоединять манометры для измерения давления в определённой точке надо также как пьезометры, на уровне поверхности равного с выбранной точкой, давления. Например, под действием давления гибкий чувствительный элемент – мембрана изгибается. Размер этого отклонения пропорционален величине измеряемого давления. Вместе с мембраной отклоняется жёстко соединённая с ней стрелка, которая перемещается вдоль шкалы. Такой прибор отличается небольшим отклонением регистрирующего элемента – стрелки, следовательно, точность измерения большой быть не может. Общим недостатком таких приборов является малое исходное отклонение чувствительного элемента – мембраны.