оценка проектов создания различных организаций массового обслуживания, например центров обработки заказов, заведений быстрого питания, больниц, отделений связи; анализ финансовых и экономических систем и т. д.

Имитационное моделирование - один из наиболее распростра­ненных методов исследования операций и теории управления (а возможно, и самый распространенный метод). Более широкому использованию ИМ препятствовали несколько факторов.

Во-первых, модели, применяемые для исследования больших систем, все более усложняются, что, в свою очередь, затрудняет написание компьютерных программ. В последние годы эту задачу удалось существенно облегчить путем разработки мощных про­граммных продуктов, включающих элементы, необходимые для соз­дания имитационной модели.

Во-вторых, для моделирования сложных систем часто требует­ся много компьютерного времени. Однако по мере увеличения быстродействия и уменьшения стоимости компьютеров эта проб­лема постепенно становится решаемой. ИМ является экспериментальной и прикладной методологией, имеющей целью описать поведение системы, по­строить теории и выдвинуть гипотезы, а также использовать эти теории для предсказания будущего поведения системы. Модель, включающую все аспекты такой классификации, бу­дем называть полной или совершенной имитационной моделью. В соответствии с классификационным признаком полноты моделирование делится на полное, неполное и приближенное. При полном моделировании модели идентичны объекту во времени и пространстве. Для неполного моделирования эта идентичность не сохраняется. В основе приближенного моделирования лежит подобие, при котором некоторые стороны реального объекта не моделируются совсем.

Вопрос 14

Основные преимущества и недостатки имитационного моделирования

Применение имитационных моделей дает множество преимуществ по сравнению с выполнением экспериментов над реальной системой и использованием других методов.

Стоимость. Допустим, компания уволила часть сотрудников, что в дальнейшем привело к снижению качества обслуживания и потери части клиентов. Принять обоснованное решение помогла бы имитационная модель, затраты на применение которой состоят лишь из цены программного обеспечения и стоимости консалтинговых услуг.

Время. В реальности оценить эффективность, например, новой сети распространения продукции или измененной структуры склада можно лишь через месяцы или даже годы. Имитационная модель позволяет определить оптимальность таких изменений за считанные минуты, необходимые для проведения эксперимента. Повторяемость. Современная жизнь требует от организаций быстрой реакции на изменение ситуации на рынке. Например, прогноз объемов спроса продукции должен быть составлен в срок, и его изменения критичны. С помощью имитационной модели можно провести неограниченное количество экспериментов с разными параметрами, чтобы определить наилучший вариант.

Точность. Традиционные расчетные математические методы требуют применения высокой степени абстракции и не учитывают важные детали. Имитационное моделирование позволяет описать структуру системы и её процессы в естественном виде, не прибегая к использованию формул и строгих математических зависимостей.

Наглядность. Имитационная модель обладает возможностями визуализации процесса работы системы во времени, схематичного задания её структуры и выдачи результатов в графическом виде. Это позволяет наглядно представить полученное решение и донести заложенные в него идеи до клиента и коллег.

Универсальность. Имитационное моделирование позволяет решать задачи из любых областей: производства, логистики, финансов, здравоохранения и многих других. В каждом случае модель имитирует, воспроизводит, реальную жизнь и позволяет проводить широкий набор экспериментов без влияния на реальные объекты.

Однако имитационное моделирование наряду с достоинствами имеет и недостатки:

- разработка хорошей имитационной модели часто обходится дороже создания аналитической модели и требует больших временных затрат;

- может оказаться, что имитационная модель неточна (что бывает часто), и мы не в состоянии измерить степень этой неточности;

- зачастую исследователи обращаются к имитационному моделированию, не представляя тех трудностей , с которыми они встретятся и совершают при этом ряд ошибок методологического характера.

И, тем не менее, имитационное моделирование является одним из наиболее широко используемых методов при решении задач синтеза и анализа сложных процессов и систем.

Вопрос 15

Дискретно-событийное моделирование.

Дискретно-событийное моделирование используют для пост­роения модели, отражающей изменение состояния системы, когда переменные изменяются мгновенно в конкретные моменты време­ни. При этом происходят мгновенные события, которые могут изменить состояние системы.)Несмотря на то что теоретически ДСМ можно осуществлять вручную, большое количество данных, которые должны сохраняться и обрабатываться при моделиро­вании реальных систем, обусловливает необходимость примене­ния ЭВМ.

В качестве примера рассмотрим очередь покупателей к при­лавку небольшого магазина подарков (так называемая однолиней­ная система массового обслуживания с одним устройством).

Предположим, что промежутки времени между последовательными появлениями покупателей распределены рав­номерно в интервале от 1 до 10 мин, а время, необходимое для обслуживания каждого покупателя, распределяется равномерно в интервале от 1 до 6 мин. Хозяйку магазина интересует среднее время пребывания покупателя в магазине, а также время (в %), в течение которого продавец, стоящий на контроле, не загружен ра­ботой.

Для моделирования системы необходимо найти способ имита­ции последовательности прибытия покупателей и времени, тре­буемого для обслуживания каждого из них. Один из предполагае­мых способов состоит в том, чтобы взять десять фишек с цифрами от 1 до 10 и один игральный кубик. Положим фишки в шляпу и тщательно ее встряхнем. При вытягивании фишки из шляпы и счи­тывании .выпавшего числа моделируются промежутки времени между приходами предыдущего и последующих покупателей, а при бросании кубика и считывании с его верхней грани выпавшего числа очков определяется время обслуживания каждого покупа­теля. Повторяя эти операции в указанной последовательности (возвращая каждый раз фишки обратно и встряхивая шляпу перед каждым вытягиванием), можно получить временные ряды, пред­ставляющие собой промежутки времени между последовательными прибытиями покупателей и соответствующие им времена обслу­живания. Результаты, полученные в случае посещения 20 покупа­телей, приведены в табл. 1.1.

Таблица 1.1

Окончание табл. 1.1

В результате обработки данных получаем время пребывания покупателя в магазине *_маг = 68/20 = 3,4 мин и время простоя про­давца t_n = [55/(55 + 63)] • 100 % - 47 %.

Очевидно, что для получения статистической значимости ре­зультатов необходимо иметь достаточно большую выборку, учесть ряд таких привходящих нюансов, как начальные условия работы магазина и др., однако приведенный пример носит чисто методи­ческий характер.

Вопрос 16

Непрерывное моделирование — это моделирование системы по времени с помо­щью представления, в котором переменные состояния меняются непрерывно по отношению ко времени. Как правило, в непрерывных имитационных моделях ис­пользуются дифференциальные уравнения, которые устанавливают отношения для скоростей изменения переменных состояния во времени. Если дифференци­альные уравнения очень просты, их можно решать аналитически, чтобы предста­вить значения переменных состояния для всех значений времени как функцию значений переменных состояния в момент времени 0. При больших непрерывных моделях аналитическое решение невозможно, но для численного интегрирования дифференциальных уравнений в случае с заданными специальными значениями для переменных состояния в момент времени 0 используются технологии числен­ного анализа, например интегрирование Рунге-Кутта.

Пример

Рассмотрим непрерывную модель соперничества между двумя популяция­ми. Биологические модели такого типа, именуемые моделями хищник-добыча, рассматривались многими авторами, в том числе Брауном и Гордоном. Среда представлена двумя популяциями -хищников и добычи, взаимодействующими друг с другом. Добыча пассивна, но хищни­ки зависят от ее популяции, поскольку она является для них источником пищи. (Напри­мер, хищниками могут быть акулы, а добычей — рыба, которой они питаются) Пусть x(t) и y(t) обозначают численность особей в популяциях соответственно добычи и хищников в момент времени t. Допустим, популяция добычи имеет обильные запасы пищи; при отсутствии хищников темп ее прироста составит rх(t) для некоторого положительного значения r (r — естественный уровень рождаемости минус естествен­ный уровень смертности). Существование взаимодействия между хищниками и добы­чей дает основание предположить, что уровень смертности добычи в связи с этим взаи­модействием пропорционален произведению численностей обоих популяций х(t)у(t). Поэтому общий темп изменения популяции добычи dx/dt: может быть представлен как

(1)

где а — положительный коэффициент пропорциональности. Поскольку существование самих хищников зависит от популяции добычи, темп изменения популяции хищников в отсутствии добычи составляет -sу(t) для некоторого положительного s. Более того, взаимодействие между двумя популяциями приводит к росту популяции хищников, темп которого также пропорционален х(t)у(t). Следовательно, общий темп изменения популяции хищников dy/dt составляет

(2)

где b — положительный коэффициент пропорциональности. При начальных условиях х(0) > 0 и y(0) >0 решение модели, определенной уравнениями ( 1) и ( 2), имеет инте­ресное свойство: х(t) > 0 и у(t) > 0 для любого t0. Следовательно, попу­ляция добычи никогда не будет полностью уничтожена хищниками. Решение {х(t), у(t)} также является периодической функцией времени. Иными словами, существует такое значение Т>0, при котором х(t + пТ)=x(t) и у(t + пТ) = у(t) для любого положительно­го целого числа п. Такой результат не является неожиданным. По мере увеличения по­пуляции хищников популяция добычи уменьшается. Это приводит к снижению темпа роста популяции хищников и, соответственно, вызывает уменьшение их числа, что, в свою очередь, ведет к увеличению популяции добычи и т. д.

Р ассмотрим отдельные значения г = 0,001, а = 2 * 10 ^–6; s = 0,01; b=10 ^-6, исходные разме­ры популяций составляют х(0) = 12 000 и y(0) = 600. На рис. представлено числен­ное решение уравнений (1) и (2), полученное при использовании вычислительного пакета, разработанного для численного решения систем дифференциальных уравнений (а не языка непрерывного моделирования).

Обратите внимание на то, что приведенный выше пример полностью детерми­нистический, то есть в нем нет случайных компонентов. Однако имитационная модель может содержать и неизвестные величины; например, в уравнения (1) и (2) могут быть добавлены случайные величины, которые каким-то образом за­висят от времени, или постоянные множители могут быть смоделированы как ве­личины, случайно изменяющие свои значения в определенные моменты времени.

Вопрос 17

Комбинированное непрерывно-дискретное моделирование

Поскольку некоторые из систем невозможно отнести ни к полностью дискретным, ни к полностью непрерывным, может возникнуть необходимость в создании моде­ли, которая объединяет в себе аспекты как дискретно-событийного, так и непре­рывного моделирования, в результате чего получается комбинированное непрерыв­но- дискретное моделирование. Между дискретным и непрерывным изменениями переменных состояния могут происходить три основных типа взаимодействия:

- дискретное событие может вызвать дискретное изменение в значении не­прерывной переменной состояния;

- в определенный момент времени дискретное событие может вызвать изме­нение отношения, управляющего непрерывной переменной состояния;

- непрерывная переменная состояния, достигшая порогового значения, мо­жет вызвать возникновение или планирование дискретного события.

В следующем примере комбинированного непрерывно-дискретного моделиро­вания дано краткое описание модели, подробно рассмотренной Прицкером, который в своей работе приводит и другие примеры этого типа моделирования.

Пример

Танкеры, перевозящие нефть, прибывают в один разгрузочный док, попол­няя резервуар-хранилище, из которого нефть по трубопроводу попадает на нефтепере­гонный завод. Из разгружающегося танкера нефть подается в резервуар-хранилище с по­стоянной скоростью (Танкеры, прибывающие к занятому доку, образуют очередь.) На нефтеперегонный завод нефть подается из резервуара с различными заданными скорос­тями. Док открыт с 6.00 до 24.00. По соображениям безопасности разгрузка танкеров прекращается по закрытии дока.

Дискретными событиями в этой (упрощенной) модели являются прибытие танкера на разгрузку, закрытие дока в полночь и открытие в 6.00. Уровни нефти в разгружающемся танкере и резервуаре-хранилище задаются переменными непрерывного состояния, ско­рости изменения которых описаны с помощью дифференциальных уравнений. Разгрузка танкера считается завершенной, когда уровень нефти в тан­кере составляет менее 5 % его емкости, но разгрузка должна быть временно прекращена, если уровень нефти в резервуаре-хранилище станет равным его емкости. Разгрузка мо­жет быть возобновлена, когда уровень нефти в резервуаре станет меньше 80 % его емко­сти. В случае если уровень нефти в резервуаре станет меньше 5000 баррелей, нефтепере­гонный завод должен быть временно закрыт. Для того чтобы избежать частого закрытия и возобновления работы завода, подача нефти из резервуара на завод не будет возобнов­ляться до тех пор, пока в нем не наберется 50 000 баррелей нефти. Каждое из пяти собы­тий, связанных с уровнем нефти (например, падение уровня нефти ниже 5 % емкости танкера), по определению Прицкера, является событием состояния. В отличие от диск­ретных событий, события состояния не планируются, они происходят, когда перемен­ные непрерывного состояния переходят пороговое значение.

18. Этапы разработки имитационных моделей

Практика разработки имитационных моделей реальных систем позволила выделить следующие этапы этого процесса.

1. Определение системы - установление границ, ограничений и критериев эффективности изучаемой системы.

2. Формулирование модели - переход от реальной системы к некоторой логической схеме.

3. Подготовка данных - отбор данных, необходимых для построения модели и представления их в соответствующей форме.

4. Разработка программного обеспечения — описание модели на языке, приемлемом для используемого компьютера.

5. Оценка адекватности - оценка соответствия результатов функционирования реальной системы и результатов, получаемых на основе имитационной модели.

6. Стратегическое планирование - планирование эксперимен­та для получения необходимой информации с наименьшими затра­тами средств.

7. Тактическое планирование - определение способа проведе­ния каждой серии испытаний, предусмотренных планом экспе­римента.

8. Экспериментирование - имитация процесса на компьютере для получения необходимой информации об исследуемой системе и анализа чувствительности модели.

9. Интерпретация - формулировка выводов и рекомендаций по результатам проведенных исследований.

10. Реализация - практическое использование модели и резуль­татов моделирования.

11. Документирование - регистрация хода осуществления про­екта и использования его результатов.

В связи с тем что перечисленные этапы ИМ определены, воз­можно, не самым эффективным способом, задача создания" мето­дологии ИМ до настоящего времени окончательно не решена.

19. Системный подход к формированию имитационных моделей

При исследовании и особенно при формировании сложных систем в любой сфере человеческой деятельности в последнее время большое распространение получил методологический под­ход, называемый системным. Рассмотрение объекта исследования в многообразии его связей с другими объектами и его построение в целях повышения эффективности большой системы можно назвать системным подходом. Под большой системой понимают систему, частью которой является изучаемый объект. Системный подход предполагает комплексный учет взаимодействия всех элементов системы.

В современных представлениях понятие системы имеет важное значение. В настоящее время системный подход для решения сложных задач получил достаточно широкое распространение. Использование этого подхода обусловлено тем, что если даже ка­ждый элемент или подсистема имеет оптимальные конструктив­ные или функциональные характеристики, то результирующее поведение системы в целом вследствие взаимодействия между ее отдельными частями может оказаться субоптимальным.

А. Эйнштейн как-то сказал, что «правильная постановка задачи более важна, чем ее решение». Чтобы найти приемлемое или оп­тимальное решение задачи, вначале необходимо знать, в чем она состоит.

Во многих случаях заказчик имитационной модели не может точно сформулировать свою проблему. Поэтому анализ системы обычно начинается с ее изучения, причем опыт показывает, что постановка задачи является, непрерывным процессом в течение всего хода исследования. Это связано с непрерывным получением новой информации, касающейся ограничений, задач я возможных альтернативных вариантов. В целях уточнения формулировки и постановки задачи такую информацию необходимо периодически использовать.

Важной частью постановки задачи является нахождение харак­теристик изучаемой системы. Поскольку все системы представляю собой подсистемы более крупных систем, первый шаг при решении этой задачи состоит в проведении анализа той срёды,

в которой находится система. Этот анализ начинается с определе­ния целей и граничных условий (т. е. того, что является и не явля­ется частью системы). При этом необходим учет существенных связей, имеющихся между изучаемой системой и окружающей средой, в которой она функционирует.

Определив задачи исследования и границы системы, следует составить ее логическую структурную схему, или так называемую статическую модель. Требуется построить такую модель системы, которая, с одной стороны, не будет настолько упрощенной, что станет тривиальной_, а с другой - не будет настолько детализиро- ванной, что станет громоздкой в обращении и чрезмерно дорогой. При этом ситуация осложняется тем, что усовершенствование модели характеризуется увеличением количества параметров, ко­торые иногда ничего не вносят в понимание рассматриваемой задачи.

Системные аналитики слишком часто стремились отразить все сложности реальных систем в модели, надеясь, что с помощью компьютера они решат все проблемы. Такой подход нецелесообра­зен не только потому, что при его использовании осложняется программирование и возрастает стоимость прогонов, но и потому, что действительно важные аспекты и взаимосвязи между ними могут оказаться неучтенными. Во избежание этого следует строить модель, ориентированную на решение конкретных задач, а не ими­тировать подробно реальную систему. Закон Парето гласит, что в каждой группе или совокупности существует жизненно важное меньшинство м тривиальное большинство. В связи с этим модель должна отображать только те аспекты системы, которые могут оказать существенное влияние на достижение желаемых резуль­татов.

20. Основные свойства систем, являющиеся причиной возникновения ошибок при попытки улучшить поведение системы.

Сложные системы отличаются свойствами, являющимися причиной возникновения многих ошибок при попытке улучшить поведение системы. Отметим среди них следующие.

1. Изменчивость. Характеристики системы изменяются, по­скольку в процессе эволюционного развития те или иные элементы вводятся в состав системы или выводятся из него.

2. Наличие окружающей среды. Каждая система существует в окружающей ее среде и является подсистемой более крупной сис­темы. Окружающая систему среда представляет собой комплекс элементов с определенными свойствами, которые хотя и являются

частью системы, однако при их модификации могут вызвать изме­нения состояния системы. Поэтому окружающая систему среда должна быть описана всеми внешними переменными, которые могут оказать влияние на систему.

3. Противоинтуитивное поведение. Поверхностное ознаком­ление со сложными системами может привести к выводу о необ­ходимости того или иного корректирующего воздействия, однако оно бывает неэффективным или даже приводит к обратным ре­зультатам. Причины и следствия часто не имеют тесной связи во времени и пространстве, признаки следствия могут проявиться намного позже начала действия вызвавших их причин. Очевидные решения в действительности могут привести к осложнению про­блемы, а не к ее решению.

4. Тенденция к ухудшению характеристик. Характеристики слож­ных систем, как правило, с течением времени ухудшаются. На­пример, части, из которых состоит система, изнашиваются, это становится одной из причин снижения эффективности ее функ- ционировакия, что может привести к негативным последствиям в ходе принятия проектных решений.

5. Взаимозависимость. Каждое событие в сложной системе за­висит от предшествующих событий и оказывает влияние на после­дующие. Кроме того, различные процессы в реальных условиях протекают параллельно и в конечном счете оказывают влияние друг на друга.

6. Организация. Сложные системы состоят из элементов, ха­рактеризующихся высокой степенью организации. Части объеди­няются в иерархии подсистем, которые взаимодействуют между собой для выполнения целевого назначения системы. Следует отметить, что выбор элементов, вводимых в систему или выводи­мых из нее, и их конфигурация определяются исследователем. В связи с этим при определении понятия изучаемой системы и гра­ниц между нею и окружающей ее средой следует проявлять боль­шую осторожность.

21. Основные три задачи, решаемы при имитационном моделировании

Прежде чем, переходить к разработке имитационной модели, необходимо понять, что собой представляют элементы, из которых она строится. Несмотря на то, что математическая или физическая структура модели может быть очень сложной, основы ее построе­ния весьма просты. В общем случае изучаемую систему можно охарактеризовать векторами входных, внутренних и выходных па­раметров , , , соответственно, причем -i-мерное эвклидово арифметическое пространство. Выходные парамет­ры, как правило, называют характеристиками. Одни и те же физи­ческие, экономические или информационные характеристики в моделях различного уровня и содержания могут выполнить функ­цию как внешних или внутренних, так и выходных параметров. Тогда структуру имитационной модели можно представить в виде у = f(x, z), где f- векторная функция векторного аргумента. Ис­пользование такой модели позволяет легко определять выходные параметрs по задаваемым значениям входных и внутренних па­раметров, т. е. решать так называемую прямую задачу. В инженер­ной практике решение такой задачи часто именуют поверочным расчетом.

При разработке системы возникает необходимость решать бо­лее сложную обратную задачу, или задачу управления: по задан­ному математическому описанию системы и известным выходным параметрам найти входные параметры. Решение обратной задачи осуществляют с помощью проектировочного расчета, цель которо­го часто состоит в определении входных параметров по некоторо­му критерию оптимизации W = W(x,y,z). Для такого расчета необ­ходимо ввести ограничения на области существования компонент вектора х, а также функциональные ограничения, связывающие компоненты векторов хиг.

Гораздо более сложная обратная задача возникает, когда за­даны совокупности входных и выходных параметров и необхо­димо составить математическое описание самой системы. Эта задача известна как задача идентификации, или структурного синтеза, системы. Трудность в этом случае состоит в том, что одно и то же соотношение между входными и выходными па­раметрами может описываться различными математическими вы­ражениями.

Задача идентификации может быть решена на основе принципа «черного ящика» путем математической обработки информации, полученной с помощью соотношений между входными и выход­ными параметрами, установленных в ходе проведения экспери­мента. Один из способов решения такой задачи состоит в примене­нии регрессионного анализа.

Прямая задача - когда определяются выходные параметры по заданным входным и внутренним параметрам.

Обратная задача (задача управления) – когда по заданному математическому описанию системы и известным выходным параметрам находят выходные параметры.

Задача идентификации (задача типа «черный ящик») -наиболее сложная из 3-х перечисленных, заданы совокупности входных и выходных параметров нужно произвести математическое описание самой системы.

22. Методы, используемые при построении и проверке имитационных моделей

В целом имитационная модель предназначена отражать струк­туру и внутренние связи моделируемой системы. Правильность построения модели может быть проверена только на практике. Так как при создании любой модели используют упрощения и абст­ракции реальной системы, модель не может быть абсолютно точ­ной в отношении однозначного ее соответствия реальной системе. Имитационное моделирование проводят не с целью поиска абсо­лютной истины, с его помощью можно лишь получить множество последовательных приближений к абсолютно точным данным. Проблема обоснования применимости имитационной модели ни­чем не отличается от аналогичной проблемы, касающейся теории или гипотезы в любой отрасли науки.

Поскольку построение модели и ее проверка являются неотъ­емлемыми элементами любой теории научных исследований, рассмотрим вкратце некоторые методы таких исследований.

Субъективные и объективные методы. При построении и обосновании имитационных моделей часто возникает противо­речие между стремлением к объективности и необходимостью использовать субъективные представления. Под этими пред­ставлениями понимают взгляды, интуицию, мнения, ощущения, предположения и впечатления, которые имеются относительно того, как работает изучаемая система. Под объективными пони­мают представления, основанные только на экспериментальных данных. Это противоречие можно разрешить, если процесс по­строения модели рассматривать как непрерывные дополняющие друг друга переходы от субъективных соображений к объектив­ным фактам и наоборот.

Рационализм и эмпиризм. Представители этих направлений единодушны во мнении о том, что наука начинается с наблюдений над некоторым объектом или процессом, но на этом их взаимопо­нимание заканчивается.

Рационалисты делают свои выводы на основе математики и логики. Их деятельность обычно направлена на разработку мате­матически выражаемых гипотез относительно взаимодействий сис­темы, причем таких, которые отвечают данным имеющихся на­блюдений, а затем - на применение методов формальной логики для получения тех или иных результатов. Однако, как правило, вскоре выявляется неточность принимаемых допущений и предпо­сылок, на которых основаны конкретные модели.

Так, известна модель развития городов, базирующаяся на предпосылках, которые содержат обоснование в собственной формулировке. Однако главное предположение о том. что, если на душу населения тратится больше собранных в виде налогов средств, качество обслуживания населения улучшается, не оче­видно, а в условиях современных городов не выдерживает ни­какой критики.

Эмпиризм отражает противоположное направление. Эмпирик отказывается принимать любые предпосылки или допущения, ко­торые не могут быть проверены с помощью эксперимента или на основе анализа эмпирических данных. Иными словами, эмпиризм основывается на доказанных фактах и отказе от непроверенных предположений.

Абсолютный прагматизм. Если имитационную модель рас­сматривать как «черный ящик», преобразующий входные пере­менные в выходные, рационалист и эмпирик занимаются опреде­лением структуры этого «ящика». Прагматика совершенно не интересует его структура, он занят лишь исследованиями соотно­шений между входом и выходом. При таком подходе упомянутая выше модель, основанная на связи экономических циклов с пятна­ми на Солнце, должна быть принята, если она дает лучшие резуль­таты, чем другие модели.

Утилитарный подход. Рационалисты, эмпирики и прагматики, придерживающиеся только одного направления, встречаются очень редко. Большинство экспериментаторов обычно в той или иной степени используют все эти методы, и такой подход можно назвать утилитарным. На первой стадии решение задач моделиро­вания сводится к построению внутренней структуры модели на основе априорной информации предыдущих исследований и су­ществующих теорий. Любая сложная имитационная модель состо­ит из множества простых моделей. Имитируемые этими моделями процессы обычно очевидны и понятны. Однако при их объедине­нии в сложную систему большое количество вариантов возмож­ных взаимодействий делает понимание поведения всей этой сис­темы затруднительным.

23. Стадии построения модели

Рассмотрим стадии построения модели.

Первая стадия состоит в рассмотрении и моделировании про­стых составляющих сложной системы. При таком подходе нет необходимости в эмпирической проверке каждой гипотезы, но требуется, чтобы каждая используемая гипотеза была основана на полных знаниях об изучаемой системе. Таким образом, на первой стадии применяется рационалистический подход, при котором не принимаются синтетические априорные допущения Канта, а необходимо лишь, чтобы допущения имели физический смысл.

Вторая стадия также связана с построением внутренней струк­туры модели и состоит в эмпирической проверке (когда это воз­можно) используемой гипотезы. Основой для такой оценки и про­верки гипотез может быть теория математической статистики.

Третья стадия состоит во всесторонней проверке пригодности модели для предсказания поведения реальной системы, заклю­чающейся в проверке соотношений входных и выходных парамет­ров. При этом лучшей считается модель, которая наиболее точно предсказывает поведение системы.

Рассмотренные три стадии при создании модели осуществля­ются итеративно, в процессе их проведения учитываются точки зрения рационалиста, эмпирика и прагматика. При построении и применений модели необходимо помнить о возможности возник­новения на всех стадиях различного рода ошибок и делать все воз­можное, чтобы их избежать.

Итак, процесс построения и проверки модели состоит из трех стадий:

- использование ряда гипотез о способах взаимодействия эле­ментов сложной системы, основанных на имеющейся информации, которая включает наблюдения, результаты предыдущих исследо­ваний, теории и интуитивные представления;

- проверка (когда это возможно) принятых допущений и гипо­тез с помощью статистических тестов;

- сравнение соотношений входных и выходных параметров модели и реальной системы.

24. Задачи и цели имитационного моделирования

В процессе создания имитационной модели, по крайней мере, необходимо определить следующее:

• назначение модели;

• какие элементы должны входить в модель;

• параметры включенных элементов;

• функциональные соотношения между элементами и описы­вающими их параметрами.

Эксперименты по моделированию проводят с различными це­лями, из которых наиболее распространенными являются:

оценка - определение, в какой степени предлагаемая структу­ра системы будет отвечать некоторым конкретным критериям;

сравнение - сопоставление систем, предназначенных для вы­полнения определенной функции, или сопоставление нескольких предлагаемых принципов или методов;

прогноз - предсказание поведения системы при некотором предполагаемом соотношении рабочих параметров с учетом ус­ловий эксплуатации;

анализ чувствительности - выявление из большого числа факторов и параметров тех. которые в наибольшей степени влияют на поведение системы в целом;

оптимизация - точное нахождение такого соотношения па­раметров, при котором обеспечивается наилучший отклик (крите­рий оптимизации) всей системы в целом;

выявление функциональных соотношений - определение зави­симости между двумя или несколькими параметрами и откликом системы.

Четкая формулировка цели построения модели имеет сущест­венное значение при ее создании и экспериментальной проверке. Например, если модель предназначена для того, чтобы определить характеристики проектируемой или существующей системы, то это отражается на ее точности; при этом требуется высокая сте­пень изоморфизма модели. В то же время, если назначением моде­ли является лишь сравнительная оценка двух или нескольких сис­тем или рабочих параметров, модель может быть пригодна даже в том случае, если абсолютное значение ее отклика на внешние воз­действия существенно отличается от соответствующего значения в реальной системе.

25. Проверка модели. Основные способы проверки.

Рассмотрим вопросы, связанные с проверкой модели, в ходе которой достигается приемлемый уровень уверенности пользова­теля в том, что любой вывод о поведении системы, сделанный на основе моделирования, будет верным.

Проверка модели - это чрезвычайно важный процесс, который должен выполняться непрерывно. Тем не менее необходимо выде­лить два наиболее важных этапа при проведении проверки. Пер­вый этап связан с созданием имитационной модели и состоит в проверке математической модели со всеми ее допущениями, назы­ваемой концептуальной. На втором этапе осуществляется проверка имитационной модели в целом.

Рассмотрим такие важные термины, использующиеся при моде­лировании, как «верификация», «валидация» и «доверие к модели».

При верификации - проверке достоверности модели, определя­ется, правильно ли по концептуальной модели составлена компью­терная программа, т. е. выполняется отладка моделирующей про­граммы.

Приведем несколько методов верификации компьютерных программ, представляющих интерес при отладке работы имита­ционной модели. Одни из этих методов применимы к любым компьютерным программам, другие же предназначены исклю­чительно для ИМ.

При разработке имитационной модели компьютерную про­грамму лучше писать и отлаживать по модулям или подпрограм­мам. В процессе разработки сложных имитационных моделей же­лательно, чтобы компьютерную программу проверяли несколько человек, так как разработчик может слишком привыкнуть к своей программе и не заметить ошибок. В некоторых организациях этот подход осуществляют на практике, он называется структурным разбором. Иногда, чтобы убедиться, что получены удовлетворительные результаты, достаточно выполнить прогон имитационной модели с различными входными параметрами. В некоторых случаях можно точно вычислить простые рабочие параметры и использовать их для сравнения. Одним из наиболее распространенных методов, применяемых для отладки дискретно-событийных имитационных программ, явля­ется трассировка. При ее проведении данные о состоянии модели­руемой системы, т. е. список событий, переменные состояния и др., выводятся на экран после возникновения каждого события и срав­ниваются с результатами вычислений. При трассировке желательно оценить все возможные ветви программ, а также возможность обрабатывать предельные условия функциони­рования системы.

Валидация - это процесс, использование которого дает воз­можность установить, является ли имитационная модель (не ком­пьютерная программа) точным представлением системы для кон­кретных целей исследования. Валидацию можно противопоставить интерпретации или ана­лизу выходных данных (см гл. 6), который представляет собой статистическую задачу, связанную с оценкой достоверности ре­зультатов, полученных с помощью имитационной модели. При анализе выходных данных необходимо знать продолжительность прогона и переходного периода, а также число независимых про­гонов имитационной модели.

26. Имитационная модель реальной системы, факторы и предпосылки для её создания

Математическая модель, которую требуется изучить путем моделирования называют имитационная модель.

Оценивая целесообразность применения метода ИМ для иссле­дования конкретной системы, необходимо учитывать его очевид­ные достоинства и недостатки. Имитационное моделирование, как правило, используют в случаях, когда:

• не существует адекватной математической постановки либо не разработаны аналитические методы решения сформулирован­ной математической модели (например, модели массового обслу­живания, модели для решения военно-технических задач и др.);

• аналитические методы имеются, но математические операции настолько сложны и трудоемки, что ИМ позволяет решить задачу с меньшими затратами ресурсов;

-из-за слабой подготовки технического персонала использо­вать имеющиеся аналитические решения невозможно;

• представляет интерес наблюдение за ходом процесса во вре­мени, а не только оценка выходных характеристик;

-ИМ оказывается единственной возможностью исследований из-за трудностей, возникающих при постановке экспериментов и наблюдениях за проведением процесса в реальных условиях (кос­мос, стратегические оборонные инициативы и др.);

• имеется возможность сжатия временной шкалы исследуемого процесса (анализ старения городов).

Дополнительным преимуществом ИМ можно считать широкие возможности его применения в сфере образования и профессио­нальной подготовки. Разработка и использование имитационной модели позволяют экспериментатору исследовать на модели ре­альные процессы и ситуации. Это, в свою очередь, в значительной мере способствует более глубокому пониманию проблемы, что стимулирует процесс поиска нововведений.

В силу своей простоты идея ИМ интуитивно привлекательна как для руководителей, так и для исследователей систем. Поэтому метод ИМ стремятся применять для решения каждой задачи, с которой приходится сталкиваться. И хотя специалистам с высоким уровнем математической подготовки ИМ представляется последним средст­вом, к которому следует прибегать, этот метод является самым рас­пространенным при решении проблем управления; доля использо­вания ИМ из всех методов исследования операций - свыше 30 %.

Однако, как и другие методы, (ИМ имеет недостатки, ограничи­вающие сферу его применения:

-разработка имитационной модели часто обходится дорого, поскольку для этого требуется много времени, а также наличие высококвалифицированных специалистов;

-из-за трудностей получения исходной статистической ин­формации Имитационная модель не всегда отражает действи­тельность;

-трудность оценки точности результатов, однако эта про­блема свойственна всем типам моделей;

• с помощью модели, как правило, можно получить только результаты в численном виде.

Анализ достоинств и недостатков показывает, что, 'хотя ИМ яв­ляется чрезвычайно ценным и полезным методом решения слож­ных задач, этот метод, конечно, не панацея для преодоления всех трудностей в процессе исследования. Разработками применение ИМ в большей степени является искусством, чем наукой. Неудача определяется не столько методом, сколько тем, как он используется.

Для успешного применения разрабатываемой имитационной модели и она должна отвечать следующим требованиям:

• целенаправленность;

• адекватность описываемым процессам;

• точность, обеспечивающая приемлемое совпадение реальных выходных данных и данных, полученных с помощью модели;

-полнота в отношении учета всех интересующих особенно­стей функционирования системы;

-простота, наглядность и доступность для понимания поль­зователем;

• удобство в управлении и обращении;

• адаптивность к изменению исходных данных;

робастность, характеризующая устойчивость модели по от­ношению к погрешности исходных данных.

В процессе создания имитационной модели, по крайней мере, необходимо определить следующее:

• назначение модели;

• какие элементы должны входить в модель;

• параметры включенных элементов;

• функциональные соотношения между элементами и описы­вающими их параметрами.

Эксперименты по моделированию проводят с различными це­лями, из которых наиболее распространенными являются:

» оценка - определение, в какой степени предлагаемая структу­ра системы будет отвечать некоторым конкретным критериям;

• сравнение - сопоставление систем, предназначенных для вы­полнения определенной функции, или сопоставление нескольких предлагаемых принципов или методов;

• прогноз - предсказание поведения системы при некотором предполагаемом соотношении рабочих параметров с учетом ус­ловий эксплуатации;

• анализ чувствительности - выявление из большого числа факторов и параметров тех. которые в наибольшей степени влияют на поведение системы в целом;

»оптимизация - точное нахождение такого соотношения па­раметров, при котором обеспечивается наилучший отклик (крите­рий оптимизации) всей системы в целом;

• выявление функциональных соотношений - определение зави­симости между двумя или несколькими параметрами и откликом системы.

27. Схемы образования случайных величин. Три типа физической природы возникновения случайных величин.

При создании имитационных моделей приходится сталкивать­ся с различными случайными величинами, процессами и события­ми. Случайными являются результаты отдельных выстрелов, мо­менты, в которые они были произведены, взаимное расположение снаряда и цели во время выстрела и т. д. В связи с производствен­ными допусками, кроме того, случайными будут скорость и даль­ность полета снарядов, а также эффективность действия боевой части. Случайным будет и сочетание географических, климатиче­ских и метеорологических условий боя, Это перечисление можно продолжить для моделей массового обслуживания, экономическо­го и социального развития и т. п.

Законы распределения случайных величин являются отражени­ем физической природы возникновения этих величин, и поэтому выбор математического выражения для описаний статистических свойств тех или иных явлений не может быть произвольным. Можно выделить три типа явлений, встречающихся на практике.

К первому типу следует отнести явления очень сложной физи­ческой природы, для которых не представляется возможным про­гнозировать характер статистических закономерностей. В таких случаях проводится накопление статистических данных, а затем осуществляется формальный подбор математического выражения, при использовании которого вероятностные свойства эмпириче­ского распределения описываются удовлетворительно. Например, существует система кривых распределения Пирсона и разработан специальный математический аппарат для выбора типа кривой, обеспечивающей совпадение первых четырех моментов теоретиче­ского и эмпирического распределений.

Следует отметить, что, хотя такой формальный подход в целом позволяет достичь удовлетворительного описания эксперименталь­ных данных, иногда его применение приводит к нарушению физи­ческого смысла в некотором интервале значений случайной вели­чины. Нередки случаи, когда распределение случайной величины, заведомо являющейся положительной, аппроксимируется нормаль­ным законом, что приводит к абсурдному результату: cp(.x) > 0 при v <0 В основном такие несоответствия носят чисто формальный характер и не отражаются на практической стороне дела, посколь­ку вероятность появления абсурдных значений случайной величи­ны мала. Тем не менее необходимо стремиться к получению тако­го описания экспериментальных данных, при котором для всего диапазона изменения случайной величины сохранялся бы физиче­ский смысл

Ко второму типу можно отнести явления, которые допускают хотя бы схематическое описание механизма получения случайной величины, что дает возможность логического (может быть, не стро­гого математически) выбора закона распределения для описания их статистических свойств. Такого рода физически обоснованные законы распределения имеют большую практическую ценность, в отличие от вариантов, базирующихся на чисто формальном подборе математических соотношений, им должно отдаваться предпочтение.

К третьему типу следует отнести хорошо изученные явления, для которых можно провести строгое обоснование вида закона распределения случайной величины.

Изложенное объясняет то, что для описания событий исследо­ватели используют различные законы распределения, нередко ока­зывающиеся удовлетворительными только для частных случаев

Далее приведены основные схемы случайных явлений, для ко­торых возможно использование наиболее распространенных зако­нов распределения Рассмотрим в первую очередь наиболее часто встречающиеся на практике распределения дискретных случайных величин.

Бывают следующие виды распределения:

Биномиальное распределение Имеется п независимых случай­ных величин Х_и Л';, .., Х„, которые могут принимать значение 1 с вероятностью р и значение 0 с вероятностью q ~ (1 -р).

Распределение Пуассона. Основная схема, которая приводит к этому распределению, состоит в следующем. Предположим, что на некоторой оси распределены точки, при этом ось можно использо­вать для отсчета времени, площади, расстояния и т. д. Точки же означают случаи того, что интересующее нас событие произошло. Задача состоит в том, чтобы определить закон распределения чис­ла точек на участке оси длиной /, Это может быть число целей, расположенных в заданном интервале боевого порядка, число вы­стрелов, произведенных за время t, число осколков, попавших в уязвимую площадь цели, и г. д.

Геометрическое распределение. Это распределение является дискретным аналогом экспоненциального распределения, рассмат­риваемого в дальнейшем, в том отношении, что это единственное дискретное распределение с отсутствием последействия.

Равномерное распределение. Случайная величина имеет рав­номерное распределение на отрезке [а, Ь], если ее плотность рас­пределения имеет вид

Нормальное распределение. Нормальный закон распределения в качестве предельного можно получить из биномиального закона и закона Пуассона. Однако наиболее общая схема, приводящая к этому закону и показывающая причины его широкого распро­странения, следует из центральной предельной теоремы теории вероятностей. Эта теорема утверждает, что в общем случае сумма независимых случайных величин с произвольными законами рас­пределения асимптотически нормальна. Когда среди случайных величин нет доминирующей (все слагаемые вносят в сумму при­мерно одинаковый вклад), суммарный закон распределения ста­новится приблизительно нормальным уже при числе слагаемых, равном 3-5.

Экспоненциальное {показательное) распределение. При рас­смотрении схемы, приводящей к закону Пуассона, можно устано­вить закон распределения, которому подчиняются длины «пустых» (не содержащих точек) интервалов оси. Обозначим случайный промежуток времени между событиями Т. Тогда интегральный закон распределения можно представить следующим образом: F(t) = P(T<t) = 1-Р(Т>1) = 1-е^-λt где P(T>t) = Р₀(t) = е^-λt - веро­ятность того, что на промежутке времени t не произойдет ни одно­го события, причем 0 ≤ t ≤ ∞.

Следовательно, функция плотности распределения длины «пус­тых» интервалов будет иметь вид

f(t) =λ е^-λt

Вопрос 28

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятность. ,

где Х – случайная величина, - значения, вероятности которых соответственно равны .

Математическое ожидание приближённо равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания: .

Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии: .

Дискретное распределение (общий случай). Предположим, что известны частоты а_i выбора из N объектов на определенном интервале времени, i=1,....,N. Пример таких частот для N =7 представлен в табл. 1. Первая строка таблицы - это номер объекта, а вторая -частота его выбора. Требуется разработать программную функцию, которая должна возвращать значение номера объекта в соответствии с этими частотами.

Значения обратных функций для получения дискретного распределения

В оспользуемся методом обратных функций. Сначала найдем сумму всех частот:

В нашем случае получаем =291. После этого построим таблицу нормированных значений _i=_i/(третья строка табл. 1.3). Далее рассчитаем значения дискретной функции _i; по формуле

Значения _i находятся в четвертой строке табл. 1.3. Построим график дискретной функции у, Далее воспользуемся рассмотренной выше программой получения случайных величин, распределенных равномерно на отрезке (0,1), и каждый раз будем получать случайную величину р,. Условимся, что То = 0 . По­сле этого выбор объекта с номером i осуществляется при выполне­нии соотношения

Также для дискретных случайных величин существуют:

Биномиальное распределение, Геометрическое распределение, Гипергеометрическое распределение, Пуассоновское распределение

Вопрос 29 Непрерывные случайные величины.

Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.

В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полу­бесконечными или бесконечными, например: (a; b], (– ; a), [b;), (–; ).

Вообще непрерывная случайная величина – это абстракция. Снаряд, выпущенный из пушки, может пролететь любое расстояние, скажем, от 5 до 5,3 километров, но никому не придёт в голову измерять эту величину с точностью до 0,0000001 километра (то есть до миллиметра), не говоря уже об абсолютной точности. В практике такое расстояние будет дискретной случайной величиной, у которой одно значение от другого отличается по крайней мере на 1 метр.

При описании непрерывной случайной величины принципиально невозможно выписать и занумеровать все её значения, принадлежащие даже достаточно узкому интервалу. Эти значения образуют несчётное множество, называемое «континуум».

Если  – непрерывная случайная величина, то равенство  = х представляет собой, как и в случае дискретной случайной величины, некоторое случайное событие, но для непрерывной случайной величины это событие можно связать лишь с вероятностью, равной нулю, что однако не влечёт за собой невозможности события. Так, например, можно говорить, что только с вероятностью «нуль» снаряд пролетит 5245,7183 метра, или что отклонение действительного размера детали от номинального составит 0,001059 миллиметра. В этих случаях практически невозможно установить, произошло событие или нет, так как измерения величин проводятся с ограниченной точностью, и в качестве результата измерения можно фактически указать лишь границы более или менее узкого интервала, внутри которого находится измеренное значение.

Равномерное распределение на интервале (0,1).

Один из наиболее простых и эффективных вычислительных ме­тодов получения последовательности равномерно распределенных случайных чисел r_i, с помощью, например, калькулятора или любого другого устройства, работающего в десятичной системе счисления, включает только одну операцию умножения.

Описанная процедура в основном применяется для получения более сложных распределений, как дискретных, так и непрерывных. Эти распределения получаются с помощью двух основных приемов:

• обратных функций;

• комбинирования величин, распределенных по другим законам, например по равномерному на интервале (0,1).

Равномерное распределение на произвольном интервале. Рассмотрим важное и очень простое равномерное распределение на интервале (m-s, m+s). Плотность вероятностей этого распределения описывается следующей формулой:

где: m - математическое ожидание;

s - максимальное отклонение от математического ожидания

Такое распределение используется, если об интервалах времени известно только то, что они имеют максимальный разброс, и ничего не известно о распределениях вероятностей этих интервалов.

Нормальное распределение. Нормальное, или гауссово распре­деление, - это, несомненно, одно из наиболее важных и часто ис­пользуемых видов непрерывных распределений. Оно симметрично относительно математического ожидания. Сначала остановимся на практическом смысле этого распределения применительно к эконо­мическим задачам и сформулируем центральную предельную теорему теории вероятностей в следующей практической интерпретации.

Н епрерывная случайная величина t имеет нормальное распределение вероятностей с параметрами т и  > 0, если ее плотность вроятностей имеет вид:

где т - математическое ожидание M[t],

 - среднеквадратичное отклонение.

Причем если D[t} - это дисперсия, то = D[t] .

Практический смысл этой теоремы очень прост. Любые сложные работы на объектах экономики (ввод информации из документа в компьютер, проведение переговоров, ремонт оборудования и др.) состоят из многих коротких последовательных элементарных со­ставляющих работ. Причем количество этих составляющих работ иногда настолько велико, что требования в приведенной выше теореме о независимости и одинаковом распределении становятся из­лишними. Поэтому при оценках трудозатрат всегда справедливо предположение о том, что их продолжительность - это случайная величина, которая распределена по нормальному закону.

Экспоненциальное распределение. Оно также занимает очень важное место при проведении системного анализа экономической деятельности. Этому закону распределения подчиняются многие явления, например:

• время поступления заказа на предприятие;

• посещение покупателями магазина-супермаркета;

• телефонные разговоры;

• срок службы деталей и узлов в компьютере, установленном, например, в бухгалтерии.

Рассмотрим это распределение подробнее. Если вероятность на­ступления события на малом интервале времени Д< очень мала и не зависит от наступления других событий, то интервалы времени ме­жду последовательностями событий распределяются по экспоненци­альному закону с плотностью вероятностей

Особенностью этого распределения являются его параметры:

• математическое ожидание M[t] =1/.;

• дисперсия D[t]=²=(1/)².;

Математическое ожидание равно среднеквадратичному отклоне­нию, что является одним из основных свойств экспоненциального распределения

Обобщенное распределение Эрланга.

Обычно распределение Эрланга используется в случаях, когда длительность какого-либо процесса можно представить как сумму k элементарных последовательных составляющих, распределенных по экспоненциальному закону. Если обозначить математическое ожидание длительности всего процесса как M[t]= 1/, среднюю длительность элементарной составляющей как 1/, то плотность вероятностей распределения Эрланга представляется следующей формулой:

Дисперсия такого распределения D[t]=1/(²k)

Очевидно, что при k=1 - это экспоненциальное распределение. Разновидности этого распределения для разных k > 0 представлены на рис. 1.5.

Обобщенное распределение Эрланга применяется при создании как чисто математических, так и имитационных моделей в двух слу­чаях.

1) Его удобно применять вместо нормального распреде­ления, если модель можно свести к чисто математической задаче, применяя аппарат марковских или полумарковских процессов либо используя метод Кендалла. Однако такие модели далеко не всегда адекватны реальным процессам.

2) В реальной жизни существует объективная вероятность возникновения групп заявок в качестве реакции на какие-то действия, поэтому возникают групповые потоки. Применение чисто математических методов для исследования в моделях эффектов oi таких групповых потоков либо невозможно из-за отсутствия способа получения аналитического выражения, либо затруднено, так как ана­литические выражения содержат большую систематическую погреш­ность из-за многочисленных допущений, благодаря которым исследо­ватель смог получить эти выражения. Для описания одной из разно­видностей 1пуппового потока можно применить обобщенное распре­деление Эрланга, которое рассмотрим ниже. Внешне похожее на гам­ма-распределение, оно имеет свои математические особенности.

Появление групповых потоков в сложных экономических систе­мах приводит к резкому увеличению средних длительностей различ­ных задержек (заказов в очередях, задержек платежей и др.), а также к увеличению вероятностей рисковых событий или страховых случаев.

Треугольное распределение. Применимость такого распределе­ния связанно с динамическими характери­стиками системы управления базами данных (СУБД) в экономиче­ской информационной системой.

30. Выборочный метод Монте-Карло

В случаях, когда аналитические методы неприемлемы, исполь­зуют универсальный метод статистического моделирования, или, как его часто называют, метод Монте-Карло. Разыгрывание выборок по методу Монте-Карло является основ­ным принципом моделирования систем, включающих стохастиче­ские или вероятностные факторы. Его зарождение связано с работой Дж. фон Неймана и С. Улама в конце 1940-х годов, когда они ввели термин «Монте-Карло» и применили этот метод к решению некото­рых задач экранирования ядерных излучений. Этот термин был из­вестен уже много лет, но свое второе рождение он получил, когда нашел применение в Лос-Аламосе в закрытых работах по ядерной технике, которые велись под кодовым названием «Монте-Карло». Использование метода оказалось настолько успешным, что он полу­чил распространение и в других областях науки и техники; сегодня многим специалистам термин «метод Монте-Карло» представляется синонимом термина «имитационное моделирование». Несмотря на то что метод Монте-Карло целесообразно использовать при модели­ровании вероятностных ситуаций, он также применим и для реше­ния некоторых полностью детерминистских задач, не имеющих аналитического решения.

Метод Монте-Карло - это численный метод решения математи­ческих задач с использованием моделирования случайных чисел.

Суть метода проста и состоит в следующем: вместо того чтобы описывать случайное явление с помощью аналитических зависимо­стей, проводят «розыгрыш» - моделирование этого явления с полу­чением случайных результатов. При этом используют таблицы слу­чайных чисел, колесо рулетки, компьютерные подпрограммы и др. Проведя такой «розыгрыш» очень большое число раз, получают ста­тистический материал - множество реализаций случайного явления, - который затем обрабатывают методами математической статистики.

Метод Монте-Карло используют:

• при моделировании сложных процессов, на проведение кото­рых оказывает влияние множество различных случайных факторов;

• при оценке точности аналитических методов, основанных на определенных допущениях (например, пуассоновский характер потоков событий, независимость случайных величин, отсутствие накопления ущерба и т. д.);

• в целях выработки поправок к эмпирическим формулам.

31. Задачи, решаемые проведением розыгрыша

В сущности, методом Монте-Карло можно решить любую ве­роятностную задачу, но его использование становится целесооб­разным только тогда, когда проведение розыгрыша оказывается проще, а не сложнее получения аналитического решения.

Пример 1. По цели производят четыре независимых выстре­ла, каждый из которых попадает в нее с вероятностью р =0,5. Для поражения цели требуется не менее ю-2 попаданий. Необходимо определить вероятность поражения цели.

Аналитическое решение. Вероятность поражения Ж можно вы­числить через вероятность противоположного события - непора­жения цели, которое имеет место, если:

• не было ни одного попадания Р₀4 = 0,5⁴;

• было только одно попадание

Окончательно получаем:

Метод Монте-Карло. Пусть четыре выстрела - это четыре мо­неты; «орел» - попадание, «решка» - промах. Опыт, или розы­грыш, - это бросание четырех монет. Цель поражена, если при четырех бросаниях будет не менее двух «орлов»; опыт повторяется много раз. Тогда согласно теореме Бернулли частота поражения будет мало отличаться от вероятности этого события W. Пусть было N опытов, из них т раз цель была поражена. Следовательно, W=m/N= 0,688.

При решении этой задачи использование метода Монте-Карло сложнее получения аналитического решения.

Пример 2. По самолету снарядами производится стрельба так, что для поражения самолета необходимо, чтобы точки попа­дания располагались достаточно близко друг к другу. Требуется найти закон поражения, т. е. вероятность G{m) того, что самолет будет поражен, если в него попало m снарядов. Эту задачу проще решать розыгрышем, чем расчетом.

Пусть m=5. Найдем вероятность поражения самолета, если в него попали все снаряды. Разделим проекцию самолета на k эле­ментарных ячеек одинаковой площади, каждую из которых про­нумеруем. Изготовим k жетонов (тоже пронумеруем) и заложим их во вращающийся барабан.

Проведем опыт: будем вынимать из барабана пять жетонов по одному, каждый раз возвращая жетон в барабан и перемешивая жетоны.

Пусть всего проведено N опытов, в течение которых в п случа­ях было зарегистрировано поражение цели, т. е. жетоны оказались расположенными близко друг к другу.

Частота поражения цели:

Путем проведения розыгрыша можно определить не только ве­роятность интересующих нас случайных величин, но и математи­ческие ожидания и дисперсии. Основным элементом, из совокуп­ности которых создается статистическая модель, представляется одна случайная реализация моделируемого явления, например «один обстрел цели», «один день работы транспорта» и т. д.

Отдельную реализацию разыгрывают с помощью специально разработанного алгоритма, в котором важное значение имеет бро­сание жребия. Каждый раз, когда на ход явления оказывает влияние случай, это учитывается не расчетом, а жребием. Для реализации этого алгоритма необходимо использовать некоторый случайный механизм (например, бросить игральную кость или несколько мо­нет или выбрать число из таблицы случайных чисел и т. д.) и ус­ловиться о том, какой результат означает, что произошло некото­рое событие А, а какой - не означает. Такие механизмы могут быть различными, однако любой из них может быть заменен стандарт­ным механизмом, позволяющим решить одну-единственную задачу: получить случайную величину, распределенную с постоянной плот­ностью от 0 до 1, которую называют «случайное число от 0 до 1» и обозначают R или U.

Условимся называть единичным жребием любой опыт со слу­чайным исходом, проведение которого позволяет ответить на один из следующих вопросов.

1. Произошло событие А или нет? Пусть Р(А) = Р. С помощью стандартного механизма получим R (Приложение 2). Считаем, если R<P - событие произошло, а если R>P - событие не про­изошло.

2. Какое из событий А,, А₂, ..., А_к произошло? Имеется полная группа несовместных событий A_h А₂, ..., А„ с вероятностями P_t, Рг, Р_п, при этом Pi + Р> + ... + Р„ = \. Если R, полученное с по­мощью стандартного механизма, выпало на участок Р_и считаем, что событие А, произошло.

3. Какое значение приняла случайная величина Х. Пусть слу­чайная величина непрерывна и имеет заданную непрерывную функцию распределения F(x). Из рис. 2.24 следует, что при Х<х величина R< F(х), т. е. P(X<x)^P(R< F{x)). Если взять на оси ординат случайное число R (от О до 1) и найти значение X, при котором F(X) = R, то полученная случайная ве­личина X будет иметь функцию распре­деления F(x).

Следовательно, розыгрыш значения случайной величины X с заданной функцией распределения F (х) сводится к следующему:

• получить случайное число R (от 0 до 1),

• в качестве значения X использовать Х- F~^l{R), где F~^l - функция, обратная функции F.

При разработке имитационной модели, включающей стохасти­ческие или вероятностные элементы, всегда возникает вопрос: следует ли при использовании метода Монте-Карло применять эмпирические данные или же надо воспользоваться одним из тео­ретических распределений? Ответ на этот вопрос достаточно

прост: если есть возможность использо­вать теоретические распределения, мо­дель, как правило, получается лучше с учетом общности результатов и удобства ее применения.

В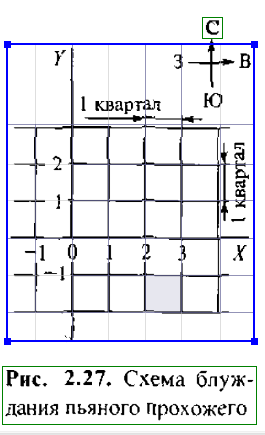 целях иллюстрации этого метода рассмотрим классическую задачу о пья­ном прохожем, которую также называют задачей о случайном блуждании. Пред­положим, что пьяный, стоя на углу ули­цы, решил прогуляться, чтобы развеять хмель. Пусть известны вероятности того, что, идя до очередного перекрестка, он пройдет на север, юг, восток или запад. Необходимо найти вероятность того, что, пройдя 10 кварталов, пьяный окажется не далее двух кварталов от места, от которого он начал прогулку. Схема блуждания пьяного прохожего приведена на рис. 2.27.

Начнем с того, что обозначим местоположение пьяного на ка­ждом перекрестке двухмерным вектором (A'. Y), где X - направле­ние с запада на восток, a Y - направление с юга на север. Каждое перемещение на один квартал к востоку соответствует увеличению А⁷ на 1, а каждое перемещение на один квартал к западу - умень­шению А' на 1 - Подобным же образом при передвижении пьяного на один квартал к северу Г увеличивается на 1, а на один квартал к югу - уменьшается на 1. Если обозначить начальное положе­ние (0, 0), то на каждом этапе прогулки можно точно знать, где находится пьяный относительно этого положения. В случае, если в конце прогулки протяженностью в 10 кварталов окажется, что сумма абсолютных значений X и Y больше 2, то, следовательно, пьяный ушел от начальной точки дальше, чем на два квартала. Разыгрывая случайные числа по схеме «какое событие произош­ло?» на каждом перекрестке, можно определить, где окажется пья­ный через 10 кварталов. Эти розыгрыши следует повторять необ­ходимое число раз, чтобы с достаточной степенью уверенности (с некоторой вероятностью) ответить на поставленный вопрос. В зависимости от различных привходящих обстоятельств можно изменять как вероятности выбора направления движения, так и цель пьяного блуждания.

Вопрос 32

Основные понятия математическая статистика

Математические законы теории вероятностей не являются бес­предметными абстракциями, не имеющими физического смысла; они представляют собой математическое выражение закономерно­стей, реально существующих в случайных массовых явлениях при­роды. Разработка методов регистрации, описания и анализа стати­стических экспериментальных данных, получаемых в результате наблюдений этих явлений, составляет предмет специальной науки - математической статистики.

Рассмотрим вкратце некоторые типичные задачи математиче­ской статистики, часто встречаемые на практике.

В реальных условиях всегда приходится оперировать с огра­ниченным количеством экспериментальных данных, в связи с чем результаты наблюдений и их обработка всегда в той или иной степени носят случайный характер. Возникает вопрос: ка­кие черты являются постоянными, а какие - случайными, встре­чающимися в конкретной серии наблюдений только из-за огра­ниченного объема экспериментальных данных? В связи с этим встает задача выравнивания статистических данных (регрессион­ный анализ).

Статистический материал может с большей или меньшей сте­пенью достоверности подтверждать справедливость той или иной гипотезы. Например, может возникнуть такой вопрос: согласуются ли результаты эксперимента с гипотезой о том, что данная случай­ная величина подчинена закону распределения f(x) (проверка ги­потез)? Кроме того, может появиться другой вопрос; указывает ли наблюдаемая в опыте тенденция к зависимости между двумя слу­чайными величинами на наличие действительной объективной зависимости между ними или же она объясняется случайными причинами, связанными с недостаточным объемом наблюдений (корреляционный анализу).

Зачастую приходится решать задачу определения некоторых параметров случайной величины на основе экспериментального материала. Это так называемая задача оценок искомых парамет­ров, т. е. нахождение таких их приближенных значений, использо­вание которых при массовом применении приводило бы в среднем к меньшим ошибкам (доверительный интервал и доверительная вероятность). Это далеко не полный перечень основных задач математической статистики.

Математическая (или теоретическая) статистика опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи.

В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей — свойства и взаимосвязи этих величин (распределений).

Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.

1. В математике сформировалась новая область — математическая статистика, изучающая общие закономерности статистических данных или явлений и взаимосвязи между ними.

Сфера применения математической статистики распространилась во многие, особенно экспериментальные, науки. Так появились экономическая статистика, медицинская статистика, биологическая статистика, статистическая физика и т.д. С появлением быстродействующих ЭВМ возможность применения математической статистики в различных сферах деятельности человека постоянно возрастает. Расширяется ее приложение и к области физической культуры и спорта. В связи с этим основные понятия, положения и некоторые методы математической статистики рассматриваются в курсе “Спортивная метрология”. Остановимся на некоторых основных понятиях математической статистики.

2. Статистические данные

В настоящее время под термином "статистические данные" понимают все собранные сведения, которые в дальнейшем подвергаются статистической обработке. В различной литературе их еще называют: переменные, варианты, величины, даты и т.д. Все статистические данные можно разделить на: качественные, труднодоступные для измерения (имеется, не имеется; больше, меньше; сильно, слабо; красный, черный; мужской, женский и т.д.), и количественные , которые можно измерить и представить в виде числа общих мер (2 кг, 3 м, 10 раз, 15 с и т.д.); точные , величина или качество которых не вызывают сомнений (в группе 6 человек, 5 столов, деревянный, металлический, мужской, женский и т.д.), и приближенные , величина или качество которых вызывает сомнение (все измерения: рост 170 см, вес 56 кг, результат бега на 100 м - 10,3 с и т.д.; близкие понятия — синий, голубой, мокрый, влажный и т.д.); определенные (детерминированные), причины появления, не появления или изменения которых известны (2 + 3 = 5, подброшенный вверх камень обязательно будет иметь вертикальную скорость, равную 0 и т.д.), и случайные , которые могут появляться и не появляться или не все причины изменения которых известны (пойдет дождь или нет, родится девочка или мальчик, команда выиграет или нет, в беге на 100 м — 12,2 с, принятая нагрузка вредна или нет). В большинстве случаев в физической культуре и спорте мы имеем дело с приближенными случайными данными.

3. Статистические признаки, совокупности

Общее свойство, присущее нескольким статистическим данным, называют их статистическим признаком . Например, рост игроков команды, результат бега на 100 м, принадлежность к виду спорта, частота сердечных сокращений и т.д.

Статистической совокупностью называют несколько статистических данных, объединенных в группу хотя бы одним статистическим признаком. Например, 7.50, 7.30, 7.21, 7.77 — результаты прыжка в длину в метрах у одного спортсмена; 10, 12, 15, 11, 11 — результаты подтягивания на перекладине пяти студентов и т.д. Число данных в статистической совокупности называют ее объемом и обозначают n . Различают следующие совокупности:

бесконечные — n (масса планет Вселенной, число молекул и т.д.); конечные — n - конечное число; большие — n > 30; малые — n 30;

генеральные — содержащие все данные, обусловленные постановкой задачи;

выборочные — части генеральных совокупностей.

Например, пусть рост студентов 17-22 лет в РФ — генеральная совокупность, тогда рост студентов КГАФК, всех студентов города Краснодара или студентов II курса — выборки.

4. Кривая нормального распределения

При анализе распределения результатов измерений всегда делают предположение о том распределении, которое имела бы выборка, если бы число измерений было очень большим. Такое распределение (очень большой выборки) называют распределением генеральной совокупности или теоретическим , а распределение экспериментального ряда измерений — эмпирическим.

Теоретическое распределение большинства результатов измерений описывается формулой нормального распределения, которая впервые была найдена английским математиком Муавром в 1733 г.:

5. Виды представления статистических данных

После того, как определена выборка и стали известны ее статистические данные (варианты, даты, элементы и т.д.), возникает необходимость представить эти данные в удобном для решения задачи виде. На практике используют много различных видов представления статистических данных. Наиболее часто употребляют следующие:

а) текстовый вид;

б) табличный вид;

в) вариационный ряд;

г) графический вид.

33. Программное обеспечение имитационного моделирования

При ИМ используют вычислительные системы трех типов - универсальные ЭВМ, электронные аналоговые машины и гибрид­ные ЭВМ. Преимущества каждой из них определяются специфи­кой основных свойств аналоговых и цифровых ЭВМ. Аналоговая вычислительная машина (АВМ) представляет переменные пара­метры в виде легкогенерируемых и управляемых физических ве­личин, например электрического напряжения. С ее помощью по­лучают решение, выполняя операции параллельно, в то время как цифровая ЭВМ производит операции последовательно (сериями). Это дает АВМ существенное преимущество в скорости вычисле­ний, особенно при решении систем дифференциальных уравнений.

В то же время цифровая ЭВМ может обеспечивать большую точность и расширенный функциональный диапазон в результате возможности считать, подчиняться логическим правилам, работать с плавающей точкой и использовать длинные слова. Таким обра­зом, одно из основных различий между АВМ и цифровыми ЭВМ заключается в способе обработки зависимых переменных. В АВМ для записи таких переменных (к независимым переменным это может и не относиться) используется непрерывная форма. В циф­ровых же ЭВМ все переменные (зависимые и независимые) пред­ставляются только в дискретном виде. Точность чисел (т. е. коли­чество значимых цифр) в АВМ ограничена качеством компонентов ее электрических цепей, в то время как точность цифровых ЭВМ зависит от количества разрядов и ограничена лишь размером или объемом регистров памяти.

В целом с любой задачей, которую решает АВМ, может спра­виться и мощная цифровая ЭВМ. Но на АВМ решать многие зада­чи можно быстрее, легче и дешевле.

При создании гибридных вычислительных систем сделана по­пытка объединить преимущества, присущие аналоговым и цифро­вым машинам, и устранить их недостатки. Некоторые типы задач обусловливают необходимость усовершенствовать цифровую ЭВМ добавлением аналоговой части для увеличения скорости расчетов. В то же время в аналоговых системах желательно обеспечить вы­сокую точность вычислений, гибкость, а также возможность как хранения данных, так и использования логических функций, ха­рактерных для цифровых ЭВМ.

Применение гибридных вычислительных систем в настоящее время, как правило, целесообразно, поскольку они позволяют уст­ранить недостатки, присущие как аналоговым, так и цифровым машинам. Однако по мере устранения этих недостатков преиму­щества гибридных ЭВМ при имитационном моделировании будут не столь очевидны. Например, уже в настоящее время большее быстродействие, меньшая стоимость, оперативный режим разде­ления времени в больших цифровых вычислительных системах значительно сузили диапазон применения гибридных систем.

При рассмотрении преимуществ и недостатков аналоговых, цифровых и гибридных вычислительных машин было установле­но, что для машинного ИМ можно использовать не только цифро­вую технику. При определенных обстоятельствах более предпоч­тительными могут оказаться аналоговые и гибридные машины. Желательно, чтобы исследователь имел возможность выбирать наиболее подходящую вычислительную машину. К сожалению, не каждый имеет доступ ко всем трем типам вычислительных машин, и на практике, вероятнее всего, используется та машина, которая имеется в распоряжении.

34. Особенности выбора программного обеспечения имитационного моделирования

При разработке имитационных моделей предъявляют опреде­ленные требования к функциональным возможностям, необходи­мым для программирования большинства дискретно-событийных моделей. К таким возможностям относятся:

• генерирование случайных величин с заданным распределени­ем вероятностей (например, с экспоненциальным распределением);

• продвижение часов модельного времени;

- определение каждого следующего события по списку со­бытий;

• добавление или удаление записей из списка;

-сбор и обработка выходных статистических данных и сос­тавление отчета с полученными результатами;

• определение сбойных ситуаций.

В сущности, именно эти и некоторые другие общие функцио­нальные возможности в моделирующих программах позволили разработать специальные программные пакеты ИМ. Более того, дальнейшее усовершенствование таких пакетов и простота их применения способствовали росту популярности ИМ в послед­ние годы.

Одно из наиболее важных решений, которые приходится при­нимать разработчикам моделей или аналитикам, касается выбора программного обеспечения (ПО). Если ПО недостаточно гибко или с ним сложно работать, то ИМ может дать неверные результа­ты или оказаться вообще невыполнимым.

Использование пакета DM по сравнению с применением уни­версального языка программирования имеет несколько преиму­ществ.

1. Пакеты ИМ автоматически предоставляют большинство функциональных возможностей, требующихся для создания имита­ционной модели, что позволяет существенно сократить время, необ­ходимое для программирования, и общую стоимость проекта.

2. Пакеты ИМ обеспечивают естественную среду для создания имитационных моделей. Их основные моделирующие конструк­ции больше подходят для имитационного моделирования, чем соответствующие конструкции в универсальных языках програм­мирования.

3. Имитационные модели, которые созданы с помощью паке­тов моделирования, как правило, проще модифицировать и ис­пользовать.

4. Пакеты ИМ обеспечивают более совершенные механизмы обнаружения ошибок, поскольку они выполняют автоматический поиск ошибок многих типов. И так как для использования модели не требуется большого числа структурных компонентов, вероят­ность совершить какую-либо ошибку снижается.

Тем не менее некоторые имитационные модели (особенно от­носящиеся к задачам оборонной сферы) по-прежнему создают с помощью универсальных языков программирования, которые так­же обладают некоторыми преимуществами.

1. .Языки программирования знает большинство разработчи­ков, чего нельзя сказать о пакетах ИМ.

2. Скорость выполнения прогона имитационных моделей, на­писанных на языках программирования, обычно больше, чем мо­делей, созданных с помощью пакетов имитационного моделиро­вания. Это связано с тем, что такие пакеты часто разрабатывают для различных систем посредством одного набора моделирующих конструкций, тогда как программа на языке программирования может быть более удачно написана для конкретной системы. Од­нако с распространением недорогих быстродействующих персо­нальных компьютеров это преимущество несколько утратило свою актуальность.

3.При программировании универсальные языки обеспечивают большую гибкость, чем пакеты ИМ.

4.Стоимость универсального ПО обычно ниже стоимости па­кета ИМ, хотя не всегда ниже общей стоимости проекта.

Таким образом, поскольку применение обоих методов имеет определенные преимущества, разработчику моделей следует очень серьезно подходить к выбору каждого из них. Если же выбор сде­лан в пользу пакетов ИМ, по критериям и характеристикам, кото­рые используются при создании модели, можно решить, какой кон­кретно пакет лучше выбрать.

35. Классификация программных средств имитационного моделирования

Пакеты ИМ разделены на два основных типа: языки ИМ и предметно-ориентированные программы моделирования. Языки ИМ являются универсальными. Их использование расширяет воз­можности в процессе моделирования, яо зачастую их применение затруднительно. Программы моделирования ориентированы на ре­шение определенной задачи, в них модель разрабатывается с ис­пользованием графики, диалоговых окон и раскрывающихся ме­ню. Такие программы проще изучать и реализовывать, но они не всегда могут обеспечить достаточную гибкость при ИМ.

В последние годы создатели языков ИМ попытались сделать ПО более простым в употреблении. Для этого они использовали графический подход с применением пиктограмм для построения Модели. Вначале разработчик выбирает пиктограммы с помощью мыши и помещает их в рабочую область. Затем он соединяет пик­тограммы, чтобы обозначить именованные потоки в исследуемой системе. Двойным щелчком мышью на пиктограмме можно вы­вести диалоговое окно, где уточняются параметры для добав­ляемых пиктограмм. Предположим, пиктограмма представляет устройство обслуживания в какой-либо системе, в этом случае диалоговое окно позволяет уточнить информацию о числе парал­лельных устройств обслуживания, распределении времени обслу­живания для каждого из них, о том, может ли устройство прийти в неисправность (если может, то каким образом). В то же время раз­работчики предметно-ориентированных программ моделирования сделали программные средства более гибкими, обеспечив возмож­ность программировать с использованием псевдоязыка. По край­ней мере, в одной программе моделирования сейчас можно изме­нять существующие конструкции и создавать новые. Это привело к тому, что отличия между языками ИМ и программами модели­рования стали менее заметными.

Таким образом, существуют два типа пакетов ИМ. Универ­сальные пакеты предназначены для различных целей, но они мо­гут иметь специальные функции для решения одного конкретного вида задач (например, моделирования производственных систем, систем связи или модернизации технологий производства). К та­ким пакетам можно отнести следующие: АРЕНА, EXTEND и GPSS (США).

Предметно-ориентированные пакеты ИМ используют для ре­шения таких специальных задач, как моделирование работы про­изводственных систем, медицинских учреждений, центров выпол­нения заказов.

Для создания имитационных моделей существуют различные подходы, но, прежде чем переходить к их рассмотрению, отметим некоторые особенности процесса продвижения часов модельного времени. В имитационной модели переменная, обеспечивающая текущее значение времени, называется часами модельного време­ни. При использовании дискретно-событийных имитационных моделей требуется следить за текущим значением модельного времени. При этом также необходим механизм для продвижения модельного времени от одного значения к другому. В случае при­менения универсальных языков единица времени для часов мо­дельного времени явно никогда не устанавливается. К тому же модельное время и время, необходимое для прогона имитацион­ной модели на компьютере, как правило, соотнести невозможно.

Существуют два основных подхода к продвижению часов мо­дельного времени: продвижение времени от события к событию и продвижение времени посредством постоянного шага. Первый подход используется во всех основных имитационных программах большинством разработчиков, создающих модели на уни­версальных языках. С учетом этого, а также того, что второй под­ход является разновидностью первого, в дискретно-событийных моделях, рассматриваемых в этой книге, применяется такой под­ход, как продвижение времени от события к событию. При ис­пользовании этого подхода часы модельного времени в исходном состоянии устанавливаются в положение 0 и определяется время возникновения будущих событий. После этого часы модельного времени переходят на время возникновения ближайшего события; при этом состояние системы с учетом происшедшего события, а также сведения о времени появления будущих событий обновля­ются. Затем часы модельного времени продвигаются ко времени возникновения следующего (нового) ближайшего события, со­стояние системы обновляется, определяется время будущих собы­тий и т. д. Процесс продвижения часов модельного времени от времени возникновения одного события ко времени возникнове­ния другого продолжается до тех пор, пока не будет выполнено какое-либо условие останова, указанное заранее. Поскольку в дис­кретно-событийной имитационной модели все изменения проис­ходят только во время возникновения событий, периоды бездейст­вия системы просто пропускаются, и часы переводятся со времени возникновения одного события на время возникновения другого. (При продвижении часов модельного времени с постоянным ша­гом такие периоды бездействия не пропускаются, что приводит к большим затратам компьютерного времени.) Следует отметить, что длительность интервала продвижения часов модельного вре­мени от одного события к другому может быть различной.

36. Возможности при использовании программ имитационного моделирования

При выборе программных средств ИМ следует учитывать все имеющиеся в случае их использования возможности:

• быстродействие, объем памяти и др.;

• совместимость оборудования и ПО;

• анимацию;

• средства получения и обработки статистических данных;

• услуги, предоставляемые заказчикам, и документацию;

• отчеты с выходными данными и графиками.

Самым важным свойством, которым должен обладать про­граммный продукт ИМ, является гибкость, т. е. возможность мо­делировать системы с различным уровнем сложности технологи­ческих процессов. Поскольку двух полностью идентичных систем не существует, пакет ИМ, в котором применяется фиксированное число моделирующих конструкций и нет возможности програм­мирования, для некоторых систем, несомненно, окажется непри­годным. В идеале должна быть возможность моделирования лю­бой системы с использованием только имеющегося программного пакета без применения программ, написанных на каком-либо дру­гом языке. Некоторые возможности ПО, придающие гибкость про­граммному продукту ИМ, перечислены ниже:

• определять и изменять атрибуты объектов и основных пере­менных, а также применять их в логике решений (например, кон­струкции if.. .then., .else);

• использовать математические выражения и функции (лога­рифмирование, возведение в степень и т. п.);

• создавать новые моделирующие конструкции и изменять уже существующие, а также применять их в модифицированном виде.

Следующим важным свойством средств ИМ является простота в применении; многие современные пакеты моделирования снаб­жены графическим интерфейсом пользователя. В таких пакетах должны быть моделирующие конструктивные элементы (напри­мер, пиктограммы или блоки), не слишком примитивные, но и не слишком сложные. В первом случае понадобится очень много конструктивных элементов для моделирования даже достаточно простой ситуации; во втором же случае диалоговое окно каждого такого элемента будет содержать слишком большое число пара­метров, необходимых для обеспечения соответствующей гибкости программы. Управлять такими параметрами можно с помощью вкладок в диалоговых окнах.

При исследовании сложных систем может оказаться целесо­образным иерархическое моделирование. Использование иерархии позволяет сгруппировать несколько основных конструктивных элементов в новые структурные элементы более высокого уровня. В дальнейшем эти элементы можно объединить в структурные элементы еще более высокого уровня и т. д. Последние структурные элементы помещают в библиотеку доступных структурных элементов для их повторного использования. Повторное применение частей модели с расширением логических возможностей позволя­ет повысить эффективность моделирования. Иерархия является важной концепцией многих пакетов моделирования. Ее использо­вание также дает возможность избежать неясностей на экране в графически ориентированных моделях, состоящих из множества пиктограмм и блоков.

Программное обеспечение должно быть снабжено такими средствами отладки, как интерактивный отладчик. Использование мощного отладчика позволяет:

• отслеживать отдельные объекты по всей модели, чтобы убе­диться в правильности их обработки;

• проверить состояние модели при каждом возникновении не­которого события (например, при поломке станка);

устанавливать значения определенных переменных для про­движения событий до конца по логическому пути, встречающему­ся с малой вероятностью.

При моделировании некоторых систем очень важное значение имеет высокая скорость работы модели. В первую очередь это касается моделей военных систем и моделей, тогда требуется об­рабатывать большое количество событий (например, модель быст­родействующей сети связи). Для использования имитационной модели кем-либо, кроме разработчика, желательно, чтобы имелась возможность создания такого интерфейса, с помощью которого неспециалист смог бы легко ввести параметры ИМ.

61