Тема: Теория игр и принятия решений.

Теория игр – это математическая модель теории конфликтных ситуаций, занимается принятием решений в этих ситуациях двумя и более противниками, каждый из которых стремится оптимизировать свои решения за счёт других.

Игра – это совокупность правил, определяющих сущность конфликтной ситуации, которые устанавливают:

• Выбор способа действия игроками на каждом этапе игры

• Информацию, которой обладает каждый игрок при выполнении таких выборов

• Плату для каждого игрока после завершения любого этапа игры

Основными понятиями теории игр являются:

• Конфликтующие стороны, называемые игроками

• Одна реализация игры партией и набор её возможных конечных состояний

• Исход игры – выигрыш, ничья или проигрыш

Игрокам известны платежи в виде матрицы 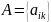. Развитие игры во времени происходит последовательно по этапам (ходам).

Ходом в теории игр называется выбор одного из правил, предусмотренных игрой и его реализации.

Ходы бывают личными и случайными.

Личный ход – сознательный выбор игроком одного из вариантов действия и его осуществление.

Случайный ход – выполняется не волевым решением игрока, а каким- либо способом случайного выбора.

Основным показателем теории игр является совокупность правил, определяющих выбор варианта действия при каждом личном ходе этого игрока от начала до конца игры – стратегия игрока.

Оптимальная стратегия игрока – это стратегия, которая при многократном проведении игры обеспечивает игроку максимальный средний выигрыш или минимально возможный средний проигрыш.

В зависимости от причин, вызывающих неопределённость исходов игры их делят на основные группы:

1. Комбинированные игры, в которых правила позволяют каждому игроку проанализировать все разнообразные ходы и выбрать тот из них, который ведёт к лучшему исходу для этого игрока.

2. Азартные игры – это игры, источником неопределённости которых является случайные факторы. При их анализе применяется теория вероятностей.

3. Стратегические игры – это игры, в которых неопределённость исхода вызвана тем, что каждый из игроков, принимая решение о выборе предстоящего хода, не знает какой стратегии будут придерживаться другие участники игры. Такие игры и изучает теория игр.

В игре могут сталкиваться интересы двух или более игроков. Если в игре участвуют два игрока – игра называется парной, если больше двух – множественной.

Также игры различают по сумме выигрыша:

1. С нулевой суммой (один игрок выигрывает за счёт другого, а сумма выигрыша одного равна сумме проигрыша другого)

2. Парная с нулевой суммой называется антагонистической, так как интересы игроков прямо противоположны.

В зависимости от количества возможных стратегий:

• Конечные – если у каждого игрока имеется только конечное число стратегий.

• Бесконечные – если хотя бы у одного игрока имеется бесконечное число стратегий.

§2. Постановка игровых задач.

Основными вопросами теории игр являются:

1. Какие свойства стратегий следует считать признаками оптимальности.

2. Существуют ли стратегии игроков, которые обладали бы свойствами оптимальности.

3. Как определить оптимальные стратегии, если они существуют.

Пример

Рассмотрим игру двух лиц с нулевой суммой. Пусть игра состоит из двух ходов. Игрок 1 выбирает стратегию , игрок 2 – стратегию ; выигрыш соответственно 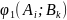и .

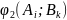Игра каждого из игроков удовлетворяет условиям:

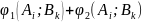=0. Если

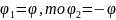
Пусть функция .

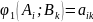Составим матрицу А:

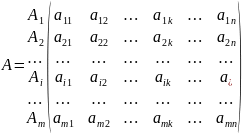
Строки матрицы А соответствуют стратегии , столбцы- стратегии . Матрица А называется платёжной или матрицей игры.

Элемент платёжной матрицы А является выигрышем игрока 1, если он выбрал стратегию , а второй игрок выбрал стратегию . Эти стратегии называются чистыми стратегиями игроков.

Пусть игрок 1 выбирает некую стратегию (игроку 2 известен выбор), тогда в худшем случае он получит выигрыш, равный минимуму , то есть минимальному элементу в i-ой строке платежной матрицы А.

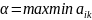
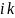
Величина 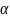называется нижней ценой игры, которая обеспечивает максимальный выигрыш игрока 1, а стратегия , которая обеспечивает получение такого выигрыша, называется максимальной.

Игрок 2 при выборе стратегии проигрывает не более максимального значения из элементов k-го столбца, то есть величина проигрыша не больше максимума . Игрок 2 выбирает такую величину, которая минимизирует максимальный проигрыш.

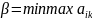
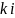
Величина β называется верхней ценой игры, а стратегия – минимаксной.

Пусть выигрыш игрока 1 будет V, тогда его значение ограничено верхней и нижней ценами игры:

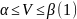
Если же 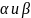совпадают, то выигрыш игрока 1 составляет определённую величину, игра называется вполне определённой.

А выигрыш 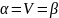называется значением игры и равен элементу . Вполне определённые игры называются также играми с седловой точкой или играми в чистых стратегиях.

Элемент в платёжной матрице А является одновременно минимальным в строке и максимальным в столбце и называется седловой точкой.

Седловой точке соответствуют оптимальные стратегии игроков, а их совокупность является решением игры. Решение игры показывает, что если один из игроков принимает свою оптимальную стратегию, то для другого игрока отклонение от оптимальной стратегии не является выгодным.