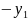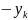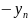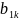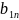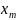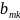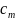- •§1. Экономико-математические методы и моделирование
- •§2. Линейное программирование
- •§3. Графический метод
- •§4.Аналитический метод решения задач линейного программирования
- •§5. Определение опорного решения задачи линейного программирования симплекс методом.
- •§6. Определение оптимального решения задач линейного программирования.
- •Тема: Решение транспортной задачи
- •§1. Постановка задачи и ее математическая модель
- •§2. Построение опорного плана
- •§3. Методы оптимального решения транспортной задачи.
- •§4. Открытые модели транспортных задач
- •§5. Распределительный метод решения транспортных задач
- •§6. Венгерский метод решения транспортной задачи
- •Тема: Целочисленное программирование
- •Тема: Теория игр и принятия решений.
- •§2. Постановка игровых задач.
- •§3. Игра в смешанных стратегиях
- •§4. Элементы теории графов
§6. Венгерский метод решения транспортной задачи
При
решении задачи данным методом
осуществляется последовательный переход
от некоторого недопустимого плана, то
есть не все запасы перевезены от
поставщика потребителям, к допустимому,
который является допустимым планом
решения задач. Этот переход осуществляется
за конечное число итераций. При заполнении
таблицы в них включаются как тарифы
( ),
так и величины перевозимых грузов (
),
а также запасы поставщика (
)
и значения заявок потребителя (
).
),
так и величины перевозимых грузов (
),
а также запасы поставщика (
)
и значения заявок потребителя (
).
Тема: Целочисленное программирование
Целочисленным программированием называется радел математического программирования, изучающий экстремальные задачи, в которых искомые переменные должны иметь целые неотрицательные значения, то есть решение линейных задач необходимо получить в целых числах.
Основным методом, позволяющим найти целочисленное решение за конечное число шагов является метод отсечения плоскостей (метод Гомори).
Сущность метода заключается в том, что задача решается без условия целочисленности, то есть в случае целых значений переменных задача решена. В противном случае к ограничениям задачи добавляют дополнительные ограничения. Это ограничение уменьшает многогранник решений задач, отсекая его часть, и не исключает из него целочисленных точек, кроме того оно обязательно должно быть линейным.
Алгоритм Гомори основан на симплексном методе и содержит следующие этапы решения задач:
Задача линейного программирования решается без учета целочисленности симплексным методом. Если все элементы оптимального плана целые числа, то задача решена.
Если среди элементов оптимального решения имеются не целые числа, то следует выбрать элемент с наибольшей дробной частью и составить дополнительное ограничение (сечение), которое исключает нецелочисленные решения. Дополнительное ограничение составляется в том случае, если базисная переменная в оптимальном плане
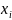 - дробное число, и некоторые коэффициенты
в этой строке симплексной таблицы также
дробные числа. Если эти коэффициенты
являются целыми числами, то такая задача
целочисленного решения не имеет.
- дробное число, и некоторые коэффициенты
в этой строке симплексной таблицы также
дробные числа. Если эти коэффициенты
являются целыми числами, то такая задача
целочисленного решения не имеет.Дополнительные ограничения включаются в симплексную таблицу для оптимального решения. Так как составленный план не будет опорным, то при решении применяют модифицированные жордановы исключения, выбирая разрешающий элемент оп правилу для решения задач двойственным симплекс-методом.
Постановка задачи целочисленного программирования состоит в следующем:
Z
=
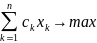 (1)
(1)
При ограничениях неравенств:
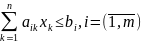 (2)
(2)
При условиях:
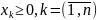 (3)
(3)
Симплексная таблица:
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Σ |
|
|
|
|
|
Q |
Составляем дополнительное ограничение:
Пусть не является целым числом
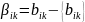 =
=