§5. Определение опорного решения задачи линейного программирования симплекс методом.

Независимые переменные, на знаки которых наложены ограничения называются несвободными, а переменные, не имеющие таких ограничений, называются свободными.

Пусть в таблице (6) §4 после шага модифицированного жорданового исключения все свободные члены 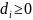, то есть неотрицательные, в этом случае получено одно из опорных решений задачи.

Если же в таблице (6) имеется хотя бы один отрицательный свободный член 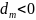, то получаемый план не является опорным.

Для определения опорного плана выполняется шаг модифицированного жорданового исключения, что соответствует переходу от одной вершины многогранника решений к соседней.

Разрешающий элемент симплексной таблицы выбирается по правилу:

1. Отыскивается строка с отрицательным свободным членом, если их несколько, то выбирается строка с наибольшим по модулю отрицательным свободным членом. Если среди коэффициентов взятой строки нет отрицательных, то система №2 несовместна.

2. Если в рассматриваемой строке имеются отрицательные коэффициенты, то выбирается любой из них (обычно наибольший по абсолютной величине) и столбец с этим коэффициентом принимается за разрешающий.

3. При выборе разрешающей строки вычисляются все неотрицательные отношения значений свободных членов к соответствующим коэффициентам разрешающего столбца. Определяются наименьшие и принимается соответствующая строка в качестве разрешающей, а коэффициент, стоящий в знаменателе этого отношения – за разрешающий элемент.

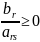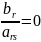Например, таким отношением пусть будет , тогда разрешающим элементом будет , а если , то в качестве разрешающего принимается положительный элемент матрицы .

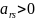§6. Определение оптимального решения задач линейного программирования.

После получения опорного плана решения задач линейного программирования переходим к определению оптимального решения.

Оптимальное решение – это решение, при котором целевая линейная функция принимает экстремальные значения – минимальное или максимальное.

Условием оптимальности при отыскании максимального значения целевой функции симплекс-методом является отсутствие отрицательных коэффициентов в Z-ой строке симплексной таблицы, то есть все свободные члены в симплексной таблице неотрицательные. В Z-ой строке, кроме свободного члена, все коэффициенты при переменных также неотрицательны и полученное решение является опорным и оптимальным.

Если же в Z-ой строке имеется отрицательный коэффициент, то полученное решение не будет оптимальным.

Симплекс-метод определения оптимального решения означает переход от одной вершины многогранника решений к соседней этого многогранника, в которой значение целевой функции Z больше или не меньше чем в исходной вершине. Для осуществления такого перехода выполняется шаг модифицированного жорданового исключения. В симплексной таблице разрешающий столбец определяется вводимой переменной, а разрешающую строку предполагают исключаемой переменной.

Элемент, находящийся на пересечении разрешающей строки и разрешающего столбца, называют ведущим или разрешающим.

Если в Z-ой строке симплексной таблицы имеется несколько отрицательных коэффициентов, то в качестве разрешающего столбца выбираем наибольший по модулю отрицательный элемент этой строки. В разрешающем столбце выбираем все положительные коэффициенты и делим на них соответствующие свободные члены, из полученных отношений принимаем наименьшее и соответствующую строку считаем разрешающей.

После шага модифицированного жорданового исключения соответствующим разрешающим элементом знак у коэффициента Z-ой строки изменяем на противоположный. Если все коэффициенты этой строки окажутся неотрицательными, то план будет оптимальным и задача решена.

Если же в разрешающем столбце (столбец с отрицательным коэффициентом Z-ой строки) нет положительных коэффициентов, то целевая функция не ограничена сверху и оптимального решения не существует.