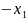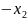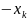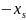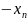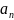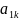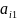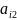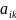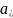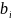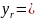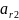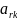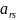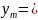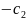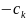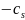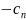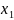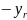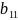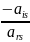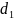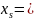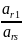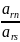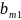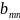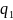§4.Аналитический метод решения задач линейного программирования
Основной метод – симплекс метод.
Симплекс метод – это метод последовательного решения задачи или улучшения плана. Он заключается в определении опорного плана среди решений системы линейных ограничений – неравенств, затем поэтапным переходом к оптимальному решению. Вычислительным аппаратом симплекс метода является модифицированные Жордановы исключения, позволяющие решать задачу линейного программирования в табличной форме.
Пусть основная задача линейного программирования записана
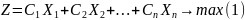
Введём
зависимые переменные, согласно условиям
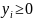и ограничения
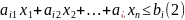
I=(1;m), где m>n и k(1;n)
Перепишем нашу задачу в виде
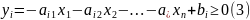
Исходную задачу (1) и (3) перепишем в табличной форме
Таблица (4)
|
|
|
… |
|
… |
|
… |
|
1 |
|
|
|
… |
|
… |
|
… |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
… |
|
… |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
… |
|
… |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
… |
|
… |
|
|
Z= |
|
|
… |
|
… |
|
… |
|
0 |
Один шаг моделированного исключения с разрешающим элементом означает переход к новой таблице (6), которая получается из таблицы (4) по правилам:
зависимая переменная
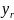и независимая
меняются местами, то есть превращают
зависимые переменные в независимые.разрешающий элемент заменяют на обратную величину
остальные элементы, кроме разрешающего, делятся на разрешающий элемент
остальные элементы разрешающего столбца делятся на отрицательное значение разрешающего элемента, то есть на -
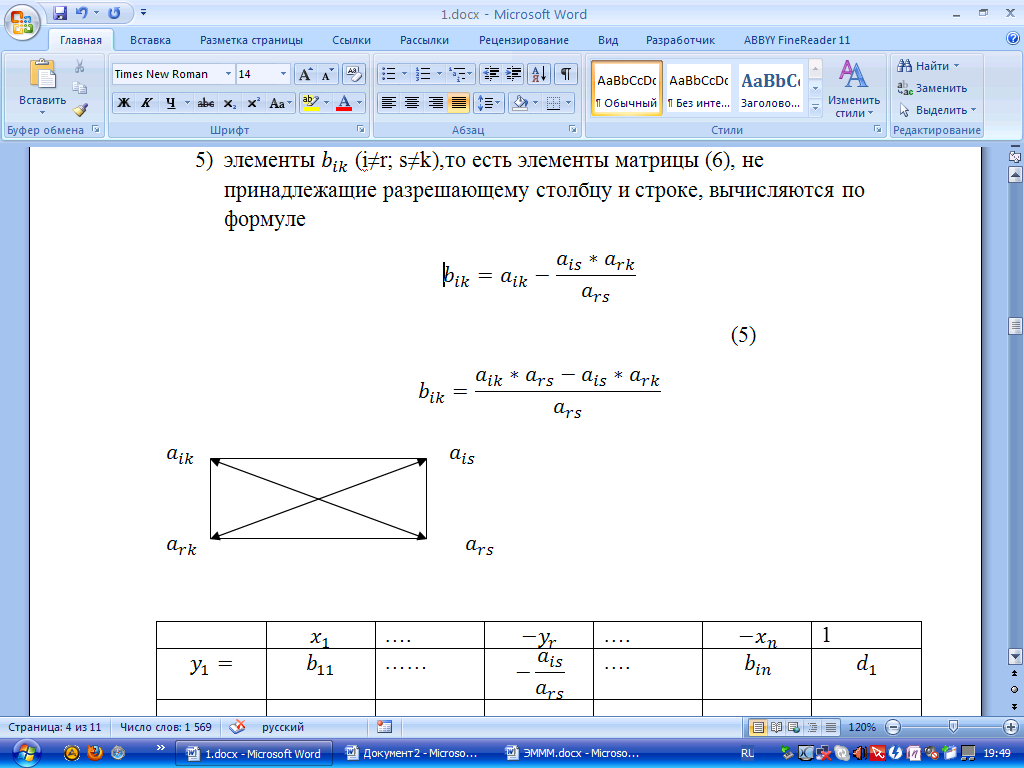
элементы
(i≠r;
s≠k),то
есть элементы матрицы (6), не принадлежащие
разрешающему столбцу и строке, вычисляются
по формуле
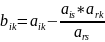
(5)
|
|
…. |
|
…. |
|
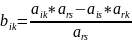
1 |
|
|
…… |
|
…. |
|
|
…. |
…… |
…… |
……. |
…. |
…… |
…… |
|
|
…… |
|
….. |
|
|
….. |
….. |
…… |
…… |
….. |
….. |
….. |
|
|
……. |
|
….. |
|
|
Z= |
|
……. |
|
….. |
|
Q |
Решение задач линейного программирования состоит из 2-ух этапов:
нахождение опорного решения, условием которого является отсутствие отрицательных свободных членов (то есть, чтобы все элементы таблицы (6), расположенные в столбце 1 были неотрицательными)
определение оптимального плана задачи, то есть отыскание экстремальных значений (минимума и максимума) целевой функции. Условием оптимальности при определении максимального значения целевой функции является отсутствие отрицательных коэффициентов в Z –ой строке таблицы (6), кроме свободного члена Q.