САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра машиноведения и деталей машин

Пояснительная записка

Курсовой проект

Расчет узла привода

Выполнил: Студент группы 3032/2 Кривошеев Н.С.

Провеил: Руководитель Гутовский И.Е.

Санкт-Петербург 2010

Cодержание

1.1 Энерго-кинематический расчет узла привода 3

1.2 Расчет косозубой цилиндрической передачи 10

1.2.1 Проектировочный расчет передачи по контактной выносливости зуба 10

1.2.2 Проверочный расчет зубьев на контактную выносливость 18

1.2.3 Проверочный расчет зубьев на изгибную выносливость 21

1.2.4 Проверочный расчет зубчатой передачи при перегрузке 27

1.3 Расчет размеров шестерни прямозубой цилиндрической передачи 30

1.4 Расчет и проектирование промежуточного вала 34

1.4.1 Проектировочный расчет вала 34

1.4.2 Выбор и проверочный расчет подшипников качения 35

1.5 Проверочный расчет шпоночных соединений 43

1.6 Проверочный расчет промежуточного вала 45

Литература 48

1.1 Энерго-кинематический расчет узла привода

Задачей раздела является расчет моментов, частот вращения, мощностей на всех валах привода и передаточных чисел для быстроходной и тихоходной передач.

Кинематическая схема узла привода

Рис.1.1.

| - входной (быстроходный) вал; | | - промежуточный вал; | | | - выходной (тихоходный) вал; 1, 3 - шестерни; 2, 4 - зубчатые колеса; 1-2 - быстроходная передача, 3-4 - тихоходная передача.

Известно, что мощность может быть определена по формуле

N = T·w, (1.1)

Где N - мощность, Вт; T - вращающий момент, Н·м; w - угловая скорость, рад/с. Угловая скорость может быть определена по формуле

(1.2)

где n - частота вращения, об/мин.

Угловая скорость на выходном вале определяется по формуле

(1.3)

где w₃ - угловая скорость на тихоходном валу, рад/с; n_{3 -} частота вращения тихоходного вала, об/мин.

n₃=75 об/мин (из технического задания)

Подставляя численные значения в выражение (1.3), найдем угловую скорость на тихоходном валу

Мощность на выходном вале может быть определена по формуле

N₃=T₃·w₃, (1.4)

Где N₃ - мощность на тихоходном вале, Вт; T₃ - вращающий момент на тихоходном вале, Н·м. Подставляя численные значения в выражение (1.4), получим значение мощности на тихоходном вале

N₃=2250·7,85=17,6 кВт.

Запишем выражение для общего КПД

(1.5)

h_общ - общий коэффициент полезного действия; N₁ - мощность на входном валу, Вт.

Выражая из формулы (1.5) N₁, получим

(1.6)

Запишем формулу для общего КПД

(1.7)

где h_{ПК1 -} КПД подшипника качения на входном валу; h_ЗПБ - КПД быстроходной зубчатой передачи; h_ПК2 - КПД подшипника качения на промежуточном валу; h_ЗПТ - КПД тихоходной зубчатой передачи; h_ПК3 - КПД подшипника качения на выходном валу.

Выбираем h_ПК1=h_ПК2=h_ПК3 =0,99; для зубчатой передачи в закрытом корпусе с цилиндрическими колесами h_ЗПБ=0,98; для открытой зубчатой передачи h_ЗПТ=0,96.

Подставляя численные значения в выражение (1.7), получим величину общего КПД

h_общ=0,99·0,98·0,99·0,96·0,99=0,913.

Подставляя численные значения в выражение (1.6), получим величину мощности на входном валу

Угловую скорость на входном валу можно определить по формуле

(1.8)

где n₁ - частота вращения входного вала, об/мин.

Подставляя численные значения в выражение (1.8), найдем величину угловой скорости на входном валу

Вращающий момент на входном валу определим по формуле

(1.9)

где T₁ - вращающий момент на входном валу, Н·м. Подставляя численные значения, получаем

Запишем формулу для мощности на промежуточном валу

N₂=N₁·h_ПК1·h_ЗПБ, (1.10)

где N₂ - мощность на промежуточном валу, Вт.

Подставляя численные значения в выражение (1.10), найдем величину мощности на промежуточном валу

N₂=19300·0,99·0,98=18,8 кВт.

Введем коэффициент

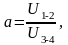(1.11)

где U_1-2 - передаточное число быстроходной передачи; U_{3-4 -} передаточное число тихоходной передачи.

Запишем выражение для общего передаточного числа

U_общ= U_1-2·U_3-4, (1.12)

где U_общ - общее передаточное число.

Запишем формулу для U_общ

(1.13)

Подставляя численные значения в выражение (1.13), найдем U_общ

Выражая из формул (1.11) и (1.12) передаточное число тихоходной передачи, получаем

(1.14)

Подставляя численные значения в выражение (1.14), получаем

Выражая из формулы (1.12) передаточное число быстроходной передачи, получаем

(1.15)

Подставляя численные значения в формулу (1.15), получаем

Частоту вращения промежуточного вала определим по формуле

(1.16)

где n₂ - частота вращения промежуточного вала, об/мин. Подставляя численные значения в формулу (1.16), получаем

Угловая скорость на промежуточном валу определяется по формуле

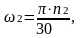(1.17)

где w₂ - угловая скорость на промежуточном валу, рад/с.

Подставляя численные значения в формулу (1.17), получаем

Вращающий момент на промежуточном валу определим по формуле

(1.18)

где T_{2 -} вращающий момент на промежуточном валу, Н·м.

Подставляя численные значения в выражение (1.18), получаем

Результаты всех вычислений сведем в таблицу

Таблица 1.1.

Результаты энерго-кинематического расчета

Вал	U	T, Н·м	n, об/мин	N, Вт
|	4,2	185	1000	19300
| |		752	238	18800
	3,2
| | |		2250	95	17600