3. Анализ алгоритма решения задачи

3.1 Метод Монте-Карло

Для вычисления площади четырехугольника необходимо вычислить площадь прямоугольника, описывающего заданный четырехугольник, а затем N раз сгенерировать по два случайных числа для координат x и y, соответствующих координатам сгенерированной точки.

Для каждой точки выполняется проверка, попала ли точка внутрь заданного четырехугольника. Если из N точек M точек оказалось внутри четырехугольника, а площадь прямоугольника равна S, то площадь четырехугольника будет приближенно равна .

Поскольку площадь данного четырехугольника легко вычисляется по правилам геометрии, мы можем определить относительную погрешность приближенного вычисления этой площади методом Монте-Карло. Естественно, чем больше N, тем меньше должна быть погрешность такого вычисления.

Данный четырехугольник является трапецией. Для вычисления площади трапеции по правилам геометрии используется формула:

,

где ae и bc – длина нижнего и верхнего основания трапеции соответственно, а h – высота трапеции. Длина основания вычисляется как разность между абсциссами точек e_x-a_x и c_x-b_x. Высота трапеции определяется как разность между ординатами точек b_y-a_y.

3.2 Определение попадания точки внутрь трапеции

Предположим, мы задали координаты 4 вершин трапеции abce. Точка с координатами (x;y) лежит внутри трапеции abce, если она лежит справа или на прямой, проходящей через точки a и b, и слева или на прямой, проходящей через точки с и e (рис. 2).

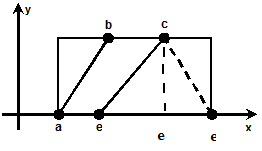
Рис. 2. Определение попадания точки в трапецию

Из исходных данным нам известно, что возможных расположений точки е относительно точки c может быть 3 – xc<xe, xc>xe, xc=xe . Это отображено на рис.2. Определим теперь алгоритм определения принадлежности точки прямой.

В математике прямую можно задать с помощью уравнения прямой y=k*x + b, где х, у – это координаты точки, k – тангенс угла или , который можно определить, как отношение катетов противолежащего и прилежащего угла, если рассмотреть треугольник, составленный из 3 точек. Отсюда - 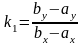. Относительно точки е нам надо учитывать то, возможных вариантов ее расположения может быть3. Коэффициент будет рассчитываться по аналогии - 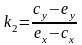, но если xc<xe , то коэффициент поменяет знак. В случае, если xc=xe , нам вообще не потребуется этот коэффициент, мы будем всего лишь сравнивать координату x относительно точки с, так как в этом случае, правой границей будет прямая. b – это смещение относительно начала координат. После нахождения к, мы сможем подставить известные данные в уравнение, и найти b.

Для каждого из трех возможных вариантов расположения абсциссы точки e относительно абсциссы точки c существует свое условие проверки для определения принадлежности точки с координатами (x;y) плоскости, ограниченной трапецией abce.

Если один раз рассчитать угловые коэффициенты (K) и коэффициент смещения (B), а затем подставить координаты генерируемой точки , то получим следующее соотношение:

Требуется отдельно оговорить тот факт, что возможных расположений точки С относительно точки E может быть 3. Система выше верна, если координаты точки c меньше координат точки e.

Если абсцисса точки e меньше абсциссы точки c, то точка с координатами (x;y) лежит внутри трапеции abce тогда, когда одновременно выполняются условия:

Если абсцисса точки e равна абсциссе точки c, то точка с координатами (x;y) лежит внутри трапеции abce тогда, когда выполняется условие:

#tyt bidet shema

Рис. 3. Определение попадания точки внутрь трапеции. Схема алгоритма